







| Bu sayfada üyelere özel yazılar bulunuyor. üye girişi yaparak bu yazıları görüntüleyebilirsiniz.
Burayı tıklayarak üye girişi yapabilirsiniz. Burayı tıklayarak üye olabilirsiniz. |
||
|
|
Matematikte, Eratosthenes (Eratostenes) Kalburu belirli bir tamsayıya kadar yer alan asal sayıların bulunması için kullanılan bir yöntemdir. Daha hızlı ve karmaşık olan Atkin kalburunun atası sayılır. Eski Yunan'da Eratosten tarafından geliştirilmiştir.

İki sayı arasındaki asal sayıları bulmak için bu yöntem oldukça kullanışlı. Çalışması biraz yavaş olsa da (diğer formüllere göre) yine de eğlenceli ve sonuçta diğerlerinden daha az karmaşık.
Kullanımı:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
1′e asal sayı olmadığı için çarpı işareti koyun.
2′yi bir asal sayı olduğu için daire içine alın, daha sonra 2′nin tüm katlarına çarpı işareti koyun.
3′ü de daire içine alın ve katlarına da çarpı işareti koyun.
Ondan büyük olan 5′e daire ve katlarına da çarpı işareti koyun.
100′e kadar olan tüm sayılara bu işlemi uygularsanız, 100′e kadar olan asal sayıları bulursunuz.

Bulduğunuz asallarla 1000′e kadar olanları, onlarla 1.000.000′a kadar olanları da bulursunuz ve bu sonsuza kadar gider.
Bu yönteme Eratosthenes’ in Kalburu denir.
Eratosthenes kimdir?
Eratosthenes (Eratosten) (Yunanca Ἐρατοσθένης) (M.Ö. 276-M.Ö. 194)Yunanlı matematikçi , coğrafyacı ve astronom.
Eratosthenes, Cyrene’de (günümüz Libya’sı) doğmuştur, ama ölene kadar tüm yaşamı Ptolemaios soyunun hüküm sürdüğü Mısır’ın başkenti Alexandria’da (İskenderiye) geçmiştir. Hiç evlenmemiştir.
Eratosthenes Alexandria’da ve bir müddet Atina’da öğrenim görmüştür. İ.Ö.236′da Ptolemaios III Euergetes I tarafından Alexandria Kütüphanesi’ne, o koltuktaki ilk kütüphaneci Zenodotos’un ardından, kütüphaneci olarak atanmıştır.
Matematik ve doğal bilimlere katkılarda bulunmuştur. İ.Ö.195 de kör olmuştur ve bir yıl sonra kasıtlı olarak kendini aç bırakarak ölmüştür.
Meridyen yayının uzunluğunu ve ondan yararlanarak Dünya’nın çevre uzunluğunu Ekvator’u hesaplamış, çalışmalarını Geopraphika adlı eserinde toplamıştır.
Dünya üzerindeki yerleşik alanların sınırlarını, hazırladığı bir haritada da gösteren matematik coğrafyacıdır.
Kaynak: Wikipedia.org
Altın Oran Nedir?
"...Eğer uygulama veya işlev unsurları açısından hoşa giden ya da son derece dengeli olan bir forma ulaşılmışsa, orada Altın Sayı'nın bir fonksiyonunu arayabiliriz... Altın Sayı, matematiksel hayal gücünün değil de, denge yasalarına ilişkin doğal prensibin bir ürünüdür."1

Mısır'daki piramitler, Leonardo da Vinci'nin Mona Lisa adlı tablosu, ay çiçeği, salyangoz, çam kozalağı ve parmaklarınız arasındaki ortak özellik nedir?

Bu sorunun cevabı, Fibonacci isimli İtalyan matematikçinin bulduğu bir dizi sayıda gizlidir. Fibonacci sayıları olarak da adlandırılan bu sayıların özelliği, dizideki sayılardan her birinin, kendisinden önce gelen iki sayının toplamından oluşmasıdır. 2
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ... |
Fibonacci sayılarının ilginç bir özelliği vardır. Dizideki bir sayıyı kendinden önceki sayıya böldüğünüzde birbirine çok yakın sayılar elde edersiniz. Hatta serideki 13. sırada yer alan sayıdan sonra bu sayı) sabitlenir. İşte bu sayı "altın oran" olarak adlandırılır.
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618
987 / 610 = 1,618
1597 / 987 = 1,618
2584 / 1597 = 1,618
İnsan Vücudu ve Altın Oran
Sanatçılar, bilim adamları ve tasarımcılar, araştırmalarını yaparken ya da ürünlerini ortaya koyarlarken orantıları altın orana göre belirlenmiş insan bedenini ölçü olarak alırlar. Leonardo da Vinci ve Corbusier tasarımlarını yaparken altın orana göre belirlenmiş insan vücudunu ölçü almışlardır. Günümüz mimarlarının en önemli başvuru kitaplarından biri olan Neufert'te de altın orana göre belirlenmiş insan vücudu temel alınmaktadır.
İnsan Bedeninde Altın Oran
Bedenin çeşitli kısımları arasında var olduğu öne sürülen ve yaklaşık altın oran değerlerine uyan "ideal" orantı ilişkileri genel olarak bir şema halinde gösterilebilir.3
Aşağıdaki şemada yer alan M/m oranı her zaman altın orana denktir: M/m=1,618
İnsan vücudunda altın orana verilebilecek ilk örnek; göbek ile ayak arasındaki mesafe 1 birim olarak kabul edildiğinde, insan boyunun 1,618'e denk gelmesidir. Bunun dışında vücudumuzda yer alan diğer bazı altın oranlar şöyledir:
Parmak ucu-dirsek arası / El bileği-dirsek arası,
Omuz hizasından baş ucuna olan mesafe / Kafa boyu,
Göbek-baş ucu arası mesafe / Omuz hizasından baş ucuna olan mesafe,
Göbek-diz arası / Diz-ayak ucu arası.
İnsan Eli
Elinizi derginin sayfasından çekip ve işaret parmağınızın şekline bir bakın. Muhtemelen orada da altın orana şahit olacaksınız.
Parmaklarımız üç boğumludur. Parmağın tam boyunun İlk iki boğuma oranı altın oranı verir (baş parmak dışındaki parmaklar için). Ayrıca orta parmağın serçe parmağına oranında da altın oran olduğunu fark edebilirsiniz.4
2 eliniz var, iki elinizdeki parmaklar 3 bölümden oluşur. Her elinizde 5 parmak vardır ve bunlardan sadece 8'i altın orana göre boğumlanmıştır. 2, 3, 5 ve 8 fibonocci sayılarına uyar.
İnsan Yüzünde Altın Oran
İnsan yüzünde de birçok altın oran vardır. Ancak bunu elinize hemen bir cetvel alıp insanların yüzünde ölçüler almayı denemeyin. Çünkü bu oranlandırma, bilim adamları ve sanatkarların beraberce kabul ettikleri "ideal bir insan yüzü" için geçerlidir.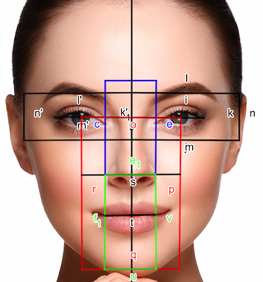
Örneğin üst çenedeki ön iki dişin enlerinin toplamının boylarına oranı altın oranı verir. İlk dişin genişliğinin merkezden ikinci dişe oranı da altın orana dayanır. Bunlar bir dişçinin dikkate alabileceği en ideal oranlardır. Bunların dışında insan yüzünde yer alan diğer bazı altın oranlar şöyledir:
Yüzün boyu / Yüzün genişliği,
Dudak- kaşların birleşim yeri arası / Burun boyu,
Yüzün boyu / Çene ucu-kaşların birleşim yeri arası,
Ağız boyu / Burun genişliği,
Burun genişliği / Burun delikleri arası,
Göz bebekleri arası / Kaşlar arası.
Akciğerlerdeki Altın Oran
Amerikalı fizikçi B. J. West ile doktor A. L. Goldberger, 1985-1987 yılları arasında yürüttükleri araştırmalarında 5, akciğerlerin yapısındaki altın oranının varlığını ortaya koydular. Akciğeri oluşturan bronş ağacının bir özelliği, asimetrik olmasıdır. Örneğin, soluk borusu, biri uzun (sol) ve diğeri de kısa (sağ) olmak üzere iki ana bronşa ayrılır. Ve bu asimetrik bölünme, bronşların ardışık dallanmalarında da sürüp gider.6 İşte bu bölünmelerin hepsinde kısa bronşun uzun bronşa olan oranının yaklaşık olarak 1/ 1,618 değerini verdiği saptanmıştır.
Altın Dikdörtgen ve Sarmallardaki Tasarım
Kenarlarının oranı altın orana eşit olan bir dikdörtgene "altın dikdörtgen" denir. Uzun kenarı 1,618 birim kısa kenarı 1 birim olan bir dikdörtgen altın dikdörtgendir. Bu dikdörtgenin kısa kenarının tamamını kenar kabul eden bir kare ve hemen ardından karenin iki köşesi arasında bir çeyrek çember çizelim. Kare çizildikten sonra yanda kalan küçük bir kare ve çeyrek çember çizip bunu asıl dikdörtgenin içinde kalan tüm dikdörtgenler için yapalım. Bunu yaptığınızda karşınıza bir sarmal çıkacaktır.
İngiliz estetikçi William Charlton insanların sarmalları hoş bulmaları ve binlerce yıl öncesinden beri kullanmalarını "Sarmallardan hoşlanırız çünkü, sarmalları görsel olarak kolayca izleyebiliriz." 7 diyerek açıklar.
Temelinde altın oranı yatan sarmallar doğada şahit olabileceğiniz en eşsiz tasarımları da barındırırlar. Ayçiçeği ya da kozalak üzerindeki sarmal dizilimler bu konuda verilebilecek ilk örneklerdir. Yüce Allah'ın kusursuz yaratışının ve her varlığı bir ölçü ile yarattığının bir örneği olan bu durumun yanı sıra birçok canlı büyüme sürecini de logaritmik sarmal formunda gerçekleştirir. Bunun sarmaldaki yayların daima aynı biçimde olması ve yayların büyüklüğünün değişmesine karşın esas şeklin (sarmal) hiç değişmemesidir. Matematikte bu özelliğe sahip başka bir şekil yoktur.8
Deniz Kabuklarındaki Tasarım
Bilim adamları deniz dibinde yaşayan ve yumuşakça olarak sınıflandırılan canlıların taşıdıkları kabukların yapısını incelerken bunların formu, iç ve dış yüzeylerinin yapısı dikkatlerini çekmiştir:
"İç yüzey pürüzsüz, dış yüzeyde yivliydi. Yumuşakça kabuğun içindeydi ve kabukların iç yüzeyi pürüzsüz olmalıydı. Kabuğun dış köşeleri kabukların sertliğini artırıyor ve böylelikle, gücünü yükseltiyordu. Kabuk formları yaratılışlarında kullanılan mükemmellik ve faydalarıyla hayrete düşürür. Kabuklardaki spiral fikir mükemmel geometrik formda ve şaşırtıcı güzellikteki 'bilenmiş' tasarımda ifade edilmiştir."9
Yumuşakçaların pek çoğunun sahip olduğu kabuk logaritmik spiral şeklinde büyür. Bu canlıların hiçbiri şüphesiz logaritmik spiral bir yana, en basit matematik işleminden bile habersizdir. Peki nasıl olup da söz konusu canlılar kendileri için en ideal büyüme tarzının bu şekilde olduğunu bilebiliyorlar? Bazı bilim adamlarının "ilkel" olarak kabul ettiği bu canlılar, bu şeklin kendileri için en ideal form olduğunu nereden bilmektedirler? Böyle bir büyüme şeklinin bir şuur ya da akıl olmadan gerçekleşmesi imkansızdır. Bu şuur ne yumuşakçalarda ne de -bazı bilim adamlarının iddia ettiği gibi- doğanın kendisinde mevcuttur. Böyle bir şeyi tesadüflerle açıklamaya kalkışmak çok büyük bir akılsızlıktır. Bu ancak üstün bir aklın ve ilmin ürünü olacak bir tasarımdır.
Biyolog Sir D'Arcy Thompson uzmanı olduğu bu tür büyümeyi "Gnom tarzı büyüme" olarak adlandırılmıştı. Thompson'ın bu konudaki ifadeleri şöyledir:
"Bir deniz kabuğunun büyüme sürecinde, aynı ve değişmez orantılara bağlı olarak genişlemesi ve uzamasından daha sade bir sistem düşünemeyiz. Kabuk ...giderek büyür, fakat şeklini değiştirmez."10
Birkaç santimetre çapındaki bir nautilusta, gnom tarzı büyümenin en güzel örneklerinden birini görmek mümkündür. C. Morrison insan zekası ile bile planlaması hayli güç olan bu büyüme sürecini şöyle anlatır:
"Nautilus'un kabuğunun içinde, sedef duvarlar ile örülmüş bir sürü odacığın oluşturduğu içsel bir sarmal uzanır. Hayvan büyüdükçe, sarmal kabuğunun ağız kısmında, bir öncekinden daha büyük bir odacık inşa eder ve arkasındaki kapıyı bir sedef tabakası ile örterek daha geniş olan bu yeni bölüme ilerler."11
Kabuklarındaki farklı büyüme oranlarını içeren logaritmik sarmallara göre diğer deniz canlıları bilimsel adlarıyla şöyle sıralanabilir:
Haliotis Parvus, Dolium Perdix, Murex, Fusus Antiquus, Scalari Pretiosa, Solarium Trochleare.
Bugün fosil halinde bulunan ve Amonitlerde logaritmik sarmal şeklinde gelişen kabuklar taşırlar.
Hayvanlar dünyasında sarmal formda büyüme sadece yumuşakçaların kabukları ile sınırlı değildir. Özellikle Antilop, yaban keçisi, koç gibi hayvanların boynuzları gelişimlerini temelini altın orandan alan sarmallar şeklinde tamamlarlar.12
İşitme ve Denge Organında Altın Oran
İnsanın iç kulağında yer alan Cochlea (Salyangoz) ses titreşimlerini aktarma işlevini görür. İçi sıvı dolu olan bu kemiksi yapı, içinde altın oran barındıran _=73 derece 43´ sabit açılı logaritmik sarmal formundadır.
Sarmal Formda Gelişen Boynuzlar ve Dişler
Filler ile soyu tükenen mamutların dişleri, aslanların tırnakları ve papağanların gagalarında logaritmik sarmal kökenli yay parçalarına göre biçimlenmiş örneklere rastlanır. Eperia örümceği de ağını daima logaritmik sarmal şeklinde örer. Mikroorganizmalardan planktonlar arasında, globigerinae, planorbis, vortex, terebra, turitellae ve trochida gibi minicik canlıların hepsinin sarmala göre inşa edilmiş bedenleri vardır.
Mikrodünyada Altın Oran
Geometrik şekiller sadece üçgen, kare veya beşgen, altıgen ile kısıtlı değildir. Bu saydığımız şekiller değişik şekillerde de biraraya gelerek yeni üç boyutlu geometrik şekiller oluşturabilirler. Bu konuda ilk olarak küp ve piramit örnek olarak verilebilir. Ancak bunların dışında, günlük hayatta hiç karşılaşmadığımız hatta ismini dahi ilk defa duyduğumuz tetrahedron (düzgün dört yüzlü), oktahedron, dodekahedron ve ikosahedron gibi üç boyutlu şekillerde vardır. Dodekahadron 13 tane beşgenden, ikosahedron ise 20 adet üçgenden oluşur. Bilim adamları bu şekilleri matematiksel olarak birbirine dönüşebileceğini ve bu dönüşümün altın orana bağlı oranlarla gerçekleştiğini bulmuşlardır.
 | 16. Yüzyılda altın oran için “hazine” ifadesini kullanan Kepler, beş düzgün cisim arasındaki geometrik dönüşümlere çok önem vermiş ve gezegenlerin yörüngeleri ile bu cisimleri çevreleyen küreler arasında bir ba¤lantı kurmaya çalışmıştır. Kepler, düzgün çok yüzlüleri iç içe geçmiş şekilde gösteren ve bu düzen ile Güneş Sistemi arasındaki bağlantıyı araştıran şemalar geliştirmiştir. (J. A. West & J. G. Toonder, The Case for Astrology, Penguin Books, 1970) |
Miroorganizmalarda altın oran barındıran üç boyutlu formlar oldukça yaygındır. Birçok virüs ikosahedron yapısında bir biçime sahiptir. Bunların en ünlüsü Adeno virüsüdür. Adeno virüsünün protein kılıfı, 252 adet protein alt biriminin düzenli bir biçimde dizilmesi ile oluşur. İkosahedronun köşelerinde yer alan 12 alt birim ise beşgen prizmalar biçimdedir. Bu köşelerden diken benzeri yapılar uzanır.
Virüslerin altın oranları bünyesinde barındıran formlarda olduğunu tespit eden ilk kişi 1950'li yıllarda Londra'daki Birkbeck Koleji'nden A. Klug ile D. Caspar'dır.13 Üzerinde ilk tespit yapılan virüs ise Polyo virüsüdür. Rhino 14 virüsü de Polyo virüsü ile aynı formu gösterir.
Peki acaba virüsler neden biz insanların zihnimizde canlandırmasını bile zorlukla yapabildiğimiz, böyle altın orana dayalı özel bir formlara sahiptirler? Bu formların kaşifi A. Klug bu konuyu şöyle açıklıyor:
"Caspar ile ben, küresel bir virüs kılıfı için optimum tasarımın ikosahedron tarzı bir simetriye dayandığını gösterdik. Böyle bir düzenleme bağlantılardaki sayıyı en aza indirir... Buckminster Fuller'in yarı küresel jeodezik kubbelerinden14 çoğu da benzer bir geometriye göre inşa edilirler. Bu kubbelerin oldukça ayrıntılı bir şemaya uyularak monte edilmeleri gerekir. Halbuki virüs, bir virüs kılıfı, alt birimlerinin esnekliğinden ötürü kendi kendini inşa eder."15
Klug'un bu açıklaması çok açık bir gerçeği bir kez daha ortaya koymaktadır. Bilim adamlarının "en basit ve en küçük canlı parçalarından biri"16 olarak gördükleri virüslerde bile hassas bir planlama ve akıllı bir tasarım vardır. Bu tasarım, dünyanın önde gelen mimarlarından Buckminster Fuller'ın gerçekleştirdiği tasarımlardan çok daha başarılı ve üstündür.
Dodekahedron ile ikosahedron, tek hücreli deniz yaratıkları olan ışınlıların silisten yapılma iskeletlerinde de ortaya çıkar.
Işınlılar (radiolaria), her köşesinden birer yalancı ayak çıkan düzgün Dodekahedron gibi, bu iki geometrik formdan kaynaklanan yapıları, yüzeylerindeki çok çeşitli oluşumlarla birlikte değişik güzellikteki bedenleri oluştururlar.17
Büyüklükleri bir milimetreden daha küçük olan bu organizmalara örnek olarak, ikosahedron yapılı Circigonia Icosahedra ile dodekahedran iskeletli Circorhegma Dodecahedra'nın adları verilebilir.18
DNA'da Altın Oran
Canlıların tüm fiziksel özelliklerinin depolandığı molekül de altın orana dayandırılmış bir formda yaratılmıştır. yaşam için program olan DNA molekülü altın orana dayanmıştır. DNA düşey doğrultuda iç içe açılmış iki sarmaldan oluşur. Bu sarmallarda her birinin bütün yuvarlağı içindeki uzunluk 34 angström genişliği 21 angström'dür. (1 angström; santimetrenin yüz milyonda biridir) 21 ve 34 art arda gelen iki Fibonacci sayısıdır.
Kar Kristallerinde Altın Oran
Altın oran kristal yapılarda da kendini gösterir. Bunların çoğu gözümüzle göremeyeceğimiz kadar küçük yapıların içindedir. Ancak kar kristali üzerindeki altın oranı gözlerinizle göre bilirsiniz. Kar kristalini oluşturan kısalı uzunlu dallanmalarda, çeşitli uzantıların oranı hep altın oranı verir.19
Uzayda Altın Oran
Evrende, yapısında altın oran barındıran birçok spiral galaksi bulunur.
Fizikte de Altın Oran....
Fibonacci dizileri ve altın oran ile fizik biliminin sahasına giren konularda da karşılaşırız:
"Birbiriyle temas halinde olan iki cam tabakasının üzerine bir ışık tutulduğunda, ışığın bir kısmı öte yana geçer, bir kısmı soğurulur, geriye kalanı da yansır. Meydana gelen, bir, 'çoklu yansıma' olayıdır. Işının tekrar ortaya çıkmadan önce camın içinde izlediği yolların sayısı, ışının maruz kaldığı yansımaların sayısına bağlıdır. Sonuçta, tekrar ortaya çıkan ışın sayılarını belirlediğimizde bunların Fibonacci sayılarına uygun olduğunu anlarız."20
Doğada birbiriyle ilişkisiz canlı veya cansız pek çok yapının belli bir matematik formülüne göre şekillenmiş olması onların özel olarak tasarlanmış olduklarının en açık delillerinden biridir. Altın oran, sanatçıların çok iyi bildikleri ve uyguladıkları bir estetik kuralıdır. Bu orana bağlı kalarak üretilen sanat eserleri estetik mükemmelliği temsil ederler. Sanatçıların taklit ettikleri bu kuralla tasarlanan bitkiler, galaksiler, mikroorganizmalar, kristaller ve canlılar Allah'ın üstün sanatının birer örneğidirler.
1 Mehmet Suat Bergil, Doğada/Bilimde/Sanatta, Altın Oran, Arkeoloji ve Sanat Yayınları, 2.Basım, 1993, s. 155.
2 Guy Murchie, The Seven Mysteries Of Life, First Mariner Boks, New York s. 58-59.
3 J. Cumming, Nucleus: Architecture and Building Construction, Longman, 1985.
4 Mehmet Suat Bergil, Doğada/Bilimde/Sanatta, Altın Oran, Arkeoloji ve Sanat Yayınları, 2.Basım, 1993, s. 87.
5 A. L. Goldberger, et al., "Bronchial Asymmetry and Fibonacci Scaling." Experientia, 41 : 1537, 1985.
6 E. R. Weibel, Morphometry of the Human Lung, Academic Press, 1963.
7 William. Charlton, Aesthetics:An Introduction, Hutchinson University Library, London, 1970.
8 Mehmet Suat Bergil, Doğada/Bilimde/Sanatta, Altın Oran, Arkeoloji ve Sanat Yayınları, 2.Basım, 1993, s. 77.
9 http://www.goldenmuseum.com/index_engl.html
10 D'Arcy Wentworth Thompson, On Growth and Form, C.U.P., Cambridge, 1961.
11 C. Morrison, Along The Track,Withcombe and Tombs, Melbourne,
12 http://www.goldenmuseum.com/index_engl.html
13 J. H. Mogle, et al., "The Stucture and Function of Viruses", Edward Arnold, London, 1978.
14 Buckminster Fuller'in Jeodezik Kubbe tasarımları hakkında ayrıntılı bilgi için bakınız: Teknoloji Doğayı Taklit Ediyor, Biyomimetik, Harun Yahya, Global Yayıncılık, İstanbul.
15 A. Klug "Molecules on Grand Scale", New Scientist, 1561:46, 1987.
16 Mehmet Suat Bergil, Doğada/Bilimde/Sanatta, Altın Oran, Arkeoloji ve Sanat Yayınları, 2.Basım, 1993, s. 82
17 Mehmet Suat Bergil, Doğada/Bilimde/Sanatta, Altın Oran, Arkeoloji ve Sanat Yayınları, 2.Basım, 1993, s. 85
18 Değişik ışınlı bedenleri için bakınız: "H. Weyl, Synnetry, Princeton, 1952.
19 Emre Becer, "Biçimsel Uyumun Matematiksel Kuralı Olarak, Altın Oran", Bilim ve Teknik Dergisi, Ocak 1991, s.16.
20 V.E. Hoggatt, Jr. Ve Bicknell-Johnson, Fibonacci Quartley, 17:118, 1979.
KONULAR :
8. sınıf deneme sınavı sınavları SBS
2012 Töder Sbs Denemesi indirmek için tıklayın
2012 Mayıs Özdebir SBS Denemesini indirmek için tıklayın
Özdebir SBS Denemesi indir
Kaynak: Denemelerin tüm hakları ozdebirsinavlar.com a ait olup ozdebirsinavlar.com örnek deneme sınavıdır. Hiç bir şekilde parayla satılamaz..
Yukarıdaki dökümanları açabilmek için Adobe Reader 'ın 5.0 veya üstü sürümünün sisteminizde yüklü olması gerekmektedir.
Yasal Uyarı İçin tıklayınız.
6. ve 7. Sınıf Öğrencileri için Takdir ve Teşekkür Hesaplama Robotu
6. ve 7. Sınıf Öğrencileri aşağıdaki robotu kullanarak takdir ya da teşekkür hesaplamasını hemen yapabilirler. 6. sınıf takdir teşekkür hesaplama , 7. sınıf takdir teşekkür hesaplama , ders notlarınızı girerken, yanlış girmemeye özen gösteriniz. Türkçe dersinizin notu 55′ten düşük olursa ya da herhangi bir dersiniz 45′in altında olursa hesaplama yapılmaz, çünkü belge alamazsınız. E-okul veli bilgilendirme sisteminde yazan her bir dersin dönem notu ortalamasını girin. 6. 7. ve 8. Sınıf Online Takdir Teşekkür Hesaplama , Takdir Teşekkür Hesaplama 2012 E-okul
TAKDİR yada TEŞEKKÜR belgesi alanlar Facebook sayfamızı beğenin.Bütün Takdir ve teşekkür alan öğrenciler bu sayfada!
Takdir Teşekkür Hesaplama Modülü sonucunun doğruluk payı nedir?
E-okul takdir teşekkür hesaplamasında puanlarınızı küsüratlarla birlikte girdiğinizde e-okul sistemi ile birebir aynı sonucu verir. Eksiği veya fazlası yoktur.
Takdir Teşekkür Hesaplama yaparken 84,99 veya 69.99 gibi küsüratları üste tamamlar mı?
E-okul Takdir Teşekkür sisteminde belge hesaplama işlemlerinde yukarıya yuvarlama yoktur.
Takdir ya da Teşekkür belgesi alabilmek için Türkçe, Edebiyat, Dil anlatım derslerinin ortalaması 55'ten büyük mü olmalıdır?
İlköğretim 4, 5, 6, 7, 8. sınıflarda Türkçe notu 55'ten büyük olmalı, liseler için bu zorunluluk geçerli değil.
Not ortamala küsüratları belge hesaplamada dikkate alınıyor mu?
Not küsüratları teşekkür ya da takdir almada dikkate alınır.
Belge puanım 70'in üstünde ancak zayıfım var belge alabilir miyim?
Takdir ya da teşekkür belgesi alabilmek için notlarınızın 45'ten düşük not olmaması gerekir.
Puanım 85'in üstünde ancak belge alamazsınız diyor!
Not ortalamanız 70 ya da 85'in üzerinde olmasına rağmen belge alamıyorsanız Türkçe ders notunuz 55'ten küçüktür ve yahut 45'ten küçük notunuz olduğu için takdir ya da teşekkür belgesine hak kazanamıyorsunuzdur.
MEB 8. sınıf SBS'ye giren bir öğrencinin sınavdan alacağı yaklaşık puanı hesaplamak için ilgili testlerden yaptığı doğru ve yanlış sayılarını aşağıdaki hesaplama formuna girdikten sonra hesaplama butonuna basınız.
İlköğretimin 6'ıncı sınıflarında öğrencinin derslerden, o yılın müfredatında belirtilen kazanımları elde etme seviyesinin ölçüleceği Milli Eğitim Bakanlığı tarafından her yıl haziran ayında ders yılı bitiminden sonra düzenlenen merkezi sistem sınavından alınan puandır. Bu puan öğrencinin ileriki dönemde liselere girişinde etkili olmaktadır.
Hesaplama.net MEB 8. sınıf SBS puanı hesaplama aracında, 2009 yılında yapılan SBS uygulamasına ait Test Ortalama ve Standart Sapmaları ile maksimum ve minimum Toplam Ağırlıklı Standart Puanlar kullanılarak hesaplamalar yapılmaktadır. Bu nedenle hesaplanan puanlar tahmini olarak öğrencinin alacağı puanı göstermektedir.
| 8 / - MATEMATİK - 2009 ÇIKMIŞ SBS MATEMATİK SORULARI 10/03/2012 |
| 8 / - MATEMATİK - 2010 ÇIKMIŞ SBS MATEMATİK SORULARI 10/03/2012 |
| 8 / - MATEMATİK - 2011 ÇIKMIŞ SBS MATEMATİK SORULARI 10/03/2012 |
>
Ünlü matematikçiler,ünlü türk matematikçileri,matematiğe kazandırdıkları, pisagor, galois,baire,boole,ömer hayyam,cahit arf,...

Milas’lı Thales, Mısır matematik okulunun ilk öğrencisidir. Büyük bir matematik bilgini ve filozofudur. İsa’dan önce yaşayan yedi büyük bilginden en eskisi ve en ünlülerinden biridir. Hayatı hakkında kesin ve derin bilgiler yoktur.
Bir daire içine üçgen çizilmesi problemini çözümlemiştir. Ters açıların eşitliğini doğruladığı söylenir. Üçgenlerin özellikleri ve Thales bağıntıları, Mısır’daki piramitlerin yüksekliğinin bulunmasında kullanılmıştır.
Eski Yunan matematiği, öğretim yöntemlerine pek bağlı değildi. Belli okulları da yoktu. Thales, Pisagor ve Öklit, bu öğretim yöntemini ve kurallarını Yunan matematiğine getirmişlerdir.
Samos’lu Pisagor’un, İsa’dan önce 596 yıllarında doğduğu tahmin ediliyor. Doğumu gibi ölüm tarihi de kesin değildir. Hayatı hakkında çok az bilgiler vardır. Bu bilgilerin birçoğu da kulaktan kulağa söylentiler biçiminde gelmiştir. Yunan filozofu ve matematikçisidir. Ülkesinde hüküm süren politik baskılardan kaçarak, İtalya’nın güneyindeki Kroton şehrine gelmiş ve ünlü okulunu burada açarak şöhrete kavuşmuştur.
Söylentilere göre, Pisagor’un matematik, fizik, astronomi, felsefe ve müzikte getirmek istediği yenilik, buluşlar ve ışıkları hazmedemeyen bir takım siyaset ve din yobazları halkı Pisagor’a karşı ayaklandırarak okulunu ateşe vermişler, Pisagor ve öğrencileri bu okulun içinde alevler arasında İ.Ö.500 yıllarında ölmüşlerdir. Pisagor’un ve öğrencilerinin yaptıklarının birçoğu bu alevler arasında yok olup gitmiştir.
Geometride, aksiyomlar ve postülatlar her şeyden önce gelmelidir. Sonuçlar bu aksiyom ve postülatlardan yararlanılarak elde edilmelidir düşüncesini ilk bulan ve ilk uygulayan matematikçi Pisagor’dur. Matematiğe aksiyomatik düşünceyi ve ispat fikrini getiren yine Pisagor’dur. Çarpma cetvelinin bulunuşu ve geometriye uygulanması, yine Pisagor tarafından yapılmıştır. Yaşayış ve inanışı, ilimle açıklama ve yorumlamayı o getirmiştir. Gerçel eksenin sayı sisteminde kullanılmasını düşünmüştür.
Pisagor’un adını 2.600 yıldır andıran, onu ünlü yapan ve insanlığın varolduğu sürece de sonsuza kadar da andıracak meşhur teoremi şudur: Bir dik üçgende, dik kenarlar üzerine kurulan karelerin alanlarının toplamı, hipotenüs üzerine kurulan karenin alanına eşittir. Pisagor teoremi, rasyonel sayılarla ölçülemeyen uzunluğun da varolduğunu gösterir.
“Evrenin hakimi sayıdır. Sayılar evreni yönetiyor.” Sözleri de Pisagor’a aittir.
Pisagor’un mistik tarafları çoktur. Evren hakkında bugünkü gerçeklere uymayan düşünceler de ileri sürmüştür. Bunları bir tarafa bırakırsak, yine yaşadığı çağa göre matematikçi yönü çok ağır basar. Pisagor, Mısır’da ve Babil’de çok gezdi. Rahiplerden ilim öğrendi. Yaşadığı çağ ve aldığı rahip eğitimini göz önüne alınırsa, bunda yadırganacak pek bir şey yoktur. Matematiğe ispat fikrini getiren Pisagor için, sosyal ve şahsi yaşantısı bu kadar eleştiriye değmez.
Pisagor’dan önce, geometride, şekillerin aralarındaki bağlılıklar gösterilmeksizin elde edilenler, görenek ve tecrübeye dayanan bir takım kurallardı. Bu nedenle, daha önce gelen bir yetkili ne demişse o sürüp gidiyordu. Pisagor’un matematiğe ispat fikrini sokması bu yüzden çok önemlidir.
Elea’lıdır. Zeno deyince, paradokslar akla gelir. Zeno’nun kendi kendini yetiştirmiş bir köylü çocuğu olduğu söylenir.
Zeno’ nun paradoksları:
4. Bir zamanın yarısı, aynı zamanın iki katına eşittir.
Zeno, hıyanet veya ona yakın bir suç ile başı kesilerek öldürülmüştür. Diogenes Laertos’a göre, Zeno doğduğu şehrin tiranı tarafından işkence ile öldürüldü.
Zeno, varlığın birliğini kabul ettirmek için, haklı olarak ün yapmış kanıtlarıyla, hareketin olanaksızlığını göstermeye çalıştı. Zeno’nun paradoksları üzerine her çağın en büyük bilginleri kafa yormuşlardır. Olmayan ergi yöntemi çok erken bir tarihte bu paradokslara parlak bir biçimde uygulanmıştır.
Başlıca eserleri, ”Tabiat Üstüne” , ”Karşı Fikirler” ve Emperdokles üstüne eleştirili bir “Yorumlama” dır.
Abdera’lı Demokritus, Trakya’da bir İyonya kentinin bir kolonisinde doğmuştur. Babası çok zengindi. Gezginci bir bilgin olan Demokritus’un yüz yaşından fazla yaşadığı sanılmaktadır. O zamanda, matematik, biyoloji, coğrafya, astronomi, gökbilimi, ekonomi ve sosyoloji gibi çok değişik sahalara yönelik bir bilgisi vardı.
İlk atom kuramını ortaya atmıştır. Hiç bir şey yoktan var edilemez ve var olan hiçbir şey de tümüyle yok edilemez. Var olan her şey atomlar ve bu atomların arasındaki boşluklardır. Yunan dehasının doğurduğu atomizm ve bu felsefe okulunun Leucippe’le beraber kurucusu sayılır.
Demokritus’un deli olduğunu düşünenlere, ünlü tıp bilgini Hippocrates, ”Hasta değil, pek büyük bir akıl ve deha” olduğunu söylemiştir. En küçük atomdan tutunuz da en büyük yıldıza kadar her şeyin harekette olduğunu ta o zamanlar söylerdi.
Eserlerinin birçoğu zamanımıza kadar ulaşamamıştır. “Sayılar”, ”Geometri”, ”İrrasyoneller” ve “Teğetler” belli başlı eserleridir.
Knidos’lu Eudoxus, birçok bilgin gibi, gençliğinde çok fakirlik çekmiş biridir. Eudoxus orantılar kuramıyla Yunan matematiğini zirveye ulaştırmıştır.
Eudoxus, genç yaşlarında Tarentum şehrinden Atina’ya gitmiş, orada en iyi ve birinci sınıf matematikçi, idareci ve asker olan Archytas’ın (İ.Ö. 428-347) yanında öğrenim görmüştür.
Eudoxus, Atina’da sevilmediğini anlayınca, burayı terkederek, bugünkü Kapıdağı Yarımadasında bulunan Sızık şehrine gelerek burada tıp öğrenimi yapmıştır. Matematik dışında iyi bir hukukçu ve bir de iyi bir doktordu. Ciddi astromi çalışmalarıyla da ünlüdür. İlme çok büyük katkılarda bulunmuştur. Zamanının birçoğunu söylevler vermek ve felsefe yaparak geçirmiştir. Çağdaşlarına göre, ilmi yönüyle ve ilmi düşünceleriyle, birkaç yüzyıl ileridedir. Galile ve Newton gibi, gözleme ve deneye dayanmayan fikir, düşünce ve görüşleri hoş görmemiş ve inanmamıştır.
Eudoxus alan, hacim ve bazı cisimlerin yüzölçümlerini bulmuş ve bunlar hakkında birçok teoremin ispatını vermiştir. Gezegenlerin görünen hareketlerini açıklamış ve bu hareketlerinin dairesel olduklarını söylemiştir. Güneş saatini bulan, bir yılın 365 gün 6 saat olduğunu ortaya koyan ilk bilim adamıdır.
Bugün matematikte kullandığımız ve adına Archimedes aksiyomu dediğimiz aksiyomu yine Eudoxus’a borçluyuz. Bu da onun ünlü orantılı doğrular kuramıdır. İki doğru parçası veya iki sayı verildiğinde, en küçüğünün her zaman en büyüğünü kapsayan bir tam katı vardır. Bu aksiyom, matematik tarihinde uzun yıllar matematik çağlarının konusu olmuştur.
Archimedes, babası astronom olan Fidiyas’ın oğludur. Vücut ve fikir olarak aristokrat olan soylu Archimedes, İ.Ö. 287 yılında Sicilya Adası’nda Siraküza şehrinde doğmuştur. Archimedes’in, Siraküza kıralı II.Hieron’un akrabası olduğu söylenir. Bu nedenle, Archimedes, parasal yönüyle bir sıkıntı karşısında kalmadan zamanını ilme vermek fırsatını rahatça bulmuştur. Archimedes’in ilmi zekasını çok erken ve zamanında fark eden astronom babası, kendi ilmi bilgisiyle ona yürüyeceği ilmi yolu zamanında belirtmiş ve onu çok erken yaşlarda yönlendirmiştir.
Archimedes’e dünyadan gelip geçmiş üç büyük matematikçiden biri gözüyle bakılır. Bunlar sırasıyla, Archimedes, Newton, Gauss’tur.
Archimedes, uygulamalı ilimlere karşı büyük ilgi duyardı. Kuramsal matematiğe yaptığı hizmetlerin yanında, uygulamalı mekanikteki yaptıkları az kalır. Archimedes, halk müzesine konulabilecek en önde ve en büyük matematikçidir. Tıpkı Newton ve Hamilton gibi, hesaplarına daldığı zaman yemeklerini bile unutur yemezdi. Elbiselerine karşı Newton kadar ihmalkar ve hatta onu bile geçerdi. Garip davranışlarıyla başka büyük bir matematikçi olan Weierstrass’a benzer. Kendi halinde, kimseyle görüşmeyen bir kenara çekilmiş kendi kendine düşünen bir yapıdaydı
Dairenin alanı, çemberin uzunluğu, kürenin yüzölçümü ve hacmini ilk kez yine Archimedes hesaplamıştır. Pi sayısının hesabı yine ona aittir. Alan ve hacim hesaplamalarında bulduğu yöntemler yüzyıllar boyu hep önde götürülmüştür. En karmaşık eğrilerle sınırlı alanları ve yüzeylerle sınırlı hacimlerin bulunma yöntemini o getirmiştir. Daire, küre, parabol parçası, heliksin ardışık iki yarıçapı ve iki halkası arasında kalan alan, küresel parçalar, dikdörtgenlerin, üçgenlerin, parabollerin, hiperbollerin ve elipslerin asal ekseni etrafında döndürülmesinden oluşan yüzeyleri ve hacimleri bulmada, bulduğu bu yöntemi uygulamıştır. Silindir, koni, paraboloid, hiperboloid ve özel haller yine bu yöntemle yüz ölçüm ve hacim olarak hesaplanmıştır.
Newton ve Leibnitz’den 2.000 yıl kadar önce yaşayan Archimedes integral hesabını bulmuş ve problemlerinin birinde onların bulduğu diferansiyel hesaba başvurmuştur. Bu “sonsuz küçükler hesabı” dır. Archimedes yayını bugünkü dille söylersek, bir eğriye üzerindeki bir noktadan çizilen teğetin eğimi, bu eğrinin bu noktadaki türevine eşittir.
Archimedes’in hayatı, tüm olanakları yerine getirilen bir matematikçinin hayatı kadar sakin ve düzenli geçmiştir. Hayatının en karışık zamanı ve acıklı olanı son günlerine rastlar. Bu da Roma’lılarla Kartaca’lılar arasında İ.Ö. 264-146 yılları arasında yapılan Pön savaşları dönemine rastlar.
Archimedes, yere çizdiği şekil üzerinde bir matematik problemini çözmeye uğraşıyordu. Bir söylentiye göre, Roma’lı asker şeklin üzerine yürümüş ve Archimedes‘i kızdırmıştır. Bunun üzerine Archimedes’in, ”Aman daireme dokunma, bozma” diyerek yeniden probleme daldığı söylenir. Yine bir söylentiye göre, Archimedes Roma Şefi Marcellus’un yanına gitmek üzere kendisini izlemesini emreden askere, problemi bitirmeden kalkmayacağını söylemiştir. Problemin çözümünün uzun sürmesine canı sıkılan ve kızan asker, şanlı kılıcını çekmiş ve yetmiş beş yaşındaki yaşlı ve silahsız koca geometriciyi İ.Ö. 212 yılında canice öldürmüştür. İşte, bu büyük deha böyle yok edilmiştir.
Archimedes’in öldürülmesi her ne şekilde olursa olsun, ilim ve insanlığın beklediği medeniyet adına bunda daha büyük bir vahşet ve canilik görülmemiştir.
Yunan matematikçisi. Gelmiş geçmiş matematikçiler içinde adı geometriyle en çok özdeşleştirilen kişidir. Öklid, geometri dünyasında kapladığı bu seçkin yerini kendisinin büyük matematikçi olmasından çok, başlangıcından kendi zamanına kadar bilineni “Öğeler” adını verdiği kitaplarda toplamasına borçludur. Öğeler, dilden dile çevrilmiş, yüzlerce kez kopya edilmiştir, matbaanın icadından sonra da binlerce kez gözden geçirilmiş ve yeniden basılmıştır. Öklid derlemesinin tutarlı bir bütün olmasını sağlamak için, kanıt gerektirmeyen apaçık gerçekler olarak beş aksiyom ortaya koyar.
Öklid’in beş aksiyomu şunlardır:
Öğeler on üç kitaptan oluşmaktadır. Öklid geometrisi 19.yüzyıla kadar rakipsiz kaldı. Öklid’in yaşamı hakkında hemen hemen hiçbir şey bilmiyoruz.
Zamanında çok bilinmeyen, fakat 1600 yıllarında değeri anlaşılan Yunan matematikçilerinden biri de Bergama’lı Apollonius’tur. Eski devirlerin en büyük matematikçilerinden biridir. İ.Ö. 267 veya 260 yıllarında, Pamfiye denilen Teke Sancağının Perga kentinde dünyaya gelmiştir.
Matematikçi Pappus, Apollonius’un, bencil, üne düşkün, kibirli ve gururlu birisi olduğunu yazmaktadır. Apollonius’un yaptığı çalışmalar ve buluşları onun bu zayıf taraflarını örtecek kadar kuvvetlidir. Çarpmaya ait birçok buluşu vardır. Koniklere ait buluşları onu şöhretin zirvesine çıkarmıştır.
Euclides geometrisini benimseyerek onu daha ileri düzeylere götürmüştür. Teorik ve sentetik geometrici olarak 19. yüzyıldaki Steiner’e kadar Apollonius’un bir eşine daha rastlanamaz. Konikler adı altında bugün bildiğimiz elips, çember, hiperbol ve parabol kesişimlerine ait problemlerin birçoğu Apollonius tarafından bulunmuştur. Doğrular, çemberler ve eğrilerin konikler üzerine araştırma yapmıştır. Yine, analitik geometri özelliklerinden hemen hemen tümünü Apollonius’a borçluyuz.
Dairesel tabanlı ve tepesinin her iki tarafından sonsuza kadar uzatılmış bir koni bir düzlemle kesilirse, düzlemle koni yüzeyinin kesişimi olan eğri, doğru, çember, hiperbol, elips veya parabol olacağını ilk kez Apollonius göstermiştir. Merminin yörünge denkleminin bir parabol olacağı yine Apollonius tarafından bulunmuştur.
Pergel ve cetvel yardımıyla üç çembere teğet çizme, Apollonius problemi olarak bilinir. Yine, sabit iki noktaya olan uzaklıkları oranı sabit olan noktaların geometrik yeri, bu sabit noktaları birleştiren doğru parçasını, verilen orana göre içten ve dıştan bölen noktalar arasındaki uzaklığı çap kabul eden bir çemberdir.
Hipparchus, Yunan’lı matematikçi ve astronomdur. İlk sistematik astronomi ve trigonometriyi bulan kimsedir. Ekinoks noktalarının değişimi olayını bulmuştur. Binden fazla yıldız için bir katalog yaparak, Güneş ve Ayın uzaklığını hesaplamıştır. Enlem ve boylam daireleriyle, Dünya’daki herhangi bir noktanın konumunu belirtme yöntemini bulmuştur.
Tam adı Muhammed Bin Musa el-Harezmi olan bu büyük bilim adamı, Horasan’da doğmuştur. Bugünkü cebir ve trigonometrinin kurucusu sayılır. Avrupa’lıların en çok yararlandığı bir matematikçidir.
Cebir üzerine çok sayıda eser verdi. Descartes’e kadar batı bilim dünyasında egemen olan Harezmi ve Harezmi cebiriydi. Bu nedenle Harezmi dünya çapında bir matematikçidir. En önemli eseri, ”Cebir ve Mukayese Hesabı” dır. Deneyler, enlem ve boylam kitapları vardır. Bir de gökyüzü atlası vardır. Hindistan matematiğini dünyaya tanıtan yine Harezmi’dir.
Gerbert, 945 yılında Auvergne’de bir kilisenin önünde rahipler tarafından bulunup, büyütülmüştür. Gerbert’in çok yetenekli ve parlak bir zekaya sahip olduğu kilisede hemen fark edilir. Gerbert bu kilisede tam yirmi yıl kalır.
Dokuz rakamla hesap yapan ilk batılı bilgin Gerbert’tir. Bu dokuz rakamı İspanya’nın sınır kentinde öğrenmişti. Gerbert bu dokuz rakamla oldukça kolay ve çabuk hesaplar yapıyordu. Bu nedenle kendisine sihirbaz ve büyücü gözüyle bakıyorlardı.
Burada ilginç olan yan, Gerbert’in sıfır rakamını bilmemesiydi. On rakamı ile hesap yapılması, Gerbert’ten tam yüzyıl sonra büyük Türk matematikçisi Harezmi’nin “Hesap Kitabı” nın Latinceye çevrilmesinden ve Orta İspanya’dan batıya ulaşması ile gerçekleşmesi olmuştur.
Asıl adı Gıyaseddin Ebu’l Feth Bin İbrahim El Hayyam’dır. 18 Mayıs 1048’de İran’ın Nişabur kentinde doğdu.
İlgilendiği ilimler; matematik, fizik, astronomi, şiir, tıp, müzik’tir. Daha yaşadığı dönemde İbn-i Sina’dan sonra Doğu’nun yetiştirdiği en büyük bilgin olarak kabul ediliyordu. O herkesten farklı olarak yaptığı çalışmalarının çoğunu kaleme almadı, oysa o ismini çokça duyduğumuz teoremlerin isimsiz kahramanıdır.
Eserleri arasında; Cebir ve Geometri Üzerine, Fizikler Bilimler Alanında Bir Özeti, Oluş ve Görüşler, Bilgelikler Ölçüsü, Akıllar Bahçesi yer alır. En büyük eseri Cebir Risalesi’dir.
Matematik bilgisi ve yeteneği zamanın çok ötesinde olan Ömer Hayyam denklemlerle ilgili başarılı çalışmalar yapmıştır. Bunun yanısıra, binom açılımını da bulmuştur. 4 Aralık 1131’de doğduğu yerde öldü.
Piza’lı Leonardo Fibonacci, Rönasanstan önce, Asya ülkelerinin matematiğini Avrupa’ya en etkili olarak taşıyan ve götüren biri olarak bilinir. Yaşam öyküsü hakkında hemen hemen hiçbir şey bilinmiyor. Yalnız, babası karşı sahillerdeki müslümanlarla ticaret yapan bir tüccardı. Babası, Leonardo’ya hesap öğretmesi için Arap bir hoca tuttu.
Öğretmenlerin ona verdiği matematik dersleri daha çok yaşam koşullarıyla ilgiliydi. Matematiği iyice kavradıktan sonra, sayılar kuramı ve geometri üzerine iki kitap yazmıştır. Buluşlarının en ünlüsü, Fibonacci dizisidir. Doğadaki çiçeklerin yaprakları üzerinde bile araştırma yapıyor, onların düzenini ve doğadaki olayların sayılarla ifade edilebileceğini keşfetmeye çalışıyordu. Bunlara daha sonra ”altın oranlar” denmiştir.
Leonardo Fibonacci’nin en büyük hizmeti, Harezmi’nin matematiği ile, çok kullanışlı olan Hint ve Arap karışımı sayılarını batıya tanıtmakla çok büyük bir görev yapmıştır.
John Napier, Merchiston-Edinburg’da 1550 yılında doğdu. Merchiston Baronu ve İskoçya’lı bir matematikçi olan Napier, logaritmanın bulucusu olarak bilinir. Zaten aritmetik için üç aşama vardır. İlki, sayıların on tabanına göre yazılması, ikincisi logaritmanın bulunuşu ve üçüncüsü de şimdiki bilgisayarlardır.
Napier, Saint Andrews Üniversitesi’nde eğitim görmüş ve matematiği de içinden gelen bir merak olarak izlemiştir. Kendisi amatör bir matematikçidir. Sayısal hesaplamaları kolaylaştıracak bir yol ararken, önce Napier cetvelleri diye bilinen, üzerinde rakamlar yazılmış küçük değnekler yardımıyla yapılan bir çarpma veya bölme yöntemi buldu. 1,2,3,... şeklindeki aritmetik dizi ile, buna karşılık gelen 10,100,1000,... biçimindeki geometrik dizi arasındaki ilişkiyi gördü. 1614 yılında yazdığı “Logaritma Kurallarının Tanımı” adlı eserinde, aritmetik dizi ile geometrik dizinin karşılaştırılmasından, matematiğe logaritma kavramını getirdi. Buradaki aritmetik dizi, geometrik dizinin logaritmasıdır.
Napier, 1618 ve 1624 yılları arasında kusursuz iki logaritma cetveli yayınladı. Bu eser onun tam yirmi yıllık çalışmasının ürünüdür. Napier’in bu konuda çok sayıda eseri vardır. Bazı hesap makinalarının temellerini veren iki kitabı, 1617 yılında yayınlandı. 1617’de Edinburgh’ta öldü.
Johannes Kepler, 1571 yılında Württemberg’de Wiel’de doğdu. Tanınmış bir Alman astronom ve modern astronomiyi kuranlardandır.
Gelişmiş merceklerin teleskopta kullanılmasına önderlik ederek ışık bilimine de yardım etti. Gezegenlerin Güneş etrafındaki hareketlerini kesin olarak hesaplayan Alman gökbilimcisidir. Güneşin, gezegenlerin merkezi olduğunu benimsedi. Gezegenlerin yörüngelerinin, odak noktalarının birinde Güneş olan elipsler olduğunu saptadı. Bu Kepler yasalarının ilkidir. Üç tane buluşuna “Kepler Yasaları” denir. Bunlar:
Kepler’in bu yasalarının matematiksel olarak gösterilmesi de oldukça zordur. Kepler ayrıca, enlem ve çizgilerini ilk kez kesin olarak hesaplayanlardan biridir. 1630’da öldü.
Yalnız sükun ve rahat istiyorum diyen Rene Descartes, Avrupa’nın savaşa sürüklendiği yıllarda, Fıransa’nın Tours kenti yakınında La Haye’de 31 Mart 1596’de doğdu. Asılzade, asker ve matematikçi olan Descartes, metafizik ve kuramsal fikirlerden çok, analitik geometrisi ile yeni bir çığır açmıştır. Savaşlar, kıtlıklar, salgın hastalıklar, fakirlik, pislik ve cahilliğin hüküm sürdüğü bir ortamda yaşıyordu.
Descartes, asil bir aileden geliyordu. Babası varlıklıydı. Rene’nin doğumundan birkaç gün sonra annesi öldü. Babasının küçük filozofu Descartes, çevresinde ve dünyada gördüğü her şeyin nedenini soruyordu. Descartes’in yetenekleri daha okul sıralarında ortaya çıkmıştı. 14 yaşındayken, okuldaki eğitimin insani bakımdan kısır olduğunu sezmişti. Körü körüne inanılması ve bağlanılması gerekenleri temelsiz görüyor ve ispatsız hiçbir şeyi kabul etmiyordu. Bu yüzden de papazlarla tartışmaya ispat yoluyla başladı. Her şeyden şüphe ediyordu.
Her girdiği işte canla başla çalışıyordu. İki yıl matematik araştırmalarını yaptığı evi, saygısız arkadaşları yine buldu. Çekilmeyen arkadaşlarından kurtulup huzura ve sükuna kavuşmak için savaşa gitmeye karar verdi. Fakat, burada da istediği sükunu bulamadı. Almanya’ya gitti. Bayram, tören ve şölenlere merak sardı. Yeniden askerliğe döndü.
Avrupa’daki iskolastik düşüncenin egemenliğini sürdürdüğü ve karanlık çağın sona erdiği yıllarda, Descartes’i dinsizlikle de suçlamışlardır. Onun dini fikir ve düşünceleri rasyonelistti ve oldukça sadeydi. Sağlıksız ve cılız büyüdüğü için, yıllarca ölüm korkusu içinde yaşamıştır. Paris’te sükunetli tam üç yıl geçirmiştir.
Onun daha çok soyut olan matematik bir kafası vardı. Uzun yıllar Hollanda’da kaldı. Optik, fizik, anatomi, embriyoloji, tıp, astronomi, meteoroloji ve gökkuşağı üzerindeki incelemelerini sonuçlandırmıştı. Her olaya bir hammadde gözüyle bakıyor ve ondan yeni bir şeyler çıkarmayı düşünüyordu. Bu nedenle çok yenilikçiydi. Yenilik onun yaşamı ve ruhuydu.
Biraz sükuna kavuştuğunu sandığı elli yaşları yöresinde, karşısına İsveç Kıraliçesi Christine çıktı. Bilmesi gereken her şeyi bilen, hatta daha fazlasını öğrenmiş olan ve çok yönlü olan on dokuz yaşındaki Christine, Descartes’i kendisine özel öğretmen olarak tuttu. Christine’nin insafsız ve bitmek tükenmek bilmeyen çalışmaları onu yedi bitirdi. Kış, soğuk ve Christine’nin amansız çalışmaları sonunda hastalandı. Doktorları kabul etmedi. 11 şubat 1650’de öldü.
Descartes, yeni bir geometriyi kurmuş ve modern geometrinin doğmasına olanaklar vermiştir.
İtalyan papazı ve matematikçisi olan Bonaventura Cavalieri, Milano’da doğdu. Galile’nin en iyi öğrencilerinden biri olan Cavalieri, 1629 yılından ölünceye kadar Bologna’ da matematik okuttu. Astronomi ve küresel trigonometriyle ilgilendi. Logaritma ve hesaplarının İtalya’da uygulanmasında öncülük etti. ”Süreklilerin Bölünmezleri Yolundan, Yeni Bir Yöntemle İlerletilmiş Geometri” kuramıyla büyük ün kazanmıştır. Bu kuram, geometrik büyüklükleri, sonsuz öğeli bir sayıdan oluşmuş kabul eder. Bu öğeler, geometrik büyüklüğün ayrılabileceği en son terimdir. Bu nedenle de bölünemez olarak nitelenir. Uzunlukların, yüzeylerin ve hacimlerin ölçülmesi sonsuz sayıda bölünmezlerin toplamından başka bir şey değildir. Belirli bir integralin hesaplanması da bu ilkeye dayanır. Cavalieri, bu teoremiyle bugünkü sonsuz küçükler hesabı denen analizin öncüsü olarak sayılabilir. 1647’de Bologna’da ölen Cavalieri’nin kendi adıyla anılan postülatları, teoremleri ve bunlardan başka kitapları da vardır.
Fermat’ın babası bir deri tüccarı ve annesi de bir hukukçunun kızıydı. Fransa’da Lomagne’de doğdu. Oldukça sessiz ve sakin bir yaşam sürdürmüştür. Olgunluk çağındaki başarıları ve eserleri onun parlak bir öğrenci olduğunu gösterir.
Fermat’ın hayatının tarihi matematiktir. Birçok yabancı dil de öğrenmiştir. Memurluğunun yoğun işlerinden geriye kalan zamanlarında matematikle uğraşmıştır. Archimedes’in eğildiği diferensiyel hesaba geometrik görünümle yaklaşmıştır.
Eğrilerin çiziminde maksimum ve minimum noktalarının önemi bilinmektedir. İşte bu kavramları koyan yine Fermat’tır. Oldukça kolay gibi görülen bu problemin matematikte ve fizikte çok geniş ve ileri uygulamaları vardır. Ayrıca, bu kavramları ışık bilmine uygulamasını çok iyi beceren yine odur. Buna bağlı olarak yansıma, kırılma, geliş ve yansıma açıları üzerine yaptığı bağlılıklar önemini bugün bile korumaktadır. Fermat, analitik geometriyi üç boyutlu uzaya aktarmıştır. Amatör bir matematikçi ve düzenli bir evrak memuru olan Fermat’ın en önemli matematik çalışması sayılar kuramı üzerinedir. Asal sayılar üzerinde çok durmuştur.
n-kenarlı düzgün bir çokgenin n-kenarı ve n-açısı eşittir. Eski Yunanlılar pergel ve cetvelle 3, 4, 5, 6, 7 ve 10 kenarlı düzgün çokgenleri çizebiliyorlardı. İ.Ö. 400 yıllarında, pergel ve cetvelle 7, 8, 11, 13,... kenarlı çokgenlerin çiziminin yollarını bulamamışlardı. Fermat bu problemi çözdü.
Fermat, eserlerini ve buluşlarını genellikle yayınlamaz ve birçok teoremlerini de karalamalar şeklinde bırakırdı. Hatta, bazı teoremlerin sadece ifadelerini yazdığı görülmüştür. Yani, ispata bile gereksinim duymamıştır. Basit gibi görünen bir problemini Euler, tam yedi yılda ancak ispatlayabilmiştir. Ölürken çalışmalarının birçoğunu da yaktığından, bize bilgi kalmamıştır. Fermat’ın bu davranışı matematik dünyası için bağışlanamaz.
Fermat, hiçbir zaman gerek Descartes ve gerekse Pascal gibi hayali ve çekici olan felsefelere kendini kaptırmamıştır. Kuramsal matematiği en yüksek düzeye çıkarmıştır.
12 Ocak 1665’te hayatında hikaye edilecek hiçbir şey bırakmadan ölmüştür. Fermat bu buluşlarını saklamayıp yayınlasaydı, matematikte daha birçok yenilikler birbirini izleyecekti. Ne yazık ki, Fermat bizi bundan yoksun bırakmıştır.
Pascal, 19 Haziran 1623 günü Fransa’da Clermont’ ta doğdu. Babası kültürlü bir adamdı.
Descartes ve Fermat gibi büyük matematikçilerle çağdaş olması bir yerde kendisi için bir şanssızlıktı. Bu nedenle, tek başına oluşturabileceği olasılıklar kuramının keşfini Fermat ile paylaştı. Kendisini “ harika çocuk” diye ünlü yapan yaratıcı geometri fikrini, kendisinden daha az ünlü olan Desargues’dan esinlendi. Daha çok din ve felsefe konularına eğildiği için matematiğe az zaman ayırdı.
Pascal, çok erken gelişen bir çocuktu. Fakat, vücutça oldukça zayıftı. Bunların tersine kafası çok parlaktı. Çok küçük yaşta olmasına rağmen, matematiğe gösterdiği ilgi çok dikkat çekiyordu. Hatta matematik problemleriyle gece gündüz uğraşmaya başladı. Sağlığının bozulacağından kuşkulanan babası, bir aralık onun matematik çalışmasına engel olduysa da onun bu davranışı Pascal’ı matematiğe daha çok yöneltti.
Hiçbir yardım görmeden ve hiçbir geometri okumadan, çok küçük yaşta bir üçgenin iç açılarının toplamının 180 derece olduğunu kanıtlamıştır. Daha önce hiçbir kitabı okumadan, Euclides’in birçok önermesini ispatlamıştı. Pascal kendi kendine bir geometrici olmuştu.
Pascal, on altı yaşından önce, 1639 yılında, geometrinin en güzel teoremini ispat etti. İngiliz matematikçisi ünlü Sylvester, Pascal’ın bu büyük teoremine “Kedi Beşiği” adını vermiştir. Pascal, on bir yaşına gelince sesler hakkında bir eser vermiştir. On altı yaşındayken, konikler üzerine bir eser yazarak, ünlü Descartes’i hayretlere düşürmüştür. On sekiz yaşına gelince, şimdi Paris sanayi müzesinde saklanan hesap makinesini bulmuştur. Fizikte, havanın ağırlığını, sıvıların denge halini ve basıncı hakkında Pascal kanunlarını bulmuştur.
Pascal, on yedi yaşından ölümü olan otuz dokuz yaşına kadar ızdırapsız ve acısız gün görmedi. Hazımsızlık, mide ağrıları, uykusuzluk, yarı uyuklamalar ve bu ağrıların verdiği gece kabusları onu yedi bitirdi. Böyle olmasına rağmen, yine de bu ağrılar içinde durmadan çalışıyordu.
Yirmi üç yaşlarında, geçici bir felç geçirdi. Bu ona çok ağrılar verdi. Her şeye rağmen, düşüncesi ve kafasının çalışmaları sürüyordu.
1648 yılında Toriçelli’nin çalışmalarını inceleyerek, onun da önüne geçti. Yükseklikle basıncın değiştiğini saptadı.
Pascal, kız kardeşinin de etkisi ile 1654 yılından sonra kendini dünya işlerinden ve matematikten çekerek, hıristiyanlığın o koyu tutuculuğu içine gömülüp gittiği ve taassubun kurbanı olduğu bilinen bir gerçektir.
1658 yılının bir gecesinde, uykusuzluk ve diş ağrılarından kıvranan Pascal, kerpetenin egemen olduğu bir zamanda, korkunç ağrılarını unutmak amacıyla, birçok ünlü matematikçinin uğraştığı zarif sikloid eğrisine daldı. Tüm ağrılarının geçtiğini gördü. Ya da, sikloid üzerine o kadar daldı ki, tüm ağrı ve acılarını unuttu. Tam sekiz gün sikloid geometrisi üzerine çalıştı.
1658 yılında kendini oldukça hasta hissetti. Kısa aralıklarla gelen uyuklamalar dışında, şiddetli ve dinmek bilmeyen baş ağrıları ona çok eziyet ediyordu. Tam dört yıl bu ağrılarla kıvrandı. 1662 yılının Haziran ayında otuz dokuz yaşındayken öldü. Ölümünden sonra yapılan otopsisinde, ağrılarının nedeninin ciddi bir beyin hastalığından ileri geldiği saptandı.
Pascal, Fermat ile birlikte olasılıklar kuramını kurmakla, yeni bir matematik dünyası yaratmış oluyordu. Pascal üçgeni, binom açılımındaki katsayıları bulmaya yarar.
Hıristiyan dini, mezhepler ve sonu gelmez ağrılar içinde bir dahi, maddi olarak yok olup gitmiştir. Fakat, bıraktıklarıyla yaşamaktadır.
Hollandalı fizikçi, matematikçi ve astronom olan Christiaan Huygens, 1629 yılında La Haye’de doğdu. Constantin Huygens’in oğlu olan Christiaan, bilimsel bir ortamda yetişti. Leiden ve Breda Üniversiteleri’nde okudu. Geometri ile ilgili eserlerini bastırdıktan sonra fiziğe yöneldi. Kendi adıyla anılan saati buldu.
Huygens’in yalnız matematik alanındaki çalışmaları bile onu ünlü yapmaya yeter. 1656’da, olasılıklar kuramının ilk eksiksiz incelemesini yaptı. Açan ve açılan eğriler kuramını kurdu. Bu kuramla, eğrilik merkezinin tanımını yaptı. Sikloidin özelliklerini buldu. Şisoit’un doğrulaştırılmasını başardı. Logaritma kuramını Huygens kurdu. Zincir eğrisi problemini çözümledi. Kepler’in pozitif göz merceklerinden daha üstün olan negatif göz merceklerini buldu. Huygens’in en büyük buluşları fizikte, özellikle mekanik ve optik alandadır. Yansıma ve kırılma kanunlarını buldu. Kuramsal ve uygulamalı bir adamdı. 1695’de doğduğu yerde ölmeden önce, Newton’un futon kuramına karşı çıktı.
İskoçya’lı matematikçi ve fizikçi olan James Gregory, 1638 yılında Aberdeen’da doğdu. 1663’te kendi adını taşıyan ve “Optica Promota” adlı eserinde anlattığı yansımalı teleskopu buldu. Edinburg Üniversitesi’nde matematik profesörü oldu. Arı geometri ve analitik geometri ile ilgilendi. Pi sayısının değerini yeniden hesapladı. Yay ve teğet serisi açılımlarını buldu.
Çok kısa süren yaşam süresinde çok sayıda sonuçlar buldu. Özellikle diferansiyel ve integral hesap üzerinde çalışmaları vardır. Sonsuz küçük hesabında da çalıştı. 1675’te öldüğünde çok gençti.
“Herkesin beni nasıl gördüğünü bilmem. Ben kendimi, deniz kenarında oynarken, önünde hiç keşfedilmemiş engin gerçek okyanusu yayılmış duran ve cilalı bir çakıl taşı ya da güzelce bir istridye kabuğu bulmakla zevk duyan bir çocuk gibi görüyorum.” Newton.
İşte, uzun yaşamının son yıllarında kendisi hakkında böyle hüküm veren İsaac Newton, 1642’de Woolsthrope kasabasının bir şatosunda yaşayan bir çiftçi ailesinin oğlu olarak dünyaya geldi. İngiliz ırkının en büyük zekalı adamı olarak nitelenen Newton’un babası, oğlunun doğumundan önce otuz yaşında öldü. Annesinin söylediğine göre, zamanından erken doğan küçük Newton, o kadar ufak tefekti ki bir litrelik kavanozun içine bile sığabilirdi. Newton’un çocukluğu da dinç, canlı ve kuvvetli değildi. Diğer arkadaşları gibi eğlenceli vakit geçirme yerine, eğlencelerini ve oyunlarını kendi yaratıyor ve bunlarda parlak zekası ortaya çıkıyordu. Geceleri köylüleri korkutmak için kandilli uçurtmaları, tümü ile kendisinin yaptığı ve oldukça güzel işleyen hareketli oyuncaklar, su çarkları, gerçekten buğday öğüten bir değirmen, küçük kız arkadaşları için iş kutuları ve oyuncaklar, resimler, güneş saatleri, tahtadan yapılmış ve gerçekten işleyen duvar saati gibi şeyler onun çok erken yaşlarda yaptığı buluşlardı.
Newton, daha on sekiz yaşında, Cambridge’de öğrenci olduğu yıldan başlayarak, evrensel bir beğeniyle karşılandı. Üniversiteyi bitireli iki yıl olmadan, bilim dünyasınca alkışlanıyor ve hükümdarlardan saygı görüyordu.
Newton, ürkek yapılı, sinirli, çabuk kızan ve itirazla karşılanmaktan korkan bir yapıya sahipti. Eserlerini ancak kendisini seven dostlarının zoruyla bastırmıştır. Eserlerinin eleştirilmesinden kaçardı. ”Optiks” adlı eserinin eleştirilerine dayanamamış ve bu eseri yazdığına pişman olmuştur. Newton, Galile’nin uğraşmak zorunda kaldığı sürtüşmelerle karşılaşmış olsaydı, bir satır bile yayın yapamazdı. Yerçekimi genel kanununu 1687 yılına kadar yayınlamadı. Tam yirmi yıl bu genel çekim kanunu kuramını geliştirdi.
Grantham okuluna devam ettiği sıralarda ve Cambridge’e hazırlanırken köyün eczacısı Mr. Clarke’ın evinde kalıyordu. Orada eski bir kitap koleksiyonu buldu ve onları yutarcasına okudu. Newton hayatında hiç evlenmedi.
Newton’un hareket kanunları:
Newton’un en önemli buluşlarından birisi de evrensel çekim kanunudur. Newton bir gün elma ağacının gölgesinde otururken başına bir elma düşer. Bunun üzerine uzun uzun düşünür. Yine uzun çalışmalardan sonra ünlü, kütlelerin birbirlerini çekim kanununu bulur. Newton’a, bu buluşlarını nasıl bulduğu sorulduğunda, sürekli düşünmeyle, diye yanıt vermiştir.
Newton’un en önemli buluşu, diferansiyel ve integral hesabı keşfetmesidir. Zaten Newton’u dünyada gelmiş geçmiş üç büyük matematikçiden biri yapan buluşu budur.
Newton, 1661 yılının Haziran ayında Cambridge’deki Trinity College’e girdi. Newton’un matematik öğretmeni İsaac Barrow hem ilahiyatçı ve hem de matematikçiydi. Matematikte parlak fikirli olan Barrow, öğrencisinin kendisinden çok ileride olduğunu kabul ediyor ve 1669’da matematik kürsüsünü bırakıp sırası gelince yerini o eşsiz büyük deha Newton’a bırakıyordu.
1664 ile 1666 yılları arasında, yirmi bir yaşından yirmi üç yaşına kadar çok yoğun bir çalışmaya girmiş ve yaptığı çalışmaları uzun zaman gizli tutmuştur. Ocak 1664 yılında üniversiteyi bitirmiş ve lisans diplomasını almıştır.
Bir kuyruklu yıldız ile Ayın etrafındaki, Ayla ilgili şeyleri incelerken hastalandı. Bulduğu sonuçları da gizli tutmuştu. Bu iki yıl içinde diferansiyel ve integral hesabı keşfetmiş, genel çekim kanununu bulmuş ve beyaz ışığın analizini deneysel olarak yapmıştı. Bunların tümü, yirmi beş yaşından önce bulunmuş şeylerdi. 20 Mayıs 1665 tarihli bir yazısıyla, bir eğrinin üzerindeki bir noktadaki teğeti ve eğriliğini verecek yöntemini daha yirmi üç yaşındayken yayınlıyordu. İşte bu, diferansiyelin bulunuşunu müjdeliyordu. Bu sıralarda ünlü sonsuz küçükler hesabına doğru yaklaşıyordu. Yine bu sıralarda, binom formülünü buluyordu.
Evrensel genel çekim kanununun yayınlanmasının yirmi yıl gecikmesinin nedeni, kendisine yanlış sonuçların verilmesinden doğmuştur. Doğru hesabı yapabilmek için bir integralin hesap edilmesi gerekiyordu. Bugün bu integral kolaylıkla çözülebilir. Fakat Newton’u tam yirmi yıl düşündürmüştür. Çünkü, integral hesap yöntemleri bugünkü kadar geliştirilmemişti.
1667 yılında Cambridge’e dönüşünde Trinity Collegei’ne üye olarak atanan Newton artık rakipsizdi. 1668’de tek başına yansımalı teleskopu yapmış ve uyduları incelemekte kullanmıştır. ”Philosophy Naturalis Principia Mathematica” adlı eserini yazmaya başladığında geceli gündüzlü çalıştı. Ünlü pertürbasyon kuramını ortaya atmıştır. Bu kuram daha sonra ilerletilerek elektronların yörüngelerine uygulanmış, on dokuzuncu yüzyılda bu kuramla Neptün ve yirminci yüzyılda da Plüton gezegeni keşfedilmiştir.
Principia’ları yazmak için on sekiz ay uykusuz ve gıdasız kalan Newton, ellili yaşlarına yaklaşıyordu. Bu yorgunluktan sonra 1692 sonbaharında iyice hastalandı. Yiyeceklere karşı olan tiksinti ve sürekli uykusuzluk neredeyse onu çıldırtıyordu. Ağır hasta olduğu tüm Avrupa’ya yayıldı. Düşmanları bile, daha sonra iyileşmesine çok sevindiler.
Newton, 1696’da elli dört yaşında darphanede para basımı düzenlemekle görevlendirildi. 1701 ile 1702 yıllarında, Cambridge Üniversitesi’ni parlementoda temsil etti. 1703 yılında Royal Society’nin başkanlığına seçildi. Ölünceye kadar da bu makamda kaldı. 1705 yılında Kıraliçe Anne tarafından chevalier’lik rütbesi ile onurlandırıldı.
1696 yılında Bernoulli ve Leibnitz, Avrupa’lı matematikçilere iki soru ile meydan okuyorlardı. Altı ay uğraşıldıktan sonra yeniden ortaya atılan problemleri, Newton ilk kez 29 Ocak 1696 günü akşamı darphaneden yorgun argın evine döndüğünde bir arkadaşından duydu. O gece her iki problemi de çözdü. Ertesi gün isim vermeden her iki çözümü de Royal Society’ye gönderdi. Çözümleri gören Bernoulli, hemen oradakilere, ”Ha! Arslanı pençesinden tanıdım” diye haykırdı.
Newton 1716 yılında yetmiş yaşındayken bile fikri yapısı oldukça dinçti. Bu sırada Leibnitz yine ortaya attığı bir problemle Avrupa matematikçilerine meydan okuyordu. Newton problemi darphaneden akşam eve dönüşünde saat beşte almıştı. Çok yorgun olmasına karşın, problemin çözümünü o akşam hemen buldu. Tüm matematik tarihi boyunca, karşısına çıkan güçlükleri zekasını kullanarak yenen ve bu güçlükleri çözen Newton gibi biri gelmemiştir. O, İngiliz ırkının gelmiş geçmiş en büyük zekasıydı. Yaşadığı uzun yılları en mesut biçimde geçiren ve yaptıklarının sonuçlarını gören, takdir edilen, şan ve şöhretle alkışlanan tek matematikçi Newton’dur. Ömrünün son üç yılını çok ağrı ve acılar içinde yakalandığı böbrek taşı hastalığından çekti. Ölümüne yaklaşırken bir de öksürüğe yakalandı. Birkaç gün içinde ızdırap ve acıları duymayan bir rahatlığa erişti. 20 Mart 1727 sabahı bir ile iki arasında bu dev söndü. Cismen ölen, İngiliz ırkının en büyük dehasına karşın, elma yine yere düşmektedir.
“Bende o kadar fikir var ki, eğer benden daha iyi görmesini bilenler bir gün onları derinleştirecek ve benim zihin emeğime kendi kafalarının güzelliğini katacak olurlarsa, sonraları belki bir işe yarayabilir” diyen Gottfried Wilhelm Leibnitz, 1 Temmuz 1646 günü Leipzig’te doğdu. Babası ahlak ilmi öğretmeni olup, üç nesilden beri Saksonya hükümetine hizmet etmiş bir aileden geliyordu. Bu nedenle ilk yılları oldukça ağır bir politika ile yüklü bir bilgiçlik havası içinde geçti.
Leibnitz altı yaşındayken babasını kaybetti. Tarih hevesini babasından almıştı. Sekiz yaşında Latince’ye başladı. Kendi gayreti ile Yunan’ca öğrendi. ”Characteristica Universalis” adlı ilk denemesini verdi. Bu eser, metafiziğin anahtarıdır.
Leibnitz, on beş yaşındayken Leibzig Üniversitesi’ne bir hukuk öğrencisi olarak girdi. 1663 yılının yazını Jena Üniversitesi’nde geçirdi. Leibzig’e dönünce yeniden hukuka başladı. 1666 yılında yirmi yaşındayken doktora sınavı için hazırdı. Leibnitz’e gıpta eden titiz Leibzig Fakültesi ona resmen gençliğinden dolayı, gerçekte tüm profesörlerden fazla hukuk bildiği halde, doktora ünvanını vermeyi kabul etmedi. Halbuki, 1863 yılında on sekiz yaşındayken, parlak bir tezle başölye ünvanını almıştı. 5 Kasım 1666 yılında Alfdorf Üniversitesi’ne bağlı Nürnberg Üniversitesi “Tarihi Yöntem” adlı çalışmasından dolayı doktora ünvanını verdi.
Durmadan okurdu, yazardı ve düşünürdü. Matematik çalışmalarının çoğunu kendisini çağıran aristokratlara giderken, çağın o kötü yollarında, kötü arabalar içinde sallana sallana yazmıştır. Bu çalışmaların tümü bugün Hannover kütüphanesinde bağlı olarak durur.
1666 yılında olasılıklar kuramına başladı. Bu sıralarda öğrenciydi. Matematik Leibnitz’in parlak zekasının fışkırdığı bir sahadır. Bundan başka hukuk, din, siyaset, tarih, edebiyat, mantık, metafizik ve kuramsal felsefe konularında sayısız eser bırakmıştır. Bundan dolayı kendisine evrensel deha denmektedir. Verimsiz gibi görünen soyut olasılıklar kuramının öncüsü Leibnitz’dir.
Leibnitz, matematik ve mantık alanında çağının iki yüzyıl ilerisindeydi. Diferansiyelin geometrik bir yorumunu verdi. Bu matematiğe en büyük hizmetti. Bugün, Leibnitz’in olasılıklar yöntemi, gösterim mantığı ve gelişmelerinde meydana çıkarıldığı biçimde analiz için, analizin kendisi kadar önemlidir.
Gauss’un söylediği gibi, Leibnitz, matematik bilgisinin çoğunu boş yere israf etmiştir. Eğer, onun eğildiği her konuda verdiği eserleri toplayacak büyük adamlar olsaydı, bugünkü ilim ve özellikle matematik tarihi bambaşka olurdu. Bunun yerine, yirmi yaşında Mainz Elektörü için bir hukuk danışmanı ve hatırı sayılır bir ticaret memuru oldu.
1675 yılında Royal Society’nin ilk yabancı üyesi oldu. Yine aynı yıl, diferansiyel hesabın bazı basit formüllerini çıkarmış, kendi sözüne göre, temel teoremi keşfetmişti. 1677 ile 1704 yılları arasında, Leibnitz’in yaptığı çalışmalar tüm Avrupa’ya yayıldı.
Leibnitz’in uğraştığı konuların tam bir listesini vermek olanaksızdır. Onun en az başarılı olduğu saha mekanik ve fizikti. En önemli eserleri içinde birçok akademiyi kurması ve onları çalıştırması sayılabilir.
Altmış sekiz yaşına doğru iyice çöktü. Eski zekası kalmadı. Hastaydı. Çok çabuk ihtiyarlıyordu. Leibnitz, yetmiş yaşına gelince Hannover’de öldü.
Jacques Bernoulli Daniel Bernoulli Jean Bernolli
“Bu adamlar şüphesiz birçok şeyler başarmışlardır ve seçtikleri hedefe en iyi bir biçimde varmışlardır" diyen Jean Bernoulli, Bernoulli ailesinin neler yaptıklarını belirtmek istemektedir.
Üstün zekalı soylarının geçmişleri uzun uzun genetikçiler tarafından incelenmiştir. Üç veya dört nesilde sekiz on tane üstün zekalı matematikçi veren Bernoulli ailesi incelemeye değer. İçlerinden birçoğu hukukta, bilginlikte, edebiyatta, serbest mesleklerde, idari alanlarda ve görevlerde ve sanatta gerçek bir üstünlük göstermişlerdir. Matematik alanında daha çok Bernoulli soyunun ikinci ve üçüncü kuşakta sivrildiğini görmekteyiz.
Bernoulli ailesi, diferansiyel ve integral hesabın gelişmesinde, uygulanmaya konulmasında ve tüm Avrupa’ya yayılmasında en önde yer almışlardır.
Bernoulli’ler, Saint-Barthelemy toplu öldürmelerinde olduğu gibi, hügnoların katolikler tarafından toplu öldürülmelerinden kurtulmak için 1583 yılında Anvers’ten kaçan bir ailenin soyudur.
Şimdi, bu aileden gelen sekiz matematikçinin önemli ilmi çalışmalarını sırasıyla kısaca verelim.
I. Jacques, Leibnitz tarafından ortaya atılan diferansiyel ve integral hesabın şeklini inceledi. 1687 yılından, ölümü olan 1705 yılına kadar Bale’de matematik profesörlüğü yaptı. Analitik geometri, olasılıklar kuramı ve değişimler hesabına ait buluşları çok değerlidir. Sikloidin en çabuk iniş eğrisi olduğu, I. Jacques ve I. Jean kardeşler tarafından 1697 yılında, başka bilginlerle hemen hemen aynı zamanda bulundu. I. Jacques’in ölümünden sonra 1713 yılında olasılıklar kuramında “Ars Conjectandi” adlı büyük eseri yayınlandı.
I. Nicolas ta kardeşleri gibi matematikçi yaratılmıştı. On altı yaşında Bale Üniversitesi’nden felsefe doktoru ünvanını ve yirmi yaşında hukuktan en yüksek rütbeyi aldı. 1716 yılında öldüğünde ünü çok büyüktü.
I. Jean’ın ikinci oğlu Daniel (1700-1782), matematikçi oluncaya kadar doktorluk yaptı. Paris İlimler Akademisi ödülünü tam on kez kazandı. En ünlü eseri sıvılar dinamiğine aittir. Yirmi beş yaşındayken Saint Petersburg’a matematik profesörü olarak atandı. Anatomi, botanik ve fizik dersleri okuttu. Matematikte çok eser verdi. Daniel Bernoulli’ye, fiziğin kurucusu denilmiştir.
III. Nicolas, fiziğe çok çalıştı. Elde ettiği sonuçlar, Paris İlimler Akademisi ödülünü üç kez kazandıracak kadar parlaktı. Bu soyun yetenekleri bitmek tükenmek bilmez.
Galois (1811 - 1832)
Fransız matematikçisi Galois, 1811-1832 yılları arasında yaşadı. Abel'in çağdaşı olan bu matematikçinin doğum ve ölüm tarihlerine bakarsanız 21 yıllık bir ömür sürdüğünü görür ve bu işte bir yanlışlık olduğunu düşünebilirsiniz. Hiçbir yanlışlık yok. Galois'nın hayatı Brezilya dizilerine konu olmaya aday şanssızlıklarla sürüp gitmiş ve 21 yılda tükenmiştir.
Yakınları kendisinden söz ederken, annesinin erkek huylu, cömert, şerefli, açık bir şekilde alaycılığa kaçan ve bazen de çelişkilerde karar kılan bir kadın gibi anlatılıyordu. Anne, 1872 yılında seksen dört yaşında öldü. Aklını ve hafızasını ölünceye kadar korudu. O da, kocası gibi zulme, haksızlığa karşı bir öfke, kızma ve hınç besliyordu. Babası gibi, annesinin bu duyguları Galois da da görülür. Bu duygu ve düşüncelerden Galois da kurtulamamıştır. Onun kısa yaşamında bu duyguların etkisi çok büyük olmuştur.
Abel yoksulluktan ölmüştü. Galois ise, başkalarının budalalığından ölmüştür. İlim tarihi, en kaba budalalığın dehaya karşı zaferine, Galois'nın çok kısa süren hayatı kadar kusursuz ve eksiksiz bir örnek vermemiştir. Burada bir noktaya dikkat etmek gerekir. Galois bir melek değildi. Çok taşkındı ve derisine sığmıyordu. Bu onun yaramazlığından değil de, zekasının kafasının içine sığmamasındandı. O parlak yeteneği, aleyhine birleşmiş koyu bir budalalıkla boğulup gitti. Galois'nın her davranışı, taşan zekası ve onun dahi kafasının istediği yönde yönlendirilmediğinden ileri gelmiştir.
Galois'nın ne anne ve ne de baba tarafından matematiğe karşı en küçük bir yetenek görülmemiştir. Galois'nın matematik dehası, birden bire delikanlılık çağına doğru çıkmıştır. Galois, merhametli, acıyan, seven ve hatta ağır başlı bir çocuk olmakla beraber, babası şerefine düzenlenen toplantılarda ortamın neşesine katılmasını bilir ve konukları eğlendirmek amacıyla şiirler ve karşılıklı konuşma yazıları yazardı. Fakat, beceriksiz, yeteneksiz ve anlayışsız öğretmenlerinin rahatsız etme, canını sıkma ve tedirgin etmeleri, onların sersem ve pek akılsız davranışları yüzünden Galois'nın bu atılımları da çok sürmedi. Onu da hemen körelttiler.
Galois, 1823 yılında on iki yaşında Paris'teki Louis le Grand Lisesine girdi. Lise, kapıları sürgülü ve pencereleri demirli bir hapishaneden farksızdı. 1823 Fransa'sı daha Fransız devrimini unutmamıştı. Yöneticilerin, insanların ve bazı güçlerin tuzakları ve karşı tuzakları, ayaklanmalar ve ihtilal söylentileri sık sık görülen olaylardı. Olaylar tam oturmamış ve huzursuzluklar devam ediyordu. Toplumun bu huzursuzlukları Galois'nın lisesine de yansıyordu. Cizvitlerin yönetimi yeniden ele almasını sağlamak amacıyla lisenin müdürünün planlar hazırlamış olmasından kuşkulanan öğrenciler, kilisede bile okumayı, kabul etmeyerek ayaklandılar. Müdür, öğrenci ailelerine bile haber vermeden suçlu diye kuşkulandığı öğrencileri okuldan kovdu. Galois, bunların içinde değildi. Bulunsa herhalde Galois'nın geleceği için daha hayırlı olurdu. Çünkü, Galois, o güne kadar kanunsuz ve keyfi yönetimin, yalnız kelimesini biliyordu. Artık O, harekete geçmiş, kendisini olayların içinde bulmuştu. Ölünceye kadar da bu iz onda kalacaktır.
Boole (1815 - 1864)
2 Kasım 1815 yılında Lincoln'da doğan George Boole, basit bir dükkancının oğluydu. O çağın İngiltere'sinde dükkancılık oldukça aşağılanan bir meslekti. Kendi kendini yetiştiren bu dahinin yüksek zekası en aşağı halk tabakasına verilmişti. Bu zeka, kendi yağıyla kavrularak bulunduğu çevrede kalacaktı. Bu deha, yüksek tabakaların okullarında da okuyamazdı. Boole'un girmek istediği okulda Latince gibi lüks dersler de okutulmuyordu. Servet ve para yönünden daha aşağı düzeyde doğmuş olanların okulunda okumalıydı. Kendisinin fakirlikten hiçbir zaman kurtulamayacağını bilen ve oğluna kapalı kapıları açmak için elinden geleni yapmış olan babasının sevgiyle dolu ve cesaret verici sözleriyle Boole Latince'yi tek başına öğrendi. Bunun için babasının bir arkadaşı olan küçük bir kitapçıya başvurmuş, fakat bu adamcağız da çocuğa Latince'nin ilk gramer kurallarını açıklayabilmişti. Boole on iki yaşına geldiği zaman Horace'ın bir şiirini İngilizce'ye çeviri yapabilecek kadar Latince'yi öğrenmişti. Çeviri tekniğini bilmeyen baba, oğluyla gurur duyduğu için, bu çeviriyi bulundukları yerin yöre gazetesinde yayınlatır. Okulda büyük bir gürültü kopar. Bu gürültünün bir kısmı iyi ve bir kısmı da kötü yöndeydi.
Klasikler öğretmeni, on iki yaşındaki bir çocuğun böyle bir çeviriyi yapabileceğini bir türlü kabul etmiyordu. Bu çevirideki bazı yanlışlıklardan mahcup olan Boole, dilbilgisi eksikliklerini tek başına doldurmaya karar verdi. Bu sırada Yunanca'ya da başlamıştı.
Boole'un babası, oğluna okulunun üstünde matematik dersleri vermiş ve optik aletlerin yapımıyla ilgisini arttırmıştı. Fakat Boole, hala klasik çalışmalarının yüksek mevkilerin anahtarı olduğunu düşünüyordu. Okulu bitirdikten sonra ticaret derslerini izledi. Fakat, bu derslerin umduğu gibi bir faydası olmadı. On altı yaşına gelince fakir ailesine yardım etmek gerektiğini anladı. Bu nedenle de bir ilkokulda ders vermeye başladı. Bu öğretmenliği tam dört yıl sürdü. Fakat, rahat bir yaşama kavuşamamıştı. Serbest meslekte çalışmayı düşünüyordu. Asker ve hukukçu da olamazdı. İçinde bulunduğu öğretmenlikte pek iç açıcı değildi. Geriye papaz olmak kalıyordu. Dört yıllık öğretmenliği süresince Fransızca, Almanca ve İtalyanca dillerini de tam olarak öğrenmişti.
Sonunda Boole, tutacağı yolu buldu. Babasının ona vermiş olduğu ilk matematik dersleri artık meyvesini vermeye başlamıştı. Boole, yirmi yaşına gelince bir özel okul açtı. Burada matematik öğretmesi gerekiyordu. Babasından aldığı derslerin faydasını gördü. O zamanın el kitaplarını gözden geçirdi. Önce hayretle incelediyse de, sonra onlardan tiksindi. Acaba büyük matematikçiler neler yapmışlardı? Abel ve Galois gibi, büyüklerin kitaplarını okudu. Fazla bir matematik bilgisi olmayanların okuyup anlayamayacağı kesin olarak bilinen Laplace'ın "Gök Mekaniği" ni hiç kimsenin yardımı olmadan okuyup anladı. Lagrange'ın "Analitik Mekanik" adlı eserini tam anladı. Artık, kendisinin yolunu çizmişti. İlk ilmi çalışması olan değişim hesabı yayınlandı. Yine tek başına çalışmasının ürünü olan invaryantları keşfetti. Zaten bu invaryantlar olmasaydı, rölativite (bağlılık) kuramı olmazdı. Cebirsel denklemlerdeki boşlukları doldurdu.
Boole'un yaşadığı dönemde, bir dergide adamın olmadığı sürece bir çalışmanın yayınlatılması olanaksızdı. Boole, bu bakımdan şanslıydı. Çünkü, 1837 yılında, İskoçya'lı D.F.Gregory adında bir matematikçi , "Cambridge Mathematical Journal" adında bir dergi çıkarıyordu. Boole, derginin müdürüne çalışmalarının birkaçını verdi. Gregory bu çalışmaların orijinalliğini ve yazış biçimini çok beğendi. Yazıları yayınladı. Böylece, iki matematikçi arasında dostça bir arkadaşlık ve mektuplaşmalar başladı ve hayatları boyunca sürdü.
Modern cebir kavramı, Peacock, Herschel, De Morgan, Dabbage, Gregory ve Boole sayesinde yerini aldı. Boole, sembol ve işlemleri kullandı. Başlangıçta oldukça çok gürültü kopardı ama, sonunda yerine oturdu. Boole, de Morgan'ın hem hayranı ve hem de büyük bir dostuydu. İngiltere'deki büyük matematikçilerle ya kendisi doğrudan ya da mektupla haberleşiyordu. 1848 yılında "Mantığın Matematik Analizi" adlı bir çalışmasını yayınladı. Bu eser, matematikte yeni bir çığır açmış ve Boole da kesin bir üne kavuşmuştu. Bu broşür, de Morgan'ın da takdirlerini topladı. Bu eser, bundan altı yıl sonra ortaya çıkacak olan bir çalışmanın müjdecisi olacaktı.
Boole'a, Cambridge'e gidip eski temellere dayanan matematik derslerini okuması önerildi. O bunları dinlemedi. İki büklüm bir vaziyette ailesini geçindirmek için öğretmenliğe devam etti. Tüm bunlara karşın, araştırmaları ve konferanslarıyla ünü günden güne yayılıyordu. İrlanda'da Cork kentinde Queen's College yeni açılmıştı. Bu ün ona bu College'e 1849 yılında matematik profesörü olarak atanmasını sağladı. Fakirlikten gelen Boole, kendine açılan bu olanakların değerini bildi. Bu arada kayda değer eserler yayınladı. 1834 yılında, mantık ve olasılıklar üzerine büyük bir eser yayınladı. Bu sırada tam otuz dokuz yaşındaydı. Bu kadar derin orijinallikte bir eser meydana getirmesi için oldukça gençti. Sürekli çalışıyor ve yeni yeni buluşları gerçekleştiriyordu. Fakat, Boole'un bu matematiği uzun bir süre ilerletilmedi. 1910 ile 1913 Yılları arasında Whitehead ile Russel, Boole'un bu çalışmasını yeniden işlediler. Sembolik mantığın amansız düşmanı Cantor'dur. Bu kuramı çok eleştirmiştir. Halbuki, bu kuram onun kuramına da yardım ediyordu.
Eserlerinin yayınlanmasından sonra çok yaşamadı. Marie Everest ile evlendi. Gitmeye söz verdiği bir konferansa yetişmek için yağmurlu bir günde sırılsıklam olup yakalandığı bir zatürreden 8 Aralık 1864 günü elli yaşında öldü. Daha sonra karısı Marie Boole, onun fikirlerini içeren "Boole Psikolojisi" adı altında yayınlanan broşürde onu anlatır. O, çok büyük bir eser verdiğinin farkında olarak öldü.
Gauss (1777 - 1855)
Alman astronomu, matematikçisi ve fizikçisidir. Daha çocukluğunda, erken gelişmiş zekası, matematiğe karşı zekasıyla sivrildi ve Brounseweig dükünün ilgisini çekti. Dük, okul masraflarını üzerine alarak O' nu Göttingen Üniversitesine gönderdi. Henüz 16 yaşındayken Herschel'in 1781 de keşfettiği Uranüs gezegeninin yörünge elemanlarını hesaplayarak, Yer'in bir noktasından yapılan ölçülerle, bu gezegenin yörünge elemanlarını bulmaya yarayan ve günümüzde hala kullanılan bir metot ortaya koydu. 1798 de Helmesdt'e yaptığı bir inceleme gezisinden sonra, Braunschweig'a döndü ve birkaç yıl içinde kendisini büyük matematikçiler sırasına koyacak bir seri çalışma raporu yayımladı.
Sayılar üzerine incelemeleri topladığı Disqvisitiones Arithmetice'de (Aritmetik Araştırmalara) (1805), eşitlikleri, ikinci dereceden şekilleri, serilerin yakınsaklığını v.b. ele aldı. Piazzi tarafından 1810 da, küçük gezen Cerez'in keşfinden sonra Gauss, çeşitli gökmekaniği araştırmaları yaptı, hayatının sonuna kadar bağlı kalacağı Göttingen rasathanesine müdür oldu (1807) .Theoria Motus Corporum Coelestium İn Sectionibus Conicis Solem Ambientium (Konik kesitIi ? gökcisimlerinin güneş çevresindeki hareket kuramı) (1808) adlı ünlü eserini yazd1. Legendre ile hemen aynı zamanda düşündüğü ve daha önce 1797 de yararlandığı ?- en küçük kareler metodundan (1821) başka, yanılmalar teorisi ve iki terimli denklemlerin çözümü için genel bir metot buldu; uygun-tasvir üzerine araştırmalar, yüzeylerin eğriliği ve Disqvisitiones Generales Carca Sperficien Curvas'ta (eğri yüzeyler üzerine genel araştırmalar) (1827) , ispat ettiği ünlü teoremi de yazmak gerekir. Bu teoreme göre, bükülebilen fakat uzatılamayan bir yüzeyin eğriliği, yani eğriliklerinin çarpımı değişmez.
Göttingen ile Altona arasındaki meridyen yayının ölçülmesi sırasında (1821,1824), Gussu, geodezi çalışmalarında ışıklı işaretler verebilmek için, kendi adını taşıyan Helyotropu tasarladı. Optik alanında, eksene yakın ışık ışınları için düzenlenmiş merkezi optik sistemlerinin genel teorisini kurdu. Elektrikle özelIikle magnetizma ile ilgilendi, bu alanda magnetometreyi icat etti. Ve Resultate Aus Den Beabochtungen Des Manetischen Vereins (Yer magnetizmasının genel kuramı) (1839), adlı eserinde, magnetizmanın, matematik teorisini formülleştirdi. Suclides'ci olmayan hiperbolik geometrinin keşfinde, bu konuda hiç bir şey yayımlamamış olmakla birlikte, Gauss, Balyai ve Labocewsky'den önce çalışmalar yapmış ve başarı sağlamıştı.
ÜNLÜ TÜRK
MATEMATİKÇİLER
Ali Kuşçu
(1474-1525)

Türk İslam Dünyası astronomi ve matematik alimleri arasında, ortaya koyduğu
eserleriyle haklı bir şöhrete sahip Ali Kuşçu, Osmanlı Türkleri’nde,
astronominin önde gelen bilgini sayılır. “Batı ve Doğu Bilim dünyası onu 15.
yüzyılda yetişen müstesna bir alim olarak tanır.” Öyle ki; müsteşrik W
.Barlhold, Ali Kuşcu’yu “On Beşinci Yüzyıl Batlamyos’u” olarak adlandırmıştır.
Babası, Uluğ Bey’in kuşcu başısı (doğancıbaşı) idi. Kuşçu soyadı babasından
gelmektedir. Asıl adı Ali Bin Muhammet’tir. Doğum yeri Maveraünnehir bölgesi
olduğu ileri sürülmüşse de, adı geçen bölgenin hangi şehrinde ve hangi yılda
doğduğu kesinlikle bilinmektedir.
Ancak doğum şehri Semerkant, doğum yılının ise 15. yüzyılın ilk dörtte biri
içerisinde olduğu kabul edilmektedir. 16 Aralık 1474 (h. 7 Şaban 879) tarihinde
İstanbul’da ölmüş olup, mezarı Eyüp Sultan Türbesi hareminde bulunmaktadır. Ölüm
tarihi; torunu meşhur astronom Mirim Çele-bi’nin (ölümü, Edirne 1525) Fransça
yazdığı bir eserin incelenmesi sonucu anlaşılmıştır. Mezar yerinin 1819 yılına
kadar belirli olduğu ve hüsn-ü muhafazasının yapıldığı; ancak 1819 yılından
sonra, Ali Kuşcu’ya ait mezarın yerine, zamanının nüfuzlu bir devlet adamının
mezar taşının konmuş olduğu anlaşılmaktadır. Uluğ Bey’in Horasan ve
Maveraünnehir hükümdarlığı sırasında, Semerkant’ta ilk ve dini öğrenimini
tamamlamıştır. Küçük yaşta iken astronomi ve matema-tiğe geniş ilgi
duymuştur.
Devrinin en büyük bilginlerinden; Uluğ Bey , Bursalı Kadızade Rumi,
Gıyaseddün Cemşid ve Mu’in al-Din el-Kaşi’den astronomi ve matematik dersi
almıştır. Önce,Uluğ Bey, tarafından 1421 yılında kurulan Semerkant Rasathanesi
ilk müdürü, Gıyaseddün Cemşid’in, kısa süre sonra da Rasathanenin ikinci müdürü
Kadızade Rumi’nin ölümü üzerine, Uluğ Bey Rasathaneye müdür olarak Ali Kuşcu’yu
görevlendirmiştir. Uluğ Bey Ziyc’inin tamamlanmasında büyük emeği geçmiştir.
Nasirüddün Tusi’nin Tecrid-ül Kelam adlı eserine yazdığı şerh, bu konuda da
gayret ve başarısının en güzel delilini teşkil etmektedir. Ebu Said Han’a ithaf
edilen bu şerh, Ali Kuşcu’nun ilk şöhretinin duyulmasına neden olmuştur.
Kaynakların değerlendirilmesi sonucu anlaşılmaktadır ki; Ali Kuşcu yalnız telih
eseriyle değil, talim ve irşadıyle devrini aşan bir bilgin olarak tanınmaktadır.
Öyle ki; telif eserlerinin dışında, torunu Mirim Çelebi, Hoca Sinan Paşa ve
Molla Lütfi (Sarı Lütfi) gibi astronomların da yetişmesine sebep olmuştur. Bu
bilginlerle beraber, Ali Kuşcu’yu eski astronominin en büyük bilginlerinden
birisi olarak belirtebiliriz.
Cahit Arf
(1910-1997)

1910 yılında Selanik’te doğdu. Yüksek öğrenimini Fransa’da Ecole Normale
Superieure’de tamamladı (1932). Bir süre Galatasaray Lisesi’nde matematik
öğretmenliği yaptıktan sonra İstanbul Üniversitesi Fen Fakültesi’nde doçent
adayı olarak çalıştı. Doktorasını yapmak için Almanya’ya gitti. 1938 yılında
Göttingen Üniversitesi’nde doktorasını bitirdi. Yurda döndüğünde İstanbul
Üniversitesi Fen Fakültesi’nde profesör ve ordinaryus profersörlüğe yükseldi.
Burada 1962 yılına kadar çalıştı. Daha sonra Robert Koleji’nde Matematik
dersleri vermeye başladı.1964 yılında Türkiye Bilimsel ve Teknik Araştırma
Kurumu (Tübitak) bilim kolu başkanı oldu.
Daha sonra gittiği Amerika Birleşik Devletleri’nde araştırma ve incelemelerde
bulundu; Kaliforniya Üniversitesi’nde konuk öğretim üyesi olarak görev yaptı.
1967 yılında yurda dönüşünde Orta Doğu Teknik Üniversitesi’nde öğretim üyeliğine
getirildi. 1980 yılında emekli oldu. Emekliye ayrıldıktan sonra TÜBİTAK’a bağlı
Gebze Araştırma Merkezi’nde görev aldı. 1985 ve 1989 yılları arasında Türk
Matematik Derneği başkanlığını yaptı.
Arf İnönü Armağanı’nı (1948) ve Tübitak Bilim Ödülü’nü kazandı (1974). Cebir
ve Sayılar Teorisi üzerine uluslararası bir sempozyum 1990′da 3 ve 7 Eylül
tarihleri arasında Arf’in onuruna Silivri’de gerçekleştirilmiştir. Halkalar ve
Geometri üzerine ilk konferanslarda 1984′te İstanbul’da yapılmıştır. Arf,
matematikte geometri kavramı üzerine bir makale sunmuştur. Cahit Arf 1997
yılının Aralık ayında bir kalp rahatsızlığı nedeniyle aramızdan ayrıldı.
Kerim Erim
(1894-1952)

İstanbul Yüksek Mühendis mektebi’ni bitirdikten (1914) sonra Berlin
Üniversitesi’nde Albert Einstein’in yanında doktorasını yaptı (1919). Türkiye’ye
dönünce, bitirdiği okulda öğretim üyesi olarak çalışmaya başladı. Üniversite
reformunu hazırlayan kurulda yer aldı. Yeni kurulan İstanbul Üniversitesi Fen
Fakültesi’nde analiz profesörü ve dekan olduğu gibi Yüksek Mühendis Mektebi’nde
de ders vermeye devam etti. Yüksek Mühendis Mektebi İstanbul Teknik
Üniversitesi’ne dönüştürülünce buradan ayrıldı ve yalnızca İstanbul
Üniversitesi’nde çalışmaya devam etti. Daha sonra burada ordinaryüs profesör
oldu. 1948 yılında Fen Fakültesi Dekanlığı’na getirildi.
1940-1952 yılları arasında İstanbul Üniversitesi Fen Fakültesi’ne bağlı
Matematik Enstitüsü’nün başkanlığını yaptı. Türkiye’de yüksek matematik
öğretiminin yaygınlaşmasında ve çağdaş matematiğin yerleşmesinde etkin rol
oynadı. Mekaniğin matematik esaslara dayandırılmasına da öncülük etti. Matematik
ve fizik bilimlerinin felsefe ile olan ilişkileri üzerinde de çalışmalarda
bulunan Erim’in Almanca ve Türkçe yapıtları bulunmaktadır. Bunlardan bazıları
şunlardır:
Nazari Hesap (1931), Mihanik (1934), Diferansiyel ve İntegral Hesap (1945),
Über die Traghe-its-formen eines modulsystems (Bir modül sisteminin süredurum
biçimleri üstüne – 1928)
Ömer Hayyam
(1048-1131)

Asıl adı Giyaseddin Ebu’l Feth Bin İbrahim El Hayyam’dır. 18 Mayıs 1048′de
İranın Nişabur kentinde doğan Ömer Hayyam bir çadırcının oğluydu. Çadırcı
anlamına gelen soyadını babasının mesleğinden almıştır. Fakat o soyisminin çok
ötesinde işlere imza atmıştır. Daha yaşadığı dönemde İbn-i Sina’dan sonra
Doğu’nun yetiştirdiği en büyük bilgin olarak kabul ediliyordu. Tıp, fizik,
astronomi, cebir, geometri ve yüksek matematik alanlarında önemli çalışmaları
olan Ömer Hayyam için zamanın bütün bilgilerini bildiği söylenirdi. O herkesten
farklı olarak yaptığı çalışmaların çoğunu kaleme almadı, oysa O ismini çokça
duyduğumuz teoremlerin isimsiz kahramanıdır. Elde bulunan ender kayıtlara
dayanılarak Ömer Hayyam’ın çalışmaları şöyle sıralanabilir.
Yazdığı bilimsel içerikli kitaplar arasında Cebir ve Geometri Üzerine,
Fiziksel Bilimler Alanında Bir Özet, Varlıkla İlgili Bilgi Özeti, Oluş ve
Görüşler, Bilgelikler Ölçüsü, Akıllar Bahçesi yer alır. En büyük eseri Cebir
Risalesi’dir. On bölümden oluşan bu kitabın dört bölümünde kübik denklemleri
incelemiş ve bu denklemleri sınıflandırmıştır. Matematik tarihinde ilk kez bu
sınıflandırmayı yapan kişidir. O cebiri, sayısal ve geometrik bilinmeyenlerin
belirlenmesini amaçlayan bilim olarak tanımlardı. Matematik bilgisi ve yeteneği
zamanın çok ötesinde olan Ömer Hayyam denklemlerle ilgili başarılı çalışmalar
yapmıştır. Nitekim, Hayyam 13 farklı 3. dereceden denklem tanımlamıştır.
Denklemleri çoğunlukla geometrik metod kullanarak çözmüştür ve bu çözümler
zekice seçilmiş konikler üzerine dayandırılmıştır. Bu kitabında iki koniğin
arakesitini kullanarak 3. dereceden her denklem tipi için köklerin bir geometrik
çizimi bulunduğunu belirtir ve bu köklerin varlık koşullarını tartışır.
Bunun yanısıra Hayyam, binom açılımını da bulmuştur. Binom teoerimini ve bu
açılımdaki kat sayıları bulan ilk kişi olduğu düşünülmektedir. (Pascal üçgeni
diye bildiğimiz şey aslında bir Hayyam üçgenidir). Öğrenimi tamamlayan Ömer
Hayyam kendisine bugünlere kadar uzanacak bir ün kazandıran Cebir Risaliyesi’ni
ve Rubaiyat’ı Semerkant’ta kaleme almıştır. Dönemin üç ünlü ismi Nizamülmülk,
Hasan Sabbah ve Ömer Hayyam bu şehirde bir araya gelmiştir. Dönemin hakanı
Melikşah, adı devlet düzeni anlamına gelen ve bu ada yakışır yaşayan veziri
Nizamül-mülk’e çok güvenirdi. Ömer Hayyam ile ilk kez Semerkant’ta tanışan Nizam
onu İsfahan’a davet eder. Orada buluştuklarında O’na devlet hülyasından bahseder
ve bu büyük hayalinin gerçekleşmesi için Hayyam’dan yardım ister. Fakat Hayyam
devlet işlerine karışmak istemez ve teklifini geri çevirir. 4 Aralık 1131′de
doğduğu yer olan Nişabur’ da fani dünyaya veda eder.
Matrakçı Nasuh
(Bilinmiyor-1553)

Türk, minyatürcü. Ayrıca matematik ve tarih konularında kitaplar da yazmış
çok yönlü bir bilgindir. Doğum tarihi ve yeri bilinmiyor. Kâtip Çelebi ölüm
tarihi olarak 1533′ü vermekteyse de, bunun doğru olmadığı bugün kesinleşmiştir.
Çeşitli kaynaklarda onun 1547′den, 1551′den, 1553′ten sonra ölmüş olabileceği
ileri sürülmektedir. Yaşamı üstüne bilgi de yok denecek kadar azdır. Saraybosna
yakınlarında doğduğuna, dedesinin devşirme olduğuna ilişkin kesinleşmemiş
ipuçları vardır.
Enderun’da okumuştur. Matrakçı ya da Matrakî adıyla anılması, lobotu andıran
sopalarla oynandığı ve eskrime benzeyen bir tür savaş oyunu olduğu bilinen
“matrak” oyununda çok usta olmasından ve belki de bu oyunun mucidi bulunmasından
ileri gelmektedir. Nasuh ayrıca çok usta bir silahşördü. Bu nedenle Silahî
adıyla da anılırdı. Türlü silah ve mızrak oyunlarındaki ustalığı nedeniyle
Osmanlı ülkesinde “üstad” ve “reis” olarak tanınması için 1530′da I. Süleyman
(Kanuni) tarafından verilmiş bir beratı da vardı. Çeşitli silahların nasıl
kullanılacağını ve dövüş yöntemlerini anlatan Tuhfetü’l-Guzât adlı bir kılavuz
kitap bile yazmıştı.
Nasuh, özellikle geometri ve matematik alanlarında önemli bir bilim adamıydı.
Uzunluk ölçülerini gösteren cetveller hazırlamış ve bu konuda kendinden sonra
gelenlere önderlik etmiştir. Matematiğe ilişkin iki kitabı Cemâlü’l-Küttâb ve
Kemalü’l- Hisâb ile Umdetü’l-Hisâb’ı I. Selim (Yavuz) döneminde yazmış ve
padişaha adamıştır. Bu yapıtlardan sonuncusu uzun yıllar matematikçilerin
elkitabı olarak kullanılmıştır.
Gelenbevi İsmail Efendi
(1730-1790)

1730 yılında şimdiki Manisa’nın Gelenbe kasabasında doğan Gelenbevi İsmail
Efendi, Osmanlı İmparatorluğu matematikçilerindendir. Asıl adı İsmail’dir.
Gelenbe kasabasında doğduğu için ikinci adı onun bu doğduğu kasabadan gelir.
Daha çok Gelenbevi adıyla ün kazanmıştır. Önce, kendi çevresindeki bilginlerden
ilk bilgilerini almıştır. Daha sonra, öğrenimini tamamlamak üzere İstanbul’a
gitmiştir. Burada, çok değerli ve kültürlü öğretmenlerden yararlanıp matematik
bilgisini oldukça ilerletmiştir. Müderrislik sınavına kazananarak 33 yaşında
müderris olmuştur. Bundan sonra kendisini tümüyle ilme verip çalışmalarına devam
etmiştir.
Gelenbevi, eski yöntemle problem çözen son Osmanlı matematikçisidir. Sadrazam
Halil Hamit Paşa ve Kaptan-ı Derya Cezayirli Hasan Paşa’nın istekleri üzerine,
Kasımpaşa’da açılan Bahriye Mühendislik Okulu’na altmış kuruşla matematik
öğretmeni olarak atandı. Bu atama ona parasal yönden bir rahatlık getirdi.
Hakkında şöyle bir öykü anlatılır: ‘Bazı silahların hedefi vurmaması, padişah
III. Selim’i kızdırmış ve bunun üzerine Gelenbevi’yi huzuruna çağırarak ona
uyarıda bulunmuştur. Gelenbevi bunun üzerine hedefe olan uzaklıkları tahmin
ederek gerekli silahlardaki düzeltmeleri yapmış ve topların hedefi vurmalarını
sağlamıştır. Gelenbevi’nin bu başarısı padişahın dikkatini çekmiş ve padişah
tarafından ödüllendirilmiştir. Gelenbevi, Türkçe ve Arapça olmak üzere tam otuz
beş eser bırakmıştır. Türkiye’ye logaritmayı ilk sokan Gelenbevi İsmail
Efendi’dir.
Salih Zeki Bey
(1864-1921)

1864 yılında İstanbul’da yoksul bir ailenin oğlu olarak dünyaya geldi. Babası
Boyabatlı Hasan Ağa, annesi Saniye Hanımdır. Anne ve babasının ölümü üzerine
ninesi tarafından on yaşındayken Darüşşafaka’ya verildi. 1882 yılında
Darüşşafaka’yı birincilikle bitirdi. Aynı yıl Posta ve Telgraf Nezareti Telgraf
Kalemi (Fen Şubesi)’ne memur olarak atandı. 1884 yılında Nezaretin Avrupa’da
uzman telgraf mühendisi ve fizikçi yetiştirme kararı üzerine birkaç arkadaşıyla
birlikte Paris’e gönderildi ve burada Politeknik Yüksekokulu’nda elektrik
mühendisliği öğrenimi gördü. 1887 yılında İstanbul’a döndü ve eski dairesinde
elektrik mühendisi ve müfettiş olarak çalıştı. Ek görev olarak Mekteb-i
Mülkiye’de (bugün Ankara Üniversitesi’ne bağlı Siyasal Bilgiler Fakültesi) fizik
ve kimya dersleri verdi (1889-1900). Bu arada Rasathane-i Amire müdürlüğünde ve
II. Meşrutiyetin ilanından (1908) sonra Maarif Nezareti Meclis-i Maarif
üyeliğinde bulundu. 1910’da Mekteb-i Sultani (bugün Galatasaray Lisesi)
müdürlüğüne atandı. 1912’de Maarif Nezareti müsteşarı, 1913’te Darülfünün-ı
Osmani (bugün İstanbul Üniversitesi) rektörü oldu. 1917’de rektörlükten
ayrıldıysa da üniversitedeki görevini Fen Şubesi (Fakültesi) Müderrisi
(Profesör) olarak sürdürdü. Ömrünün sonuna doğru aklî dengesini kaybetti ve
tedavi altındayken 1921 yılında Şişli’deki Fransız Hastanesi’nde öldü. Fatih
Camiinin bahçesine gömüldü.
3 kez evlenmiş olan Salih Zeki, bu evliliklerden birini Halide Edip’le
(Adıvar) yapmış, ölümünden kısa bir süre önce ayrılmıştı. Salih Zeki, önde gelen
son dönem Osmanlı matematik bilginlerindendi. İkdam, Darüşşafaka ve İktisadiyat
gazeteleri ile Darülfünun dergisine sayısız katkıda bulundu. Dönemin ünlü
bilginleriyle matematik ve fen bilimleri konusunda yazılı tartışmalara girdi ve
bu konularda bir kısmı ders kitabı olmak üzere çok sayıda yapıt verdi.
Yapıtları: Hendese (Geometri) [lise ders kitabı]; Hikmet-i Tabiiye (Fizik)
[lise ders kitabı]; Mebhas-ı Savt (Fonetik); Mebhas-ı Elektrik-i Miknatisi
(Elektro Magnetizma); Mebhas-ı Hararet-i Harekiye (Termodinamik); Mebhas-ı
Cazibeyi Umumiye (Genel Çekim); Mebhas-ı Elektrikiyet ve Şariyet (Elektrik ve
Kılcallık); Hesab-ı İhtimali (İhtimaller Hesabı); Mebhas-ı Hareket-i Seyalat
(Akışkanların Hareketi); Hendese-i Tahliliye (Analitik Geometri); Mebhas-ı
Nazariye-i Temevvücat (Dalga Teorisi); Heyet-i Riyaziye (Matematik Astronomi);
Kamus-u Riyaziyat (Matematik Ansiklopedisi); Asar-ı Bakiye (Ölmez Eserler). Son
iki yapıtın tamamı, ayrıca Henri Poincare’den çevirdiği dört kitap
basılmamıştır.
Masatoşi Gündüz İkeda
(1926-2003)

Cebirsel sayılara katkılarıyla tanınan Japon asıllı Türk matematik bilgini.
1948′de Osaka Üniversitesi Matematik Bölümü’nü bitirdi. 1953′te doktor, 1955′te
de doçent unvanlarını aldı. 1957-59 arasında Almanya’da Hamburg Üniversitesi’nde
Helmuth Hasse’nin yanında araştırmalar yaptı. Hasse’nin önerisi üzerine 1960′ta
Türkiye’ye gelerek Ege Üniversitesi Tıp Fakültesinde İstatistik dersleri vermeye
başladı. 1961′de aynı üniversitenin fen fakültesinde yabancı uzmanlığa atandı.
1964′te Türk uyruğuna geçerek, 1965′te doçent, 1966′da profesör oldu. 1968′de
Ege Üniversitesi’nin izniyle bir yıl süreyle çalışmak üzere Orta Doğu Teknik
Üniversitesi’ne gitti. İzninin bitiminde Orta Doğu Teknik Üniversitesi’nin
sürekli kadrosuna girdi. Çeşitli tarihlerde Hamburg, ABD’deki California ve
Ürdün’deki Yermuk üniversitelerinde konuk öğretim üyesi,1976′da Princeton’daki
Yüksek Araştırma Enstitüsü’nde araştırmacı olarak çalıştı. Türkiye Bilimsel ve
Teknik Araştırma Kurumu’nun (Tübitak) Temel Bilimler Araştırma Kurumunda yer
aldı. Orta Doğu Teknik Üniversitesi Pür Matematik Araştırma Ünitesi başkanlığı
yaptı. Cebir ve sayılar kuramına katkılarından dolayı 1979′da Tübitak Bilim
Ödülü’nü kazandı. Japonya’da bulunduğu dönemde halkalar kuramı ve grupların
matrisle gösterimi üzerine araştırmalar yapan İkeda, 1970′lerde cebirsel sayılar
kuramına yönelerek, rasyonel sayılar cisminin salt Galois grubunun
otomorfizimleri ve tümelliği konularında önemli çalışmalar gerçekleştirdi. Ünlü
matematik dergisi Crelle’s Journal’da yayımlanan bir çalışmasında Galois
grubunun çok özel bir yapıda olduğunu gösterdi.
Ali Nesin
(1956-)

1956′da İstanbul’da doğdu. İlkokuldan sonra ortaokulu İstanbul’da Saint
Joseph Lisesi’nde, liseyi de İsviçre’nin Lozan kentinde tamamlayan Nesin
1977-1981 yılları arasında Paris VII Üniversitesi’nde matematik öğrenimi gördü.
Daha sonra ABD’de Yale Üniversitesi’nde matematiksel mantık ve cebir konularında
doktora yapan Ali Nesin, 1985-1986 arasında Kaliforniya Üniversitesi Berkeley
Kampusü’nde öğretim üyeliği yaptı. Türkiye’ye kısa dönem askerlik görevi için
geldiği sırada “orduyu isyana teşvik” iddiasıyla tutuklanarak yargılandı.
Yargılanma sonunda beraat ettiği halde pasaport verilmediği için işine dönemeyen
Nesin, sonunda yeniden passaport alarak yurtdışına gitti. 1987-1989 arasında
Notre Dame Üniversitesi’nde yardımcı doçent, ardından 1995′e kadar Kaliforniya
Üniversitesi Irvine Kampusü’nde doçent ve daha sonra profesör olarak görev
yaptı. 1993-1994 Öğretim Yılı’nı Bilkent Üniversitesi’nde misafir öğretim
görevlisi olarak geçirdi. 1995′te, babası Aziz Nesin’in ölümü üzerine yurda
kesin dönüş yaptı ve Nesin Vakfı yöneticiliğini üstlendi. Ayrıca Bilgi
Üniversitesi Matematik Bölümü Başkanı olan Ali Nesin iki çocuk sahibidir. Kasım
2004′den beri de Nesin Yayınevi genel yönetmenliğini yapmaktadır.
Ali Nesin’in Matematik ve Korku, Matematik ve Doğa, Matematik ve Sonsuz,
Develerle Eşekler, Önermeler Mantığı adlı kitaplarının yanısıra çeşitli
dergilerde çıkmış bilimsel makaleleri ve İngilizce bir kitabı bulunmaktadır.
Matematiksel araştırma alanı “Morley mertebesi sonlu gruplar”dır. Aynı zamanda,
üç ayda bir yayımlanan, Matematik Dünyası adlı bir matematik dergisi
çıkarmaktadır.
Matematik araştırmaları, bölüm başkanlığı ve Nesin Vakfı yöneticiliğinin yanı
sıra yağlıboya resim, desen ve portre çalışmaları da yapmaktadır.
8.Sınıf 2009 SBS'de çıkmış soruları buradan pdf formatında açabilirsiniz.

8.Sınıf 2009 SBS'de çıkmış soruları buradan pdf formatında açabilirsiniz.

8.Sınıf 2010 SBS'de çıkmış soruları buradan pdf formatında açabilirsiniz.


8.Sınıf 2010 SBS'de çıkmış soruları buradan pdf formatında açabilirsiniz.
8.Sınıf 2011 SBS'de çıkmış soruları buradan pdf formatında açabilirsiniz.

8.Sınıf 2011 SBS'de çıkmış soruları buradan pdf formatında açabilirsiniz.

MATEMATİK FIKRALARI

KAÇ KİŞİ VAR?
Bir matematikçi, bir fizikçi ve bir biyolog bir kafeye oturmuş karşıdaki eve bakarlarken eve iki kişi girdiğini görürler. Bir müddet sonra evden üç kişi çıktığını gördüklerinde olayı şu şekilde yorumlarlar. Fizikçi: Gözlem hatası yaptım. Biyolog: İçerde ürediler. Matematikçi: Eve bir kişi daha girerse içerde hiç kimse kalmayacak.
DENEY
Bir matematikçi, bir fizikçi ve bir kimyacıyı bir ay süreliğine ayrı ayrı odalara kapatmışlar. Odalarda kilitli bir buzdolabı ve çeşitli araç gereç varmış. Bir ay sonunda odaların kapılarını açıp bakmışlar. Fizikçi mekanik bir makine yaparak buzdolabının kapısını kırmış ve karnını doyurmuş. Kimyacı çeşitli elementleri karıştırarak bir sıvı yapıp buzdolabının kapısını eritmiş. Son olarak matematikçinin odasına girmişler. Matematikçinin kurumuş cesedi duvara dayanmış bir halde yerde kanla şunlar yazılıymış. Teorem: Buzdolabını açamazsam ölürüm. İspat: Buzdolabını açtığımı varsayalım.
MATEMATİKÇİ
Balonla seyahat etmekte olan bir grup yolunu kaybeder ve biraz alçalarak aşağıdaki kişiye yaklaşırlar. İçlerinden biri aşağıya bağırır: - Heyyy!.. Şu anda nerdeyiz? Aşağıdaki şahıs onlara şöyle bir bakar ve biraz düşünüp dalgın dalgın cevap verir: - Bir balonun içinde ve oldukça alçaktasınız…Balondaki adam doğrulur ve arkadaşlarına: - Biliyor musunuz bu adam matematikçi der. Bunun üzerine balondaki diğer şahıslar bunu nerden anladığını sorduklarında şöyle yanıtlar: - Birincisi, çok düşündü, ikincisi söylediği şey kesin olarak doğru… Üçüncüsü, bir işe yaramıyor…
Bir matematik öğrencisi finale çalışamamıştır ve sınava girdiğinde bakar ki sorular doğru/yanlış tipinde. Ne yapacağı bellidir. Çıkarır bir bozuk para ve yazı-tura atarak imtihanı cevaplandırmaya başlar. Gözetmen de bir yandan takip etmektedir onu. Bu şekilde iki saat geçer. Herkes sınıfı terketmiştir fakat o hala yazı tura atmaktadır. Gözetmen dayanamaz ve gelip sorar: - Sınava çalışmadığın ortada. Kitapçığı bile açmadın ve yazı-tura atarak cevaplandırıyorsun. Peki seni bu kadar uzun süre meşgul eden nedir? Öğrenci hiç istifini bozmaz ve bozuk parayı fırlatmaya devam eder: - Şşşt, cevapları kontrol ediyorum.
TÜREV
Birgün birkaç fonksiyon bir kafede oturmuş, sıfıra ne kadar hızla yakınsadıkları gibi konular üzerinde tartışıyorlarmış. Derken içlerinden biri kapıya bakarak aniden bağırmış “Dikkat türev geliyor!”. Hepsi apar topar sandalyelerinin altına saklanmışlar, ancak ex hiç istifini bozmamış. Türev yavaş yavaş içeri girmiş ve tek başına oturan fonksiyonu görüp “sen benden korkmuyor musun?” demiş. Hayır, ben ex’im diye yanıtlamış kendine güvenen bir tavırla. “Yaa” demiş türev. “Peki benim x’e göre türev alacağımı kim söyledi?”
UÇAK YOLCULUĞU
İki Matematikçi bir uçak seyahatine başlarlar. Havalandıktan bir saat sonra bir anons duyulur; - Sayın yolcularımız. Uçağımızın dört motorundan biri arızalanmıştır. Endişe etmeyiniz. Üç motorla uçuşu tamamlayabiliriz. Fakat beş saat sürecek yolculuğumuz yedi saate uzamıştır.Yola devam ederler. Kısa bir süre sonra yeni bir anons duyulur; - Sayın yolcularımız. Uçağımızın sağlam olan üç motorundan biri arızalanmıştır. Endişe etmeyiniz. İki motorla uçuşu tamamlayabiliriz. Fakat yolculuğumuz on saate uzamıştır.Derken az bir vakit sonra üçüncü anons duyulur; - Sayın yolcularımız. Motorlarımızdan biri daha arızalanmıştır. Fakat paniğe kapılmayınız.Tek motorla da uçuşu tamamlayabiliriz. Ancak yolculuğumuz on sekiz saate uzamıştır.Bu son anons üzerine Matematikçilerden biri şöyle der;- Umarım bu son motor da arızalanmaz. Yoksa sonsuza kadar burada kalacağız.
İSKOÇ KOYUNLARI
Bir mühendis, bir fizikçi ve bir matematikçi İskoçya'da trenin penceresinden bakarken siyah bir koyun görürler, mühendis hemen atılır
- İskoçya'daki tüm koyunlar siyah.
der. Fizikçi söze karışır
- İskoçya'daki bazı koyunlar siyah.
der ve matematikçi son noktayı koyar:
- İskoçya'da en az bir tarafı siyah olan en az bir tane koyun vardır.
YARDIM TALEBİ
Çocuk babasından matematik ödevini yapmasına yardım etmesini ister ve
- Doğru olmaz oğlum, cevabını alır fakat o ısrarlıdır:
- En azından dene baba...
AZİM
İskoçlu bir matematikçi yolda giderken bir nal bulur ve sevinç içinde şöyle der:
- Geriye kaldı üç nal, bi at!..
NAZİ KAMPI
Hitler birgün kamplardan birini ziyaret ederken oradaki tutuklulardan birine sorar:
- 5, 3 daha kaç eder?
Mahkum 6 diye cevap verdiğinde yanındaki kurmaya döner ve kızgın bir ses tonuyla:
- Ne biçim toplama kampı bu?.. diye azarlar.
iNDiRGEME
Bir matematikçi ve fizikçi fakültenin dinlenme salonun da oturup kahvelerini yudumlarken bakarlar ki kahve makinesi tutuşmuş, fizikçi hemen koşarak eline aldığı kovayı doldurarak ateşi söndürür.ikinci gün olacak ya aynı olay tekrar vuku bulur.Bunun üzerine matematikçi koşar kovayı alır getirir ve fizikçinin eline tutuşturarak problemi daha önce çözümlenmiş olanına indirger.
YANGIN
Bir mühendis ,bir fizikçi ve bir matematikçi bir oteldedir. Derken mühendis burnuna gelen duman kokusuyla uyanır,hole çıkar, bir de bakar ki bir yangın var. Eline geçirdiği bir kovaya su doldurarak yangını söndürmeye çalışır.Daha sonra fizikçi uyanır, aynı yangını görür ve yangın hortumunu bulur ve başlar hesap yapmaya; su basıncı, alevin şiddeti,aradaki mesafe falan derken hesaplara göre minimum miktarda suyla ve minimum enerjiyle yangını söndürür (ikinci versiyon yaptığı hesaplara göre yangının sönmeyeceği ortaya çıkar ve yatağına geri döner)Daha sonra matematikçi kalkar kokunun etkisiyle ve hole koşar bir de baksın yangın var.Derken çözüm aramaya koyulur.Derken yangın hortumunu bulur ve “çözümü buldum” diye bağırarak yatağına geri döner.
ÜÇGENiN TANIMI
İlkokulda, matematik dersinde öğretmen üçgenin alanını,çocuklara
şu şekilde öğretmiş: Bir üçkenarlının alanı, yatayımı ile dikleşiminin
vuruşumunun, ikiye bölümüdür. Çocuk bunu güzelce ezberlemiş.
Aksam babası evde sormuş:
- Bu gün okulda ne öğrendiniz?
- Matematik dersinde, bir üçkenarlının alanını öğrendik babacığım.
- Ya öyle mi, peki nasıl öğrendiniz?
- Bir üçkenarlının alanı, yatayımı ile dikleşiminin vuruşumunun,
ikiye bölümüdür.
- Yavrum, yanlış öğretmişler size. Doğrusu : Bir üçgenin alanı,
tabanı ile yüksekliğinin çarpımının yarısına eşittir.
O sırada, bir yandan gazetesini okuyan, bir yandan da torunuyla
oğlunun konuşmasını dinleyen dede, dayanamayıp söze girmiş :
- İkinizin de tanımı yanlış! Bir müsellesin mesaha-i sathiyesi,
kaidesiyle irtifaının hasıl-ı darpının nısfına müsavidir.
TASAVVUR
Bir matematikçi ve bir mühendis ünlü bir fizikçinin seminerine katılırlar. Seminer Kulza-Klein teorisi üzerinedir ve 9 boyutlu uzayda cereyan eden bir takım işlemler içermektedir. Matematikçinin seminerden oldukça keyif alır görünmesine karsın, mühendis çok zorlanmaktadır. Başı çatlayacak derecede ağrımaya başlayınca dayanamaz sorar:
- Bu garip ve zor şeyleri nasıl anlayabiliyorsun?
Matematikçi gayet sakin cevap verir:
- Sadece olayı tasavvur ediyorum.
- 9 boyutlu bir uzayı nasıl tasavvur edebilirsin ki?
- Aslında çok kolay. Sadece n boyutlu bir uzay tasavvur ediyorum. Daha sonra n ' yi 9'a götürüyorum.
MESLEK SEÇiMi
İki arkadaş hangi mesleği seçmeleri gerektiğine bir türlü karar veremezler ve bir danışmana giderler.
Danışman bunların problem çözme yeteneklerinin oldukça iyi olduğunu fark eder ve şöyle bir deney yapar: içinde bir gaz ocağı, bir masa ve masanın üstünde bir çaydanlık bulunan iki ayrı odaya onları sokar ve suyu kaynatmalarını ister. iki adam da aynı şekilde masanın üstünden çaydanlığı alıp ocağa koyar ve ocağı yakar. Danışman daha sonra onları aynı şekildeki iki ayrı odaya sokar fakat bu sefer
çaydanlıklar masanın üstünde değil, yerdedir. iki arkadaştan biri çaydanlığı yerden alır, ocağa koyar ve ocağı yakar. Danışman ona mühendis olmasını, çünkü her problemi ayrıca çözme yeteneğine sahip
olduğunu söyler. Diğer şahıs ise çaydanlığı önce masanın üstüne koyar, daha sonra masanın üstünden alıp ocağa koyar ve ocağı yakar. Danışman ona ise matematikçi olmasını, çünkü problemi daha önce çözülmüş bir probleme indirgediğini söyler.
KAYIP ANAHTARLAR
Bir pür, diğeri uygulamalı matematikçi olan iki kişi arabalarından inerler ve benzer şekilde elli metre yürüdükten sonra arabalarının anahtarlarını kaybettiklerini fark ederler. Uygulamalı matematikçi arabasının yanına döner ve arabasının yanından tekrar başlayarak gitmiş olduğu yolu arar ve anahtarlarını bulur. Pür matematikçi ise yolun karanlık olmasından dolayı diğer uçtaki daha aydınlık bir yere gider ve anahtarlarını orada arar.
SEVGiLi Mi, EŞ Mi?
Bir doktor, bir avukat ve bir matematikçi konuşurlarken aralarında sevgilinin mi yoksa eşinin mi olmasının daha iyi olduğu şeklinde bir tartışma başlar. Avukat der ki:
- Tabii ki sevgilin olması daha iyidir. -istediğin zaman ayrılabilirsin, halbuki evli olursan bir sürü hukuki sorumluluk biner tepene.
Doktor buna muhalefet eder:
- Evli olmak daha iyidir. Çünkü güvenlik hissi stresi azaltır ve daha sağlıklıdır.
Matematikçi ise bambaşka telden çalmaktadır:
- Bence ikisi de olmalı. Bu şekilde karın seni sevgilinle ve sevgilin de karınla zanneder. Sende bu arada rahatça matematikle uğraşabilirsin.
2x2 KAÇ EDER?
Trabzon'un en zengininin oğlu olan Temel matematik dersinden sürekli çakıyormuş. Hocası son sınavı tezahüratla ona moral verilsin diye Avni AKER stadında yapmaya karar vermiş. Stad tıklım tıklım dolmuş. -izleyenler Temel'e müthiş tezahürat yapıyorlarmış. Hocası kolay bir soruyla başlayayım demiş ve:
- 2 kere 2 kaç eder?..
diye sormuş. Temel düşünmüş düşünmüş ve:
- 4 eder...demiş.
Statta derin bir sessizlik olmuş. Ardından bütün stad hep bir ağızdan:
- Hocam, pi şans daha!..







SORULAR:
1-Uzadıkça kısalan şey nedir?
2-Ali, sepetteki elmaların yarısını ve bir yarım elmayı Ayşe'ye; sonra kalan elmaların yarısını ve bir yarım elmayı Ahmet'e ve yine kalan elmaların yarısını ve bir yarım elmayı da Hasan'a veriyor. Sonuçta sepette sadece bir elma kaldığına göre başlangıçta kaç elma vardı?
Not: Elmalar bölünmeden paylaşılıyor.
3- Bir avcı otobüse binmek ister. Yalnız, otobüse boyutları en fazla 1mt. olan eşyalar alınmaktadır. Avcının tüfeği ise 1,5 mt.dir. Tüfeğin şeklini bozmamak şartı ile otobüse nasıl biner?
4-Bir tabakta 7 tane portakal var. Bu portakalları, 7 çocuğa birer tane bütün portakal vererek paylaştırın ve hâlâ tabakta bir portakal kalsın?
5- Dünyanın çevresini ekvatordan geçecek şekilde bir ip ile bağladığımızı kabul edelim.(yaklaşık 40 bin km.) Bu ipi her noktadan 1mt. havada tutabilmek için, ne kadar daha ip ilave etmeliyiz?
6- 6 adet kibrit çöpü ile 4 adet 'eşkenar üçgeni' nasıl elde edebiliriz?
7- Bir duvarın üzerinde 5 adet kuş duruyor. O sırada oradan geçmekte olan bir avcı, tüfeğini ateşleyip ikisini vuruyor. geriye kaç kuş kalır? (Cevap 'hiç' değil)
8- İki kişi yolda karşılaşıyorlar. Küçük olan, Büyüğün öz oğludur. Ancak büyük olan küçüğün babası değildir. Bu nasıl olur?
9- Bir çocuk, 7 elmanın ikisi hariç hepsini yerse, kaç elma kalır?
10- Bir satranç tahtasında kaç tane 'kare' vardır? ( 64 değil !)
11-
Yılın kaç ayında 'otuz' gün vardır?
12- Ali ile Veli 100 metre yarışı yapıyorlar. Ali, Veli'yi 5 metre farkla geçiyor. Yani Ali yarışı bitirdiğinde Veli 95. metrededir. Tekrar yarışmaya karar veriyorlar. Fakat bu sefer Ali, başlangıç çizgisinden 5 metre geriden başlıyor. Aynı hızla koştuklarını kabul edersek bu yarışı kim kazanır?
13- B - İ - Ü - D - ?
Soru işareti yerine hangi harf gelmelidir?
14- A, B, C, D VE E birbirlerinden ve sıfırdan farklı tamsayılardır.
ABCDE x 4 = EDCBA ise A=? B=? C=? D=? E=?
15- 2 + 2 + 2 = 244 Bir işareti değiştirerek eşitliği sağlayın.
16- Bir tüccar, sattığı mala %10 zam yapar. Ancak zamdan sonra satışlar düşmeye başlar. Fiyatı, yeni fiyatın %10 altına çeker. İlk duruma göre kârda mıdır, zararda mıdır?
17- Üç kedi, üç fareyi üç dakikada yakalarsa dokuz kedi, dokuz fareyi kaç dakikada yakalar?
18- 2 - 8 - 18 - 32 - 50 - ?
19- Bir tartı aletinde iki kutu ayrı ayrı tartılıyor. İlk kutu 5kg, ikinci kutu da 6kg geliyor. İki kutu beraber tartıldığında ise ibre, 12kg'ı gösteriyor. Yanlış tartıldığı belli olan kutuların gerçek ağırlıkları nedir?
20- Bir kalem ve bir silginin toplam fiyatı 110 TL'dir. Kalem, silgiden 100 TL daha pahalı olduğuna göre herbiri kaçar liradır? (Cevabı akıldan veriniz)
CEVAPLAR:
1- Hayat veya Ömür.
2- 15 elma
3- Avcı tüfeğini boyutları 1 mt. olan bir kutuya koyar. Küpün en uzak iki köşesinin uzunluğu, yaklaşık 1.73 mt. dir. ıÜü4- Son
4- Son kalan çocuğa portakal, tabakla birlikte verilir.
5- 6,28 mt. Çapı 40bin km. olan bir daire düşünürsek, yarıçapı sadece 1 mt. arttırmamız gerektiği anlaşılır. (Çevre=2pr ise r yerine (r+1) yazılır. O da 2p farkeder.)
6- Üçgen Piramit.
7- Vurulan 'iki' kuş kalır. Diğerleri kaçar
8- Demekki 'annesi'dir.
9- İkisi hariç ise tabi ki 'iki' tane kalır.
10- 204 kare vardır. Bütün 1x1(64 adet), 2x2(49 adet), 3x3(36 adet), 4x4(25 adet), 5x5(16 adet), 6x6(9 adet), 7x7(4 adet), 8x8(1 adet) ölçülerindeki kareler 204 tanedir.
11- Şubat hariç bütün aylarda 'otuz' gün vardır.
12- Ali, Veli'ye 95. metrede yetişeceğinden, son 5 metreyi, hızlı olan Ali önde bitirir.
13- Bir, İki, Üç, Dört, Beş...( Yani B).
14- A=2 - B=1 - C=9 - D=7 - E=8.
15- +'lardan birini 4 yaparız.
16- %1 zarardadır.
17- 'Üç' Çünkü herbirine bir fare düşer.
18- 72 (Genel terim:2n²)
19- İlki 6, ikincisi 7 kg
20- Kalem=105 YTL, silgi=5 YTL
Matematik İle İlgili İlginç Bilgiler
Matematik VE HAYAT Toplayalım çift sayfalar acıları, karşısına Kocaman BİR eşittir koyup hayatımızın terazisinde neye denk geliyor anlayalım. Anlayalım hiçe sayanları almayı nefes. Yada tam tersini yapalım işlemin. Bizi nefes almaktan vazgeçirecek acılarımızı toplamaya çalışalım. Ayşe anlamsız BİR Değer alıştırması. Hayatın neresinde olursak olalım. Hangi pencerenin ardından baktığımızla alakası olmayan BİR sonuç bulacağız. Ki sağlıklı düşünen hiçbir Beyin wanna know Ve bilmek bulamayacak nefes almasına engel olacak BİR acılar toplamı ... Kucaklaması Öğrenciler matematiğin günlük Hayatta ne işlerine yarayacağından bahseder dururlar. Oysa hayatın değerlendirmesini de, eksileri ve artılarıyla düşünür, matematikle yorumlarız. Sorunlarımızı farklı yollardan çözmeye çalışır, çözdüğümüz sorunlarımızın etrafında dönmez sağlamasını yaparız. X ve Y ler yine hayatımızın tam ortasında dururlar. Eşitlik ve eşitsizlik günümüzün Temel sorunlarından. Kısacası öyle Tense'lerde Boyle matematikle yaşarız, matematikle soluk alıp veririz. Matematiği sayılardan. Elle tutulur gözle görülür somut kavramlardan ibaret saymak elbette hayatımızda onun etkisinden bihaber olmamıza neden olacaktır. Duygularımıza hükmeden matematik sistemini çözemediğimiz sürece, çift sayfalar eşittirlerin sağına mutluluğum cümlesini yazıp İşleme Devam etmediğimiz sürece, yaşamın bize Adil davranmadığına Dair BİR cok cümle kuracağız. Birçok bilinmeyenli denkleme dönüşen yaşantımızı BİR Gün sadeleştirmek istediğimizde yapılan çift sayfalar işlemleri karşımıza alıp bakacağız. Sadeleştirmelere, o günün bilinmeyenlerine, kendi bilgisizliğimize. Ayşe Gün cok kolayca çözebildiğimiz denklemleri o günlerde nasılda kavrayamadığımıza BİR türlü anlam veremeyeceğiz. ? = Mutluluğum Ayşe sorunun çift sayfalar Çözümleri etrafında dönmez doğruları yapmamızı sağlamayacaktır elbette. Ama çözümü yaparken duygularımızın ve mantığımızın İşleme olan etkilerini iyi ayarlayabilirsek küsüratlıda öndeydi istediğimize YAKIN BİR sonuç elde ederiz. Yaptığımız çift sayfalar met işlemlerin puanlamasını Yapan vicdanımız imkb wanna know Ve bilmek yanılmayan BİR hesap makinesidir. Sağlamaları onunla yapmak ve hataları tekrarlamamak eminim mutluluğa ulaşmamızı kolaylaştıracaktır. Toplama ve çarpma işlemlerine takılmadan. Çıkarma ve sadeleştirme işlemlerinin ne kadar değerli olduklarını unutmadan yaşamaya çalışırsak, bizi nefes almaktan vazgeçirecek çift sayfalar sorun toplamlarının değersizliğini hayat doğrusunda kolayca görebiliriz. |
Matematik ile ilgili sözler
"İnsanoğlunun değeri bir kesirle ifade edilecek olursa; payı
gerçek kişiliğini gösterir, paydası da kendisini ne zannettigini,
payda büyüdükçe kesrin değeri küçülür."
TOLSTOY
"Başka herşey de oldugu gibi matemetiksel bir teori için de öyledir;
güzellik algılanabilir fakat açıklanamaz."
Cayley, Arthur
"Gerçeği aramak onu elde etmekten daha kıymetlidir."
Einstein, Albert
"Hayat sadece iki şey için güzel;matematiği keşfetme ve öğretme"
Simeon Poisson
Sık sık "matematik, teoremleri isbatlamaktan ibarettir" sözünü işitiriz.
Bir yazarın temel işi cümle yazmak degil midir?
Rota, Gian-carlo
"Aptalların sorup akılı insanların cevap veremediği pek çok soru vardır."
Polya, George
"Matematikle ifade edebiliyorsanız, bilginiz doyurucudur."
Lord KELVIN
"Mekanik matematiksel ilimlerin cennetidir, çünkü kişi onunla matematiğin
meyvelerine ulaşır."
"Akıllarımız sınırlı, fakat bu sınırlılığın şartları içersinde sonsuz
olasılıklarla çevrilmişiz. İşte hayatın gayesi bu sonsuzluktan
kavrayabildiğimiz kadar çok şey kavramak."
Whitehead, Alfred North
"Evren matematik dilinde yazılmıştır ve insan olarak onda yazılan kelimeleri matematik olmaksızın anlamamız imkansızdır"
Galileo, 1623
"Ben matematikten anlamam demek,benim kafam pek çalışmaz demenin başka türlüsüdür"
Gülay Göktürk
"Sen de biliyorsun ki biz hepimiz aynı sebepten dolayı matematikçi
olduk; tembeliz."
Rosenlicht, Max
"matematik bilmeyen giremez "
Ünlü filozof Aristo açtığı okulun kapısına yukarıdaki yazıyı asmıştır."
Bir matematikçi sanmaz fakat bilir.ınandırmaya çalısmaz çünkü ispat eder.Güveninizi beklemez.Belki dikkat etmenizi ister.
Henri POINCARE
Matematiği kullanmayan bilimler, ele aldıkları konularda ancak dış yapıyı inceleyebilirler; çünkü matematikle dile getirdikleri, ancak birtakım bağıntılardır; bu bağıntılar ise özle ilgili unsurlar arasında değil, dış görünüşle ilgili noktalar arasında olabileceğinden, bir varlığın özünü, onun aslında ne olduğunu bize vermekten acizdirler. O halde matematik, tabiat bilimleri, tarih gibi kişiliğin içlerine nüfuz edip, onu derin bir sezgi ile kavrayabilen bir disiplinin önünde çok aşağı niteliktedirler.
M. Kemal Atatürk
“Dünyadaki en mâsum uğraş matematiktir”
G. H. HARDY
“...evren her an gözlemlerimize açıktır; ama onun dilini ve bu dilin yazıldığı harfleri öğrenmeden ve kavramadan anlaşılamaz. Evren matematik diliyle yazılmıştır; harfleri üçgenler, daireler ve diğer geometrik biçimlerdir. Bunlar olmadan tek sözcüğü bile anlaşılamaz; bunlarsız ancak karanlık bir labirentte dolanılır.”
GALİLEO
Bilim deyince, onda hakikat diye öne sürdüğü önermelerin pekin olmasını ister; pekinlik ise en mükemmel şekliyle matematikte bulunur. O halde bilim o disiplindir ki; önermeleri matematikle ifade edilir. O zaman matematiği kullanmayan disiplinler bilimin dışında kalacaklardır.
M.Kemal Atatürk
“İnsanlar sayılar gibidir, o insanın değeri ise o sayının içinde bulunduğu sayı ile ölçülür.”
NEWTON
Matematiğin hiçbir dalı yoktur ki, ne kadar soyut olursa olsun, bir gün gerçek dünyada uygulama alanı bulmasın.
LOBACHEVSKY
Matematikte bir şeyleri asla anlamazsın, sadece onlara alışırsın.
John von Neumann
Eksi çarpı eksi artı edecek, Böyle yazılacak, böyle bilinecek, Kimse "neden?" demeyecek.
Anonim & Avni
Matematik ne neden söz ettiğimizi, ne de söyledğimiz şeyin doğru olup olmadığını bilmediğimiz bir konudur.
Bertrand Russell
Bir teoremin zerafeti onda görebildiğin fikirlerin sayısıyla doğru, o fikirleri görebilmek için harcadığın çabayla ters orantılıdır.
George Polya
Matematikçinin desenleri ressam veya şairlerinki gibi güzel olmalı, fikirleri renkler veya kelimeler gibi birbirlerine ahenkle uymalıdır. ... Dünyada çirkin matematik için asla daimi bir yer yoktur.
G. H. Hardy
Matematik gerekli sonuçları (conclusions) çıkaran bir bilimdir.
Benjamin Pierce
Mathemata mathematicis scribuntur. [Matematik matematikçiler için yazılır.]
Nicolaus Copernicus (1473-1543)
Matematikçiler aşıklar gibidir. Onlardan birine en küçük bir ilkeyi verin, o ondan bir sonuç (consequence) çıkaracaktır, tabi bu sonucu kabul etmeniz gerekecektir, o da bu sonuçtan başka bir sonuç çıkaracaktır.
Bernard le Bovier Fontenelle (1657-1757)
Geometri zekayı aydınlatır ve aklı doğru yola sokar. Onun bütün kanıtları açık ve düzenlidir. Çok iyi düzenlendiğinden geometrik mantık yürütmeye hata girmesi neredeyse imkansızdır. Bu nedenle sürekli geometriye başvuran bir aklın hataya düşmesi çok nadirdir. Buna göre de geometri bilen kişi zeka kazanır. Eflatun'un kapısında aşağıdaki sözlerin yazılı olduğu nakledilir: "Geometrici olmayan evimize giremez."
Ibn Haldun (1332-1406)
Matematikte büyük olmanın iki yolu vardır: İlki herkesten zeki olmak, ikincisi de herkesten aptal, fakat sebatlı olmak.
Raoul Bott
Bir karenin kenarlarıyla köşegenlerinin rasyonel orantılı olmadığı gerçeğinden habersiz olan, insan sıfatına layık değildir.
Plato (429-347 B.C.)
Matematikte bir şeyleri asla anlamazsın, sadece onlara alışırsın.
John von Neumann
Matematik ne neden söz ettiğimizi, ne de söyledğimiz şeyin doğru olup olmadığını bilmediğimiz bir konudur.
Bertrand Russell
Bir teoremin zerafeti onda görebildiğin fikirlerin sayısıyla doğru, o fikirleri görebilmek için harcadığın çabayla ters orantılıdır.
George Polya
Matematikçinin desenleri ressam veya şairlerinki gibi güzel olmalı, fikirleri renkler veya kelimeler gibi birbirlerine ahenkle uymalıdır. ... Dünyada çirkin matematik için asla daimi bir yer yoktur.
G. H. Hardy
Matematik gerekli sonuçları (conclusions) çıkaran bir bilimdir.
Benjamin Pierce
Matematikçiler aşıklar gibidir. Onlardan birine en küçük bir ilkeyi verin, o ondan bir sonuç (consequence) çıkaracaktır, tabi bu sonucu kabul etmeniz gerekecektir, o da bu sonuçtan başka bir sonuç çıkaracaktır.
Bernard le Bovier Fontenelle (1657-1757)
Geometri zekayı aydınlatır ve aklı doğru yola sokar. Onun bütün kanıtları açık ve düzenlidir. Çok iyi düzenlendiğinden geometrik mantık yürütmeye hata girmesi neredeyse imkansızdır. Bu nedenle sürekli geometriye başvuran bir aklın hataya düşmesi çok nadirdir. Buna göre de geometri bilen kişi zeka kazanır. Eflatun'un kapısında aşağıdaki sözlerin yazılı olduğu nakledilir: "Geometrici olmayan evimize giremez."
Ibn Haldun (1332-1406)
Transandantal sayıların gerçek veya kompleks sayılar alanındaki yeri böceklerin hayvanlar alemindeki yerine çok benzer. Herkes onların en kalabalık sınıf olduğunu bilir ancak çok az insan onların bir ya da ikisinden fazlasını ismen tanır.
Donald R. Newman
Matematik en bariz olanı en az bariz olan yolla kanıtlama işidir.
George Polya
(Sanki biraz haksızlık yapıyor, ama adam büyük bir matematikçi, ondan daha iyi bilecek değilim.)
Mantıksal olarak düşünülebilecek olanı mantıksal olarak düşünmek - matematikçinin amacı budur.
C. J. Keyser
Matematikteki en büyük ilerlemelerin bazıları daha sonra açıklanması zorunlu hale gelen küçük sembollerin icadıyla olmuştur; eksi işaretinden bütün negatif niceliklerin teorisi çıkmıştır.
Aldous Huxley
Hilbert'in bir matematik öğrencisi derslere devam etmemeye başlamıştı. Ona delikanlının şair olmak için ayrıldığını söylediler. Hilbert'in şöyle dediği nakledilir: "Ben zaten onun bir matematikçi olmasına yetecek kadar hayal gücüne sahip olduğunu hiç düşünmemiştim."
George Polya
Yeterli matematik çalışıncaya ve sayısız olası istisnaları görüp kafası karışıncaya kadar herkes bir eğrinin ne olduğunu bilir.
Felix Klein
Matematik zeka oyunları,Matematik eğlenceli oyunlar, bulmaca, satranç, sudoku,amiral battı oyna
 | |||
 |  | ||
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  | ||
kez okundu.
6.sınıf,7.sınıf,8.sınıf,1.dönem,2.dönem,matematik yazılı,sınav,soruları ,indir
Kastamonu Matematik | www.kastamonumatematik.com
Kastamonu Matematik | www.kastamonumatematik.com
EŞİTSİZLİKLER (video)
İçinde sayılar ve < , ≤ , > , ≥ sembollerinden birini içeren cebirsel ifadelere eşitsizlik denir.
Özellikleri:
Eşitsizliği çözmek,değişkenin eşitsizliği bozmayan değerlerini bulmak demektir.Eşitlik çözümünde, denklemi sağlayan bir tane değer bulunurken eşitsizlik çözümünde birden fazla değer bulunur.
Eşitsizliklerin Grafikleri ve Çizimleri
ax+by+c > 0
ax+by+c < 0
ax+by+c ≥ 0
ax+by+c ≤ 0
Yukarıda verilen eşitsizlikler birinci dereceden iki bilinmeyenli eşitsizliklerdir.Grafiği çizmeden önce eşittir kabul ederek denklemin x ve y sıralı ikili değerlerini buluruz.Bu sıralı ikililerden hareketle doğru grafiğimizi çizeriz.Daha sonra koordinat düzleminde bu doğru grafiğinin her hangi bir tarafında bir nokta yani sıralı ikili alınır.Bu nokta eşitsizliği sağlarsa grafik bu noktanın olduğu tarafa doğru taranır,sağlamazsa grafik diğer tarafa taranır.
ax+by+c ≥ 0
ax+by+c ≤ 0
Yukarıdaki eşittirli olanlar düz çizgili grafiktir.
ax+by+c > 0
ax+by+c < 0
Yukarıdaki eşittirli olmayanlar kesik çizgili grafiktir.
----------------------------------------------------

Doğrusal denklem sistemleri (Video)
İçerisinde eşitlik ve bir bilinmeyen bulunan rasyonel ifadelere bir bilinmeyenli rasyonel denklemler denir. [(2x+6)/(2x)]=8 Buradaki bilinmeyen yerine değişken de kullanılabilir.Denklemi doğru yapan değişkenin veya bilinmeyenin değerine denklemin çözümü, bu doğru değeri bulma işlemine denklemi çözme denir.Diğer bir deyişle denklemi sağlayan bilinmeyene denklemin kökü,denklemin köklerinden oluşan kümeye denklemin çözüm kümesi denir.
İki Değişkenli Denklemler
İçerisinde eşitlik ve iki değişken bulunan ifadelere iki değişkenli denklemler denir. (x+3y=9) İki değişkenli denklemin çözüm kümesi (x,y) ikililerinden oluşur.Bu denklem dik koordinat sisteminde doğru belirtir ve bu doğru üzerinde sonsuz sayıda nokta vardır.Bundan dolayı birinci dereceden iki değişkenli denklemlerin çözüm kümesi sonsuz elemanlıdır.
Aynı değişkenleri içeren iki doğrusal denklem doğrusal denklem sistemini oluşturur.Doğrusal denklem sistemlerinin çözümünde, yerine koyma yöntemi veya yok etme yöntemi kullanılır.Sistemin çözümü olan sıralı ikili her iki denklemi sağlamalıdır.
Denklem Sistemlerinin Çözüm Yöntemleri
Yerine Koyma Yöntemi
Verilen iki denklemin, herhangi birinden bilinmeyenlerden biri, diğeri cinsinden bulunur ve diğer denklemde yerine yazılır.Elde edilen bir bilinmeyenli denklem çözülür.Bulunan bu değer, denklemlerden herhangi birinde yerine yazılarak diğer bilinmeyen bulunur.
Yok Etme Yöntemi
Verilen her iki denklemin, bilinmeyenlerinden birinin katsayıları simetrik (mutlak değerce eşit ve zıt işaretli) olmalıdır.Bu koşul yoksa bilinmeyenlerden herhangi birinin, her iki denklemde de katsayıları simetrik duruma getirilir.Sonra her iki denklem taraf tarafa toplanarak bilinmeyenlerden biri yok edilir.Elde edilen br bilinmeyenli denklem çözülerek, bilinmeyenlerden biri bulunur.Bulunan bu değer, denklemlerden herhangi birinde yerine yazılarak diğer bilinmeyen bulunur.
Sayı örüntüleri (video)
Örüntü; belirli bir kuralla diziliş anlamına gelir.Bu diziliş bir sayı veya şekil dizilişi olabilir.
Önemli olan şey belirli bir kural ile ilerlemesidir.

Bu konuya girmeden önce, önemli bir örüntünün sahibi olan İtalya doğumlu Leonardo Fibonacci’den bahsetmek gerekir.Fibonacci 13. yüzyılda yaşamıştır.
Leonardi Fibonacci 1 1 2 3 5 8 13 21 …. şeklinde giden bir diziliş bulmuştur. Bu dizilişe Fibonacci sayı dizilişi adı verilir.
fibonacci sayı dizisinin terimleri nasıl elde edilir ?
Bu dizilişin kuralı şudur: 1. ve 2. sayı toplandığında 3. sayı elde edilir.
2. ve 3. sayı toplandığında 4. sayı elde edilir.
4. ve 5. sayı toplandığında 6. sayı elde edilir ve bu şekilde devam eder gider.
Bu önemli bir diziliştir ve doğada bile karşımıza çıkar. Zaten bu yüzden Fibonacci sayı dizisi önem kazanmıştır.
Örneğin çam kozalaklarının en uçtan arkaya doğru dizilişi bu şekildedir.
Bir kozalak bulun ve toplamlara bir gözatın.
Fibonacci sayıları PASCAL ÜÇGENİ’^nde de karşımıza çıkar.
Blaise PASCAL M.S 13. yüzyılda yaşamış fransız bir Matematikçidir ve kendi Soyadı ile anılan sayı dizisi vardır.
Daha doğrusu buna üçgen demek daha doğru olur.
PASCAL, üçgen ile sayılar arasındaki ilişkiyi tam 1653 sayfalık bir kitapta toplamıştır.
PASCAL, üçgeni oluştururken şunları yapmıştır.
1) En üste 1 yazmış.
2) Bir altına da 2 tane 1 yazmış.
3) Bundan sonra ise üstteki sayıları toplayıp bir aşağı yazmıştır. ( Yine en başa ve en sona 1 sayısını koymuştur. )
4) Şekle baktığımızda ise bir üçgen şekli oluşmuştur.
PASCAL üçgeninin ne işe yaradığını ise ileride Özdeşlikler konusunda göreceğiz.
Yukarıda anlattığımız PASCAL üçgeni için aşağıdaki şekli inceleyin.
Aritmetik geometrik diziler çalışma kağıdı test özel sayı örüntüleri çalışma kağıdı 8.sınıf matematik aritmetik diziler,geometrik diziler,fibonacci,pascal sayı örüntüleri ortak fark ortak çarpan indir.
Aritmetik geometrik diziler Çalışma kağıdını indirmek için yukarıdaki link'e tıklayın.
Kareköklü sayılarda çarpma işlemi (video)
Toplama ve çıkarma işleminde köklerin içindeki sayıların aynı olması gerekmekteydi.
Eğer aynı değilse kök içindeki fazlalıkları dışarı atarak, kök içlerini aynı yapmaya çalışıyorduk.
Kareköklü sayılardaki çarpma işleminde ise kök içlerinin aynı olma gibi bir şartı yok.
Tıpkı Rasyonel sayılardaki dört işlem gibi düşünelim bunu !
Rasyonel sayılarda toplama ve çıkarma işlemi yaparken paydalar eşitlenirdi fakat çarpma ve bölme işleminde eşitleme şart değildi.
Rasyonel sayılarda; pay ile pay, payda ile payda çarpılmaktaydı.
isterseniz bunları aşağıdaki örneklerle daha net açıklamaya çalışayım sizlere.

1) Çarpma işleminin 1. örneğinde 2 ve 4 katsayı olduğu için birbiriyle çarpıldı. Kök içindeki sayılar da birbiriyle çarpıldı. sonuçlar bulunduktan sonra, katsayılar yine katsayı kısmına, kök içleri de yine kök içine yazıldı.
2) Çarpma işleminin 2. örneğinde karşımıza çok çıkan bir örneği göstermek lazım. bir köklü sayıyı kendisiyle çarparsanız sonuçta o sayı kökten kurtulur. yani kök 3 x kök 3 = 3 olarak bulunur.
3) 3. örnekte ise yine 2 kareköklü sayı çarpılıyor. Katsayılar birbiriyle, kök içleri birbiriyle çarpıldı sonuç 14 kök 12 olarak bulundu fakat sonucumuz hala tam bulunmuş değil. Çünkü kök içindeki sayıyı parçalayarak bir kısmını dışarı çıkartabiliriz.
Nasıl dışarı çıkartıldığını anlayamadıysanız bir sonraki örnekte olduğu gibi; “bir sayıyı a kök b şeklinde yazma” yı inceleyin. Kareköklü sayıları a kök b şeklinde yazmak ne demektir ? Bazı kök içindeki sayılar öyle çarpanlarına ayrılır ki bir kısmı dışarı çıkabilir.
Yukarıdaki örneklerin 2. kısmında bulunan bir sayıyı a kök b şeklinde yazma kısmını inceleyelim.
1) 1. örnekte olduğu gibi kök 8 i 4.2 şeklinde yazarsak 4 dışarıya 2 olarak çıkar, fakat diğer 2 içeride kalır.
2) 2. örnekte olduğu gibi 48 sayısını 16.3 olarak yazabiliriz.16 sayısı kök dışına 4 olarak çıkar fakat 3 sayısı içeride kalır.
3) 3. örnekte de bir benzeri mevcut. (Yukarıdaki çarpma işleminin 3. sorusunda da bu işlemi yapmıştık )
NOT: Sayıları rastgele çarpanlarına ayıramayız. öyle bir çarpanlarına ayırmalıyız ki bunlardan biri kök dışına çıkabilsin.
Kareköklü sayılarda bölme işlemi
Kareköklü sayılarda çarpma işlemini gördük, bölme işleminin çok fazla farkı yok.
Çarpma işlemiyle aynı mantıkla işler.
Bölme işlemi yaparken;
Katsayılar ( kök dışındaki sayılar ) birbirine bölünür, kök içindeki sayılar da birbirine bölünür.
Bulunan sonuçlar ise uygun yere yazılır. Yani; katsayılar katsayı kısmına, kök içi de kök içindeki kısma yazılır.
Kareköklü sayılarda çarpma ve bölme işleminde aynı kök içindeki sayıları birbirinden ayırabiliriz, tam tersi olarak ayrı köktekileri aynı kök içine de alabiliriz.
isterseniz aşağıda yapılmış olan bölme işlemini inceleyelim.

1) Bu örneğimizde 8 ile 2 katsayı, 6 ile 3 kök içindeki sayılardır. Katsayıları birbirine, kök içlerini de birbirine böldük. Bulduğumuz sonuçlar 8/2=4 ve 6/3=2 yi uygun yerlerine yazdık.
2) Bu örnekte ise kök içindeki sayılar birbirine bölünemediği ve sadeleşemediği için kökleri birbirinden ayırdık.Ayrı ayrı kök dışına çıkardık.Sonucu 5/8 olarak bulduk
3) Bu örneğimizde bize bir ondalık sayı verildi ve ondalık sayımızı önce kesirli olarak yazdık.Sonrasında ise ayrı kök içinde yazdık.Daha sonrasında kök dışına çıkararak sonucu 7/10 oalrak bulduk.
4) Bu örneğimizde öncekinin tersini yaparak, ayrı kök içindeki sayıları tek kök içine aldık, sadeleştirme işlemini uygulayarak sayımızı kök 1/4 olarak bulduk. Sonrasında ise kökümüzü tekrardan birbirinden ayırdık, kök dışına çıkardık ve sonucu 1/2 olarak bulduk.

kareköklü sayılarla toplama çıkarma (video)
Kareköklü sayılarda toplama ve çıkarma işlemi yaparken kök içileri çok önemlidir.
Sadece kök içleri aynı olan sayılar birbirleriyle toplanır veya çıkartılabilir.
Kural ise aynı kesirlerin toplama ve çıkarma işlemine benzer.
Nasıl ki kesirler toplaıp çıkartılırken paydalar eşitlenip sabit kalıyorsa, köklü sayılarda da kök içleri aynı olursa işlem yapılabilir. Sonuç bulunurken kök içleri değişmez.
Aşağıdaki örnekleri inceleyelim.
Kök içi 2 olanları bir işlem yapıyoruz. Kök içi 7 olanları bir işlem yapıyoruz.
ikinci örneğin ikinci adımında zaten işlemimiz bitiyor. Daha fazla devam edemiyoruz.
Toplama ve çıkarma işlemini beraber anlatma nedenimiz işlem özelliklerinin aynı olması.
Kök içleri aynı olduktan sonra, kök dışındaki sayılarla tam sayılarda olduğu gibi 4 işlem yapılır.
işaretler aynı ise toplanır, büyük sayının işareti yazılır.
Kareköklü sayılarda diğer işlemleri ise sonraki konularda anlatacağız
 Karekök Bünyamin HOCA KONU ANLATIMI ve SORULARI VİDEOSU
Karekök Bünyamin HOCA KONU ANLATIMI ve SORULARI VİDEOSU
Çekilen kâğıtta ünlü harf olma olasılığı nedir?
Deney: Eş özelliklere sahip kâğıt üzerine yazılmış olan alfabemizdeki harflerden birinin seçilmesi.
Örnek uzay:
O={alfabemizdeki tüm harfler} veya
Ö={a,b,c,ç,d,e,f,g,ğ,h,ı,i,j,k,l,m,n,o,ö,p,r,s,ş,t,u,ü,v,y,z}, s(Ö)=29
Olay:
H={bir ünlünün çekilmesi}veya H={a,e,ı,i,o,ö,u,ü},
s(H)=8
Olayın çıktıları:
a, e, ı, i, o, ö, u, ü
Eş olasılıklı olma: Her bir harfin çekilme olasılığı eşittir.
Evrensel kümede her bir eleman bir kez yazılır fakat örnek uzayda çıktılar kaç tane ise o kadar yazılır.
Örnek:
a. “MATEMATİK” kelimesinin harflerinden oluşan evrensel küme: E={M, A, T, E, İ, K}
b. “Matematik” kelimesinin her bir harfi aynı özelliklere sahip kâğıt parçalarına yazılarak torbaya atılmıştır.
“Bakmadan bir kâğıt çekildiğinde çıkan harfin “A” olma olasılığı nedir?” sorusundaki örnek uzay:
Ö={M, A, T, E, M, A, T, İ, K}
OLASILIK ÇEŞİTLERİ NELERDİR?
Deneysel olasılık: Bir olasılık deneyi sonunda hesaplanan olasılığa denir. Bu olasılıkta deneyin yapıldığı problemin içinde geçer, problemi okuduğunuzda bir şeyler yapıldığını anlar, verileri görürsünüz.
örnek: Hileli bir zar 20 kez atıldığında 3 kez 1, 2 kez 2, 3 kez 3, 2 kez 4, 3 kez 5 ve 7 kez 6 geliyor. Buna göre bu zar atıldığında 5 gelme olasılığı kaçtır? cevap: 3/20
Teorik olasılık: Bir olasılık deneyinden teorik olarak beklenen olasılığa denir.Genelde şimdiye kadar karşılaştığımız problem tipleridir.İstenen durumların sayısını tespit edip tüm durumlara böleriz.
örnek: Bir zar atıldığında 3 gelme olasılığı kaçtır? cevap: 1/6
Öznel olasılık: Kişilerin kendi düşüncelerine göre karar verdikleri olasılıklara denir.Bu tip problemlerde kişilerin ismi ve tahmini yer alır.
örnek: 25 yumurtadan bazıları çift sarılıdır.Ali'ye göre alınacak bir yumurtanın çift sarılı olma olasılığı 10/25=0,4'tür. Ayşe'ye göre alınacak bir yumurtanın çift sarılı olma olasılığı 15/25=0,6'dır.
Üslü sayılar konu anlatımı içeriği; Üslü sayıların gösterimi, Negatif üslü sayılar, Üslü sayılar ve Özellikleri, Üssün üssü, Tek Veya Çift Kuvvetler, Çok Büyük Ve Çok Küçük Sayılar, Üslü sayılarda toplama ve çıkarma işlemi, Üslü sayılarda çarpma, Üslü sayılarda bölme işlemi, Üslü sayılar ile ilgili örnek sorular içermektedir.

Üslü sayılar yandaki şekilde de gösterildiği üzere; n tane a sayısının çarpımı anile ifade edilir. Bu ifadeye üslü sayı denir. Örnekler:
32 = 3 . 3 = 9
53 = 5 . 5 . 5 = 125
(- 2) 3 = (- 2) . (- 2) . (- 2) = - 8
Negatif Üs
Bir tam sayının üssü negatif ise bu sayı rasyonel olarak ifade edilir.
Örnek: 2 -3 = 1 / 8
Rasyonel bir sayının üssü negatif ise verilen rasyonel sayı ters çevrilir.
Örnek: (2 / 3) -3 = (3 / 2) 3 = 27 / 8
Üslü sayılarda negatif üssün görevi tabandaki sayıyı ters çevirmektir. Tabandaki sayının işaretini etkilemez.
ÜSLÜ SAYILARIN ÖZELLİKLERİ
Sıfır hariç her rasyonel sayının sıfırıncı kuvveti, daima (+1)' dir. Aşağıdaki örnekleri inceleyiniz.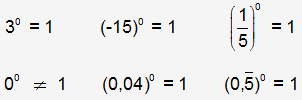
Her sayının birinci kuvveti yine kendisine eşittir. Örnekler:
91 = 9
(-0,5)1 = -0,5
(5/7)1 = 5/7
Rasyonel sayıların üslü sayı olarak yazılması;
Tam sayılı kesirler bileşik kesre çevrilir. Payın kuvveti alınarak paya yazılır. Paydanın kuvveti alınarak paydaya yazılır.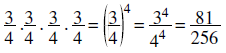
Ondalık kesirlerin üslü olarak yazılması;
(-0,5) . (-0,5). (-0,5) = ( -0,5)3 = -0,125
ÜSSÜN ÜSSÜ
Üslü bir sayının tekrar üssü alınırken; Taban aynen yazılır. Üsler çarpılarak tabana üs olarak yazılır. Üsleri çarpanken işaretlere dikkat ederek çarpınız. Aşağıdaki örnekleri inceleyiniz.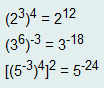
TEK VEYA ÇİFT KUVVETLER
Pozitif sayıların tüm kuvvetleri pozitiftir. Örnek: +24 = 16
Negatif sayıların tek kuvvetleri negatiftir. Örnek: (-3) 3 = -27
Negatif sayıların çift kuvvetleri ise pozitiftir. Örnek: (-3) 4 = +81
(-1)' in çift kuvvetleri (+1) , tek kuvvetleri ise (-1) dir.
ÇOK BÜYÜK VE ÇOK KÜÇÜK SAYILAR
Gezegenlerin Güneş'e olan uzaklıkları, Dünya'nın kütlesi gibi bilgileri öğrenirken bunların çok büyük sayılar ile ifade edildiğini görürüz. "a" gerçek sayı, 1 ≤ a < 10 ve n pozitif tam sayı olmak üzere a x 10n gösterimi, çok büyük sayıların bilimsel gösterimidir. Örneğin; 54 000 000 000 000 sayısının bilimsel gösterimi 5,4 x 1013 şeklindedir.
Maddeyi oluşturan taneciklerin kütleleri, bir virüsün uzunluğu gibi bilgiler çok küçük sayılar ile ifade edilirler. "a" gerçek sayı, 1 ≤ a < 10 ve n pozitif tam sayı olmak üzere a x 10-n gösterimi, çok küçük sayıların bilimsel gösterimidir. Örneğin; 0,000000032 sayısının bilimsel gösterimi 3,2 x 10-8 şeklindedir.
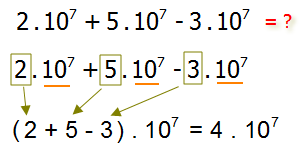
Tabanları ve üsleri aynı olan üslü sayılara benzer üslü sayılar denir. Üslü sayılar toplanırken veya çıkarılırken; Benzer üslü sayıların katsayıları toplanır veya çıkarılır. Bulunan sonucun yanına benzer üslü sayı yazılır. Soldaki örneği inceleyiniz. Örneğimizde altı turuncu çizili 10 üssü 7 ifadesi benzer üslü sayıdır. Bu ifadenin baş katsayıları toplanıp çıkarılarak sonuca yazılmıştır.
Benzer üslü sayı ise çarpım olarak yanına yazılmıştır. Üslü sayılarda toplama ve çıkarma işleminde kural aynıdır. Benzer üslü sayılar toplanıp çıkarılabilir. Bu işlem ise benzer üslü çoklukların baş katsayıları ile yapılır. Benzer üslü ifade aynen sonuca yazılır.
Üslü sayılarda çarpma işlemi yaparken, çarpılan üslü sayıların tabanları aynı üsleri farklı ise; ortak taban, taban olarak yazılır. Üsler toplanarak ortak tabana üs olarak yazılır. 1, 2 ve 3. örnekleri inceleyiniz.
Tabanları farklı, üsleri aynı olan üslü sayılar çarpılırken; Tabanlar çarpılıp taban olarak yazılır, ortak üs tabana üs olarak yazılır (Örnek 4). Tabanları ve üsleri farklı olan üslü sayılar çarpılırken; önce sayıların kuvvetleri alınır. Sonra çarpma işlemi yapılır (Örnek 5).
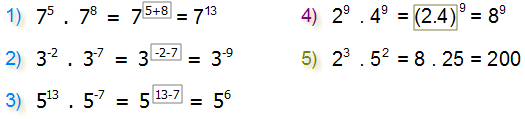

Üslü sayılarda bölme işlemi yaparken, üslü sayıların tabanları aynı üsleri farklı ise; ortak taban, taban olarak yazılır. Üsler çıkarılarak ortak tabana üs olarak yazılır. 1, 2 ve 3. örnekleri inceleyiniz. Üç farklı örnekle göstermemin sebebi; yapılan işaret hatalarını engellemek içindir. Negatif üslere çok dikkat ediniz.
Tabanları farklı, üsleri aynı olan üslü sayılar bölünürken; Tabanlar bölünüp taban olarak yazılır, ortak üs tabana üs olarak yazılır. 4. örneği inceleyiniz.
Tabanları ve üsleri farklı olan üslü sayılarda bölme işlemi yapılırken; ilk önce verilen üslü sayıların kuvvetleri alınır. Daha sonra bu sayılar arasında bölme işlemi yapılır. Örnek 5'i inceleyiniz.
Üslü sayılar ünitesini tamamladığınızda; Bir tam sayının negatif kuvvetini belirleyebilecek ve rasyonel sayı olarak ifade edebilecek, ondalık kesirlerin veya rasyonel sayıların kendileriyle tekrarlı çarpımını üslü sayı olarak yazabilecek ve değerini belirleyebilecek, üslü sayılarla toplama, çıkarma, çarpma ve bölme işlemlerini yapabilecek, çok büyük ve çok küçük pozitif sayıları bilimsel gösterimle ifade edebileceksiniz.
 .
.
Fraktallar Konu Anlatımı
Parçalanmış ya da kırılmış anlamına gelen Lâtince fractuuss kelimesinden gelmiştir. İlk olarak 1975'de Polonya asıllı matematikçi Benoit Mandelbrot tarafından ortaya atıldığı varsayılır. Kendi kendini tekrar eden ama sonsuza kadar küçülen şekilleri, kendine benzer bir cisimde cismi oluşturan parçalar ya da bileşenler cismin bütününü inceler.
Bir şeklin belirli bir oranda büyütülerek ya da küçültülerek oluşturulan örüntüleridir.

Fraktal sorularını çözerken genellikle bir önceki adıma bakılır eğer bir önceki adım bir sonraki adımda varsa ve orantılı olarak küçülüp büyümüşse fraktaldır diyebiliriz.
Yani her örüntü bir fraktal değildir ama her fraktal bir örüntüdür.
İşlemsel sorularda ise adım sayısı ileistenilen veriler karşılaştırılır.
Kısaca bir örüntünün Fraktal olması için
1- Örüntünün Büyüyüp küçülmesi gerekir.
2- Bir önceki şekli içinde barındırması gerekir.
3- Belirli bir kurala göre ilerlemesi gerekir.

bu şekiller fraktal değildir ama bir örüntüdür.
Örüntüde bir sonraki şekli tahmin edebilmeniz yeterlidir. Birsonraki şekilde yine bir daire olacaktır.
Fraktal değildir çünkü şekil büyüp küçülmemiş.

Yukardaki şekilde fraktal değil bir örüntüdür.
Örüntüdür çünkü sonraki şeklin önceki şekle bakarak ne kadar büyüyeceğini tahmin edebiliriz.
Fraktal değildir çünkü bir önceki şekil bir sonrakinde yok. Şeklin büyüyüp küçülmesi fraktal olamsı için yeterli değildir.

Yukardaki şekil ise hem fraktal hemde örüntüdür.
Şekil büyümüş
Bir önceki şekil diğerinin içinde
Ve bir kurala sahip.







Matematiğin Tarihi Gelişimi
Ortaçağ
İslâm Dünyası'nda başta aritmetik olmak üzere, matematiğin geometri, cebir ve trigonometri gibi dallarına önemli katkılarda bulunan matematikçiler yetişmiştir. Ancak bu dönemde gerçekleşen gelişmelerden en önemlisi, geleneksel Ebced Rakamları'nın yerine Hintlilerden öğrenilen Hint Rakamları'nın kullanılmaya başlanmasıdır.
Konumsal Hint rakamları, 8. yüzyılda İslâm Dünyası'na girmiş ve hesaplama işlemini kolaylaştırdığı için matematik alanında büyük bir atılımın gerçekleştirilmesine neden olmuştur.
Daha önce Arap alfabesinin harflerinden oluşan harf rakam sistemi kullanılıyordu ve bu sistemde sayılar, sabit değerler alan harflerle gösteriliyordu. Örneğin için a harfi, 10 için y harfi ve 100 içinse k harfi kullanılıyordu ve dolayısıyla sistem konumsal değildi. Böyle bir rakam sistemi ile işlem yapmak son derece güçtü.
Erken tarihlerden itibaren ticaretle uğraşanların ve aritmetikçilerin kullanmaya başladıkları Hint Rakamları'nın üstünlüğü derhal farkedilmiş ve yaygın biçimde kabul görmüştü. Bu rakamlar daha sonra Batı'ya geçerek Roma Rakamları'nın yerini alacaktır.
Cebir bilimi İslâm Dünyası matematikçilerinin elinde bağımsız bir disiplin kimliği kazanmış ve özellikle Hârizmî, Ebu Kâmil, Kerecî ve Ömer el-Hayyâm gibi matematikçilerin yazmış oldukları yapıtlar, Batı'yı büyük ölçüde etkilemiştir.
İslâm Dünyası'nda büyük ilgi gören ve geliştirilen bilimlerden birisi olan astronomi alanındaki araştırmalara yardımcı olmak üzere trigonometri alanında da seçkin çalışmalar yapılmıştır. Bu konudaki en önemli katkı, açı hesaplarında kirişler yerine sinüs, kosinüs, tanjant ve kotanjant gibi trigonometrik fonksiyonların kullanılmış olmasıdır.
Yeniçağ
Bu dönem diğer alanlarda olduğu gibi matematik alanında da yeniden bir uyanışın gerçekleştiği ve özellikle trigonometri ve cebir alanlarında önemli çalışmaların yapıldığı bir dönemdir.
Trigonometri, Regiomontanus, daha sonra da Rhaeticus ve Bartholomaeus Pitiscus`un çabalarıyla ve cebir ise Scipione del Ferro, Nicola Tartaglia, Geronimo Cardano ve Lodovice Ferrari tarafından yeniden hayata döndürülmüştür.
Yapılan çalışmalar sonucunda geliştirilen işlem simgeleri, şu anda bizim kullandıklarımıza benzer denklemlerin ortaya çıkmasına olanak vermiş ve böylelikle, denklem kuramı biçimlenmeye başlamıştır.
Rönesans matematiği özellikle Raffaello Bombelli, François Viète ve Simon Stevin ile doruk noktasına ulaşmıştır. 1585 yılında, Stevin, aşağı yukarı Takîyüddîn ile aynı anda ondalık kesirleri kullanmıştır.
Bu dönemde çağdaş matematiğin temelleri atılmış ve Pierre de Fermat sayılar kuramını, Pascal olasılık kuramını, Leibniz ve Newton ise diferansiyel ve integral hesabı kurmuşlardır.
Yakınçağ
Bu dönemde Euler ve Lagrange, integral ve diferansiyel hesabına ilişkin 17. yüzyılda başlayan çalışmaları sürdürmüş ve bu çalışmaların gök mekaniğine uygulanması sonucunda fizik ve astronomi alanlarında büyük bir atılım gerçekleştirilmiştir. Mesela Lagrange, Üç Cisim Problemi'nin ilk özel çözümlerini vermiştir.
Bu dönemde matematiğe daha sağlam bir temel oluşturmaya yönelik felsefi ağırlıklı çalışmalar genişleyerek devam etmiştir. Russell, Poincaré, Hilbert ve Brouwer gibi matematikçiler, bu konudaki görüşleriyle katkıda bulunmuşlardır.
Russell, matematik ile mantığın özdeş olduğunu kanıtlamaya çalışmıştır. Matematiğin, sayı gibi kavramlarını, toplama ve çıkarma gibi işlemlerini, küme, değilleme, veya, ise gibi mantık terimleriyle ve matematiği ise "p ise q" biçimindeki önermeler kümesiyle tanımlamıştır.
Hilbert'e göre ise, matematik soyut nesneleri konu alan simgesel bir sistemdir; mantığa indirgenerek değil, simgesel aksiyomatik bir yapıya dönüştürülerek temellendirilmelidir.
Sezgici olan Brouwer de matematiğin temeline, kavramlara somut içerik sağlayan sezgiyi koyar; çünkü matematik bir teori olmaktan çok zihinsel bir faaliyettir. Poincaré'ye göre de matematiğin temelinde sezgi vardır ve matematik kavramlarının tanımlanmaya elverişli olması gerekir.
Yine bu dönemin en orijinal matematikçileri olarak Dedekind ve Cantor sayılabilir. Dedekind, erken tarihlerden itibaren irrasyonel sayılarla ilgilenmeye başlamış, rasyonel sayılar alanının sürekli reel sayılar biçimine genişletilebileceğini görmüştür. Cantor ise, bugünkü kümeler kuramının kurucusudur.
MATEMATİK TARİHİ
Matematik insanlık tarihinin en eski bilimlerinden biridir. Çok eskiden, Matematik sayıların ve şekillerin ilmi olarak tanımlanırdı. Matematik de, diğer bilim dalları gibi, geçen zaman içinde büyük bir gelişme gösterdi; artık onu bir kaç cümle ile tanımlamak mümkün değildir. Şimdi söyleyeceklerim, matematiği tanımlamaktan çok, onun çeşitli yönlerini vurgulayan sözler olacaktır. Matematik bir yönüyle, resim ve müzik gibi bir sanattır. Matematikçilerin büyük çoğunluğu onu bir sanat olarak icra ederler. Bu açıdan bakınca, yapılan bir işin, geliştirilen bir teorinin, matematik dışında şu ya da bu işe yaraması onları pek ilgilendirmez. Onlar için önemli olan, yapılan işin derinliği, kullanılan yöntemlerin yeniliği, estetik değeri ve matematiğin kendi içinde bir işe yaramasıdır. Matematik, başka bir yönüyle, bir dildir. Eğer bilimin gayesi evreni; evrende olan her şeyi anlamak, onlara hükmetmek ve yönlendirmek ise, bunun için tabiatın kitabını okuyabilmemiz gerekir. Tabiatın kitabı ise, Galile’nin çok atıf alan sözleri ile, matematik dilinde yazılmıştır; onun harfleri geometrinin şekilleridir. Bunları anlamak ve yorumlayabilmek için matematik dilini bilmemiz gerekir. Matematik, başka bir yönüyle de satranç gibi entelektüel bir oyundur.
Kimi matematikçiler de ona bir oyun gözüyle bakarlar. Matematik, kullanıcısı için ise sadece bir araçtır. Matematiğin ne olduğunu, onun içine girdikten sonra, bilgimiz ölçüsünde ve ilgimiz yönünde, anlar ve algılarız. Artık matematik her hangi bir insan hükmedebileceği boyutların çok çok ötesindedir. Bu nedenle, matematikle uğraşan bizlerin, matematikten anladığımız ve onu algıladığımızın, file dokunan körün, fili anladığı ve onu algıladığından daha fazla olduğunu hiç sanmıyorum. Matematik sözcüğü, ilk kez, M.Ö. 550 lerde, Pisagor okulu üyeleri tarafından kullanılmıştır. Yazılı literatüre girmesi, Platon’ la M.Ö. 380 lerde olmuştur. Kelime manası “öğrenilmesi gereken şey”, yani, bilgidir. Bu tarihlerden önceki yıllarda, matematik kelimesi yerine, yer ölçümü manasına gelen, geometri yada eski dillerde ona eşdeğer olan sözcükler kullanılıyordu.
Matematiğin nerede ve nasıl başladığı hakkında da kesin bir şey söylemek mümkün değildir. Dayanak olarak yorum gerektiren arkeolojik bulguları değilde, yorum gerektirmeyecek kadar açık yazılı belgeleri alırsak, matematiğin M.Ö. 3000 -2000 yılları arasında Mısır ve Mezopotamya’da başladığını söyleyebiliriz. Heredot’a ( M.Ö. 485-415) göre, matematik Mısır’da başlamıştır. Bildiğiniz gibi, Mısır topraklarının %97 si tarıma elverişli değildir; Mısır’a hayat veren, Nil deltasını oluşturan %3 lük kısımdır. Bu nedenle, bu topraklar son derece değerlidir. Oysa, her sene yaşanan Nil nehrinin neden olduğu taşkınlar sonuncunda, toprak sahiplerinin arazilerinin hudutları belirsizleşmektedir. Toprak sahipleri de sahip oldukları toprakla orantılı olarak vergi ödedikleri için, her taşkından sonra, devletin bu işlerle görevli “geometricileri” gelip, gerekli ölçümleri yapıp, toprak sahiplerine bir önceki yılda sahip oldukları toprak kadar toprak vermeleri gerekmektedir. Heredot geometrinin bu ölçüm ve hesapların sonucu olarak oluşmaya başladığını söylemektedir. Matematiğin doğuşu hakkında ikinci bir görüş de, Aristo (M.Ö. 384-322) tarafından ileri sürülen şu görüştür. Aristo’ ya göre de matematik Mısır’da doğmuştur. Ama Nil taşmalarının neden olduğu ölçme-hesaplama ihtiyacından değil, din adamlarının, rahiplerin can sıkıntısından doğmuştur. O tarihlerde, Mısır gibi ülkelerin tek entelektüel sınıfı rahip sınıfıdır. Bu sınıfın geçimi halk veya devlet tarafından sağlandığı için, entelektüel uğraşılara verecek çok zamanları olmaktadır. Kendilerini meşgul etmek için, başkalarının satranç, briç, go… gibi oyunları içat ettikleri gibi onlar da geometri ve aritmetiği, yani o zamanın matematiğini icat etmişlerdir. Bu her iki görüş de doğru olabilir; rahipler geometricilerin işini kolaylaştırmak istemiş, yada dağıtımın adil yapıldığını kontrol için, üçgen, yamuk gibi bazı geometrik şekillerdeki arazilerin alanlarının nasıl hesaplanacağını bulmuş ve bu şekilde geometrinin doğmasına neden olmuş da olabilirler.
Matematiğin yazılı tarihini beş döneme ayıracağız. İlk dönem Mısır ve Mezopotamya dönemi olacak; bu dönem M.Ö. 2000 li yıllarla M.Ö. 500 lü yıllar arasında kalan 1500-2000 yıllık bir zaman dilimini kapsayacak. İkinci dönem, M.Ö. 500-M.S. 500 yılları arasında kalan ve Yunan Matematiği dönemi olarak bilinen 1000 yıllık bir zaman dilimini kapsayacak. Üçüncü dönem, M.S. 500 lerden kalkülüsün başlangıcına kadar olan ve esasta Hind, İslam ve Rönesans dönemi Avrupa matematiğini kapsayacak olan 1200 yıllık bir zaman dilimini kapsayacak. Dördüncü dönem, 1700-1900 yılları arasında kalan, matematiğin altın çağı olarak bilinen, klasik matematik dönemini kapsayacak. 1900 lerin başından günümüze uzanan, ve modern matematik çağı olarak adlandırılan, içinde bulunduğumuz dönem de beşinci dönem olacak. Her dönemi ayrı -ayrı ele alıp, eldeki kaynaklar çerçevesinde, o dönemdeki matematiğin gelişimi, katkı yapan matematikçiler, matematiğin toplum hayatındaki yeri ve o dönem matematiğinin temel özellikler hakkında bilgi vermeye çalışacağım.
1-Mısır ve Mezopotamya Matematiği
İlk döneme Mısır matematiği ile başlayacağız. Eski Mısır matematiği ve genelde de Mısır tarihi ile ilgili yazılı belge- arkolojik eser kalıntılarını kastetmiyorum- yok denecek kadar azdır. Bunun temel iki nedeni vardır. Birincisi, eski Mısırlıların yazıyı papirüslere yazmaları; ikinci nedeni ise İskenderiye kütüphanelerin geçirdikleri 3 büyük yangın sonucunda, ki bu yangınların sonuncusu 641 de Mısırın Müslümanlar tarafından fethi sırasında olmuştur, yazılı belgelerin yok olmuş olmasıdır. Papirüs, Nil deltasında büyüyen, kırmızımtırak renkte, saz türü bir bitkinin, ortalama 15-25 metre uzunluğunda ve 30-50 santim genişliğinde olan yapraklarıdır. Bu yapraklar kesilip, birleştirilip, preslendikten ve bazı basit işlemlerden geçirildikten sonra, kağıt yerine yazı yazmak için kullanılırmış. “Paper” , “papier” gibi batı dillerindeki kağıt karşılığı sözcükler, papirüs sözcüğünden türetilmiştir. Bir papirüsün ortalama ömrü 300 yıldır; 300 yıl sonra, nem, ısı ve benzeri nedenlerle, pul-pul olup dökülmektedir. Günümüze, matematikle ilgili, istisnai şartlar altında saklandığı anlaşılan, iki papirüs gelmiştir. Mısır matematiği hakkındaki bilgimizin ana kaynakları bu iki papirüstür. Bu papirüslerden ilki, Ahmes ( ya da Rhind ) papirüsü olarak bilinen, 6 metre uzunluğunda ve 35 cm kadar genişliğinde olan bir papirüstür. Bu papirüsün, M.Ö. 2000 li yıllarda yazılmış olan bir pürüsün, M.Ö. 1650 lerde Ahmes isimli bir “matematikçi” tarafından yazılan bir kopyasıdır. Bu papirüsü 1850 lerde İrlandalı antikacı H. Rhind satın almış, şimdi British museum dadır. Bu papirüs, matematik öğretmek gayesiyle yazılmış bir kitaptır. Giriş kısmında, kesirli sayılarla işlemleri öğretmek gayesiyle verilen bir-kaç alıştırmadan sonra, çözümleriyle 87 soru verilmektedir. Bu sorular, paylaşım hesabı, faiz hesabı veya bazı geometrik şekillerin alanını bulmak gibi, insanların günlük hayatta karşılaşabileceği türden sorulardır. Bu az-çok bizim 8. sınıf matematiği düzeyinde bir matematiktir. Moskova papirüsü diye bilinen ve şimdi Moskova müzesinde olan ikinci papirüs de M.Ö. 1600 lerde yazılmış bir kitapçıktır. Bu papirüs 25 soru içermektedir. Bu sorular, ikisi hariç, Ahmes papirüsündeki sorular türündendir. Diğer iki soruya gelince, onlardan biri, bir düzlemle kesilen küre parçasının hacmi ve yüzeyinin alanının hesaplanmasıdır. Diğeri ise, yine bir düzlemle kesilen bir piramidin hacminin bulunması sorusudur. Her iki soru da doğru olarak çözülmüştür. Bu iki soru Mısır matematiğinin zirvesi olarak kabul edilmektedir. Mısırlılar, dairenin alanının çapına orantılı olduğunun farkına varmışlar ve pi sayısını 4x(8/9) un karesi, yani 256/81=3,16 olarak bulmuşlardır. Mısır matematiğini 2000 yıl boyunca bu düzeyde kaldığı ve kayda değer bir ilerleme göstermediği anlaşılmaktadır.
-. İlk döneme Mısır matematiği ile başlayacağız. Eski Mısır matematiği ve genelde de Mısır tarihi ile ilgili yazılı belge- arkolojik eser kalıntılarını kastetmiyorum- yok denecek kadar azdır. Bunun temel iki nedeni vardır. Birincisi, eski Mısırlıların yazıyı papirüslere yazmaları; ikinci nedeni ise İskenderiye kütüphanelerin geçirdikleri 3 büyük yangın sonucunda, ki bu yangınların sonuncusu 641 de Mısırın Müslümanlar tarafından fethi sırasında olmuştur, yazılı belgelerin yok olmuş olmasıdır. Papirüs, Nil deltasında büyüyen, kırmızımtırak renkte, saz türü bir bitkinin, ortalama 15-25 metre uzunluğunda ve 30-50 santim genişliğinde olan yapraklarıdır. Bu yapraklar kesilip, birleştirilip, preslendikten ve bazı basit işlemlerden geçirildikten sonra, kağıt yerine yazı yazmak için kullanılırmış. “Paper” , “papier” gibi batı dillerindeki kağıt karşılığı sözcükler, papirüs sözcüğünden türetilmiştir. Bir papirüsün ortalama ömrü 300 yıldır; 300 yıl sonra, nem, ısı ve benzeri nedenlerle, pul-pul olup dökülmektedir. Günümüze, matematikle ilgili, istisnai şartlar altında saklandığı anlaşılan, iki papirüs gelmiştir. Mısır matematiği hakkındaki bilgimizin ana kaynakları bu iki papirüstür. Bu papirüslerden ilki, Ahmes ( ya da Rhind ) papirüsü olarak bilinen, 6 metre uzunluğunda ve 35 cm kadar genişliğinde olan bir papirüstür. Bu papirüsün, M.Ö. 2000 li yıllarda yazılmış olan bir pürüsün, M.Ö. 1650 lerde Ahmes isimli bir “matematikçi” tarafından yazılan bir kopyasıdır. Bu papirüsü 1850 lerde İrlandalı antikacı H. Rhind satın almış, şimdi British museum dadır. Bu papirüs, matematik öğretmek gayesiyle yazılmış bir kitaptır. Giriş kısmında, kesirli sayılarla işlemleri öğretmek gayesiyle verilen bir-kaç alıştırmadan sonra, çözümleriyle 87 soru verilmektedir. Bu sorular, paylaşım hesabı, faiz hesabı veya bazı geometrik şekillerin alanını bulmak gibi, insanların günlük hayatta karşılaşabileceği türden sorulardır. Bu az-çok bizim 8. sınıf matematiği düzeyinde bir matematiktir. Moskova papirüsü diye bilinen ve şimdi Moskova müzesinde olan ikinci papirüs de M.Ö. 1600 lerde yazılmış bir kitapçıktır. Bu papirüs 25 soru içermektedir. Bu sorular, ikisi hariç, Ahmes papirüsündeki sorular türündendir. Diğer iki soruya gelince, onlardan biri, bir düzlemle kesilen küre parçasının hacmi ve yüzeyinin alanının hesaplanmasıdır. Diğeri ise, yine bir düzlemle kesilen bir piramidin hacminin bulunması sorusudur. Her iki soru da doğru olarak çözülmüştür. Bu iki soru Mısır matematiğinin zirvesi olarak kabul edilmektedir. Mısırlılar, dairenin alanının çapına orantılı olduğunun farkına varmışlar ve pi sayısını 4x(8/9) un karesi, yani 256/81=3,16 olarak bulmuşlardır. Mısır matematiğini 2000 yıl boyunca bu düzeyde kaldığı ve kayda değer bir ilerleme göstermediği anlaşılmaktadır.
Mısır sayı sistemi, on tabanına göredir ve rakam sistemlerinin yazımı ve kullanımı Romen rakamlarının yazım ve kullanımı gibidir. Bu rakamlarla hesap yapmanın çok zor olduğu, Romen rakamlarıyla hesap yapmayı deneyen herkesin kolayca göreceği gibi, açıktır. Mısır matematiğinin gelişmemesinin bir nedeni bu olabilir.
Mezopotamya’da yaşamış medeniyetlerden (Sümerler, Akatlar, Babiller, Kaldeyenler, Asurlar, Urlar, Huriler,…; fetihler nedeniyle, bir zaman Hititler, Persler,…) zamanımıza, Mısırdan kalandan bin kat daha fazla yazılı belge kalmıştır. Bunun nedeni, Mezopotamyalıların yazı aracı olarak kil tabletleri kullanmalarıdır. Pişirilen yada güneşte iyice kurutulan bir kil tabletin ömrü sonsuz denecek kadar uzundur. Yapılan kazılarda yarım milyondan fazla tablet bulunmuştur. Bu tabletlerin önemli bir kısmı İstanbul arkeoloji müzesindedir. Diğerleri de dünyanın çeşitli – Berlin, Moskova, British, Louvre, Yel, Colombia ve Pensilvanya- müzelerindedir. Bu tabletlerin, şimdiye kadar incelenmiş olanlarının içinde, beş yüz kadarında matematiğe rastlanmıştır. Bu bölgede yaşamış medeniyetlerin matematiği hakkında bilgimiz bu tabletlerden gelmektedir. Bu tabletlerden anlaşılan, Mezopotamya’da matematik, Mısır matematiğinden daha ileridir; Mezopotamyalılar lise iki düzeyinde bir matematik bilgisine sahiptirler. Mısırlıların bildikleri matematiği bildikleri gibi, ikinci dereceden bazı polinomların köklerini bulmasını, iki bilinmeyenli iki denklemden oluşan bir sistemi çözmesini de biliyorlar. Şunu söylemem gerekir ki, o zamanlarda henüz negatif ve irrasyonel sayılar bilinmemektedir. Bu nedenle ikinci dereceden her polinomun köklerini bulmaları mümkün değildir. Mezopotamyalılar, daha sonra Pisagor teoremi olarak adlandırılacak olan teoremi de biliyorlardı. Pi sayısını karesi 10 olan bir sayı olarak bilmekteler. Daha sonraları 3.15 olarak da kullanmışlardır.
Mezopotamyalıların sayı sistemi 60 tabanlı bir sayı sistemidir. Bu sayı sistemi günümüzde de, denizcilik ve astronomi de kullanılmaktadır. Bizim sayı sisteminde 10 ve 10 nun kuvvetlerini kullandığımız ve sayıları buna göre basamaklandırdığımız gibi, onlar da sayıları 60 ve 60 ın kuvvetlerine göre basamaklandırmaktadırlar. Bu sayı sisteminin en önemli özelliği basamaklı, yani konumlu, bir sayı sistemi olmasıdır. Saatin 60 dakika, günün 24 saat ve dairenin 360 dereceye bölünmüş olması bize bu sayı sisteminden kalan miraslardan sadece bir kaçıdır. Mezopotamyalıların 60 tabanlı bir sayı sistemi seçmiş olmalarının nedeni bilinmemektedir. Bu konuda ileri sürülen belli-başlı üç görüş ya da varsayım şunlardır: 1). 60 sayısının 2,3,4,5,6,10,12,20,30 gibi çok sayıda bölenleri olması onu günlük hayatta çok kullanışlı kılıyordu; bu nedenle 60 tabanlı bir sayı sistemi seçmişlerdir. 2). 60 tabanlı sayı sisteminin seçiminden önce, o bölgede 10 ve 12 tabanlı sayı sistemlerini kullanan medeniyetler olmuştur. Daha sonra gelen bir medeniyet, daha önceki ölçü birimleriyle uyum sağlamak için, 10 ile 12 nin en küçük ortak katı olan 60 ‘ı sayı sistemlerinin tabanı olarak almışlardır. 3). 60 tabanlı sayı sisteminin seçimi, bir eldeki, baş parmak hariç, dört parmakta bulunan üç eklem yerini o zamanın insanları sayı saymak için kullanıyorlardı; 4 parmakta 12 eklem yeri olduğu ve bir elde de beş parmak olduğu için bu iki sayının çarpımı olan 60 ‘ ı sayı sistemlerinin tabanı olarak almışlardır. Bu konuda görüşler bunlardır. Eğer bir gün 60 sayısının niçin seçildiğini izah eden bir tablet bulunursa o zaman gerçek anlaşılacaktır.
Bu dönemin matematiğini toptan değerlendirecek olursak, temel özellikleri şunlardır. a) Bu dönem matematiğinde teorem, formül ve ispat yoktur. Bulgular emprik veya deneysel; işlemler sayısaldır. Bunun böyle olması kaçınılmazdır zira o dönemde matematik, simgesel olarak değil, sözel olarak ifade edilmekte. Sözel ve sayısal matematikte ( geometrik çizimler hariç) formel ispat vermek olanaksız olmasa da, kolay değildir. b) Bu dönemin matematiği zanaat düzeyinde bir matematiktir; matematik “matematik için matematik “ anlayışıyla değil, günlük hayatın ihtiyaçları için, yani “halk için matematik “ anlayışıyla yapılmaktadır. Matematiğin kullanım alanları ise, zaman-takvim belirlemek, muhasebe işleri ve günlük hayatın, inşaat, miras dağıtımı gibi diğer işleridir. Dini ve milli günlerin, ibadet saatlerinin, deniz yolculuklarının ve tarıma uygun dönemlerin belirlenmesi için, bugün olduğu gibi, eski zamanlarda da doğru bir takvim yapmak son derece önemli bir iş olmuştur. Bu da ancak uzun süreli gözlem, ölçüm ve hesapla mümkündür. Bu matematiğin kullanım alanlarından en önemlisi ve matematiğin gelişmesine neden olan temel ihtiyaçlardan biridir. Devlet gelir-giderinin hesaplanması, mal varlıklarını tespit, kayıt ve muhasebesi de devlet düzeni için elzem olan ve matematiğin kullanıldığı diğer bir alandır. Buda matematiğin öğretilmesine ve dolaysıyla gelişmesine neden olan ikinci bir temel ihtiyactır.
Bu dönem matematiği, bu bölge ülkelerinin kültürel varlıklarının, Pers istilası sonucu son bulmasıyla son bulur.
2- Yunan Matematiği
M.Ö. 600 lü yıllar Pers’lerin orta doğuya hakim olmaya başladığı yıllardır. M.Ö. 550’ li yıllara gelindiğinde, Pers’ler, Anadolu, Mısır dahil, bütün orta doğunun tek hakimidirler. Pers’ler, M.Ö.500-480 arasında Yunanistan’a üç sefer düzenlerler; 480 de Atina’yı ele geçirerek yakarlar ama, bir yıl sonra, 479 da Yunanlılar Persleri Yunanistan’dan atarlar. Bu tarih, M.Ö. 479, Yunan medeniyetinin başlangıcı olarak kabul edilen tarihtir. Bu tarih, bilimde, sanatta edebiyatta çok parlak bir dönemin başlangıcı olan bir tarihtir. Yunan matematiği gerçekte bu dönemden daha önce başlamıştır. İki kişi, Tales (M.Ö. 624-547) ve Pisagor ( M.Ö.569-475), Yunan matematiğinin babası olarak kabul edilir. Tales Milet (Aydın) de doğmuştur. Mısır’a gittiği, bir süre orada kaldığı ve Mısırda geometri öğrendiği bilinmektedir. Mısırda iken, büyük piramidin gölgesinin uzunluğunu ölçerek, bu sayıyı, kendi boyunun o andaki gölgesinin boyuna olan oranıyla çarpmak suretiyle, büyük piramidin yüksekliğini hesapladığı kitaplarda anlatıla gelmektedir. Tales Milet’e döndükten sonra, öğrendiklerini öğretmek gayesiyle, kendi etrafında bir grup oluşturarak onlara geometri öğretmiştir. Matematiğe – deneysel olarak doğrulamaya dayanmayan-akıl yürütmeye dayalı, soyut ispatın Tales’le girdiği kabul edilir. Ayrıca, Tales insanlık tarihinin ilk filozofu olarakta kabul edilen kişidir. Yunan matematiğinin diğer babası olan Pisagor Samos (Sisam) adasında doğmuştur. Pisagor’un bir süre Tales’in yanında kaldığı, onun tavsiyelerine uyarak Mısır’a gittiği, orada geometri öğrendiği, Mısır tapınaklarını ziyaret edip, dini bilgiler edindiği, ve Mısırın Pers’ler tarafından işgali sırasında, Pers’lere esir düşerek Babil’e götürüldüğü bilinmektedir. Babil’de bulunduğu 5 yıl boyunca matematik, müzik ve dini bilgiler öğrenmiş, Samos’a döndükten sonra bir okul oluşturarak etrafına topladığı insanlara öğrendiklerini öğretmeye çalışmıştır. Siyasi nedenlerle, M.Ö. 518 Samos’dan ayrılarak, güney Italya’ya, Crotone şehrine yerleşmiş ve orada yarı mistik-yarı bilimsel, tarikat vari bir okul oluşturmuştur. Bu okulun, “matematikoi” denen üst düzey kişileri beraber yaşamaktalar ve birbirlerine yeminle bağlıdırlar. İkinci gurup okula devam eden öğrencilerden oluşmaktadır. Pisagor okulu sayı kültü üzerine kuruludur. Onlara göre, her şey sayılara indirgenebilir; sayılar arasında tesadüfi olamayacak kadar mükemmel bir harmoni vardır ve harmoni ilahi harmoninin yansımasıdır. O gün için bilinen sayılar 1,2,3,… gibi çokluk belirten tam sayılar; ve ½, ¾,…gibi parçanın bir bütüne oranını belirten kesirli sayılardır. Pisagor teoremi olarak bilinen ( bir dik üçgenin dik kenarlarının karesin toplamı hipotenüsün karesine eşittir) teorem ile irrasyonel sayıların ortaya çıkması Pisagor ekolünü derin bir krize sokmuştur. İrrasyonel sayıların keşfi matematiğin ilk önemli krizidir. Pisagor okulunun üyelerinin bir çoğu Cylon isimli bir yobazın yönettiği bir baskın sonuncu katledilmişlerdir. Pisagor hayatını kurtarmıştır ama bir kaç sene sonra o da ölmüştür. Pisagor’un düşünceleri, Pisagor ekolu, şu veya bu isim altında uzun yıllar yaşamıştır. Bu bilgilerden de anlaşılacağı gibi, Yunan matematiğinin temelinde Mısır ve Mezopotamya matematiği vardır.
- M.Ö. 600 lü yıllar Pers’lerin orta doğuya hakim olmaya başladığı yıllardır. M.Ö. 550’ li yıllara gelindiğinde, Pers’ler, Anadolu, Mısır dahil, bütün orta doğunun tek hakimidirler. Pers’ler, M.Ö.500-480 arasında Yunanistan’a üç sefer düzenlerler; 480 de Atina’yı ele geçirerek yakarlar ama, bir yıl sonra, 479 da Yunanlılar Persleri Yunanistan’dan atarlar. Bu tarih, M.Ö. 479, Yunan medeniyetinin başlangıcı olarak kabul edilen tarihtir. Bu tarih, bilimde, sanatta edebiyatta çok parlak bir dönemin başlangıcı olan bir tarihtir. Yunan matematiği gerçekte bu dönemden daha önce başlamıştır. İki kişi, Tales (M.Ö. 624-547) ve Pisagor ( M.Ö.569-475), Yunan matematiğinin babası olarak kabul edilir. Tales Milet (Aydın) de doğmuştur. Mısır’a gittiği, bir süre orada kaldığı ve Mısırda geometri öğrendiği bilinmektedir. Mısırda iken, büyük piramidin gölgesinin uzunluğunu ölçerek, bu sayıyı, kendi boyunun o andaki gölgesinin boyuna olan oranıyla çarpmak suretiyle, büyük piramidin yüksekliğini hesapladığı kitaplarda anlatıla gelmektedir. Tales Milet’e döndükten sonra, öğrendiklerini öğretmek gayesiyle, kendi etrafında bir grup oluşturarak onlara geometri öğretmiştir. Matematiğe – deneysel olarak doğrulamaya dayanmayan-akıl yürütmeye dayalı, soyut ispatın Tales’le girdiği kabul edilir. Ayrıca, Tales insanlık tarihinin ilk filozofu olarakta kabul edilen kişidir. Yunan matematiğinin diğer babası olan Pisagor Samos (Sisam) adasında doğmuştur. Pisagor’un bir süre Tales’in yanında kaldığı, onun tavsiyelerine uyarak Mısır’a gittiği, orada geometri öğrendiği, Mısır tapınaklarını ziyaret edip, dini bilgiler edindiği, ve Mısırın Pers’ler tarafından işgali sırasında, Pers’lere esir düşerek Babil’e götürüldüğü bilinmektedir. Babil’de bulunduğu 5 yıl boyunca matematik, müzik ve dini bilgiler öğrenmiş, Samos’a döndükten sonra bir okul oluşturarak etrafına topladığı insanlara öğrendiklerini öğretmeye çalışmıştır. Siyasi nedenlerle, M.Ö. 518 Samos’dan ayrılarak, güney Italya’ya, Crotone şehrine yerleşmiş ve orada yarı mistik-yarı bilimsel, tarikat vari bir okul oluşturmuştur. Bu okulun, “matematikoi” denen üst düzey kişileri beraber yaşamaktalar ve birbirlerine yeminle bağlıdırlar. İkinci gurup okula devam eden öğrencilerden oluşmaktadır. Pisagor okulu sayı kültü üzerine kuruludur. Onlara göre, her şey sayılara indirgenebilir; sayılar arasında tesadüfi olamayacak kadar mükemmel bir harmoni vardır ve harmoni ilahi harmoninin yansımasıdır. O gün için bilinen sayılar 1,2,3,… gibi çokluk belirten tam sayılar; ve ½, ¾,…gibi parçanın bir bütüne oranını belirten kesirli sayılardır. Pisagor teoremi olarak bilinen ( bir dik üçgenin dik kenarlarının karesin toplamı hipotenüsün karesine eşittir) teorem ile irrasyonel sayıların ortaya çıkması Pisagor ekolünü derin bir krize sokmuştur. İrrasyonel sayıların keşfi matematiğin ilk önemli krizidir. Pisagor okulunun üyelerinin bir çoğu Cylon isimli bir yobazın yönettiği bir baskın sonuncu katledilmişlerdir. Pisagor hayatını kurtarmıştır ama bir kaç sene sonra o da ölmüştür. Pisagor’un düşünceleri, Pisagor ekolu, şu veya bu isim altında uzun yıllar yaşamıştır. Bu bilgilerden de anlaşılacağı gibi, Yunan matematiğinin temelinde Mısır ve Mezopotamya matematiği vardır.
Şimdi Atina’ ya dönelim. Atina’ da matematiğin sistematik eğitimi Platon’la (M.Ö. 427-347) başlar. Sokrat’ın öğrencisi olan Platon, Sokrat’ın ölüme mahkum edilip, zehir içerek ölmesinden sonra, uzun bir yolculuğa çıkar; 10 yıl kadar Mısır, Sicilya ve Italya’da kalır. Orada, Pisagorculardan matematik öğrenir. Matematetiğin doğru düşünme yetisi için ne denli önemli olduğunu anlayan Platon, Atina’ya döndüğünde, M.Ö. 387 de, bir okul kurar ve ona Pers-Yunan savaşların kahramanlarından Akademius’un ismini verir. ( Bazı kaynaklara göre de Akademos, Platon’un okulunun kurulu olduğu alanın sahibinin ismidir). Bu Platon’un “akademi”sidir. Bu akademinin girişinde “her kim ki geometrici değildir, içeriye girmesin yazılıdır”. O tarihlerde, henüz matematik sözcüğü kullanılmaktadır, “geometri” matematik sözcüğünün yerine kullanılmıştır. Bu okulda felsefe, geometri, müzik ( harmoni teorisi) ve jimnastik ağırlıklı bir eğitim verilmektedir. Geometri doğru düşünmeyi öğrenmenin temel aracı olarak kabul edilmekte ve o tarihlerde felsefe ile geometri içice denecek kadar birbirine yakın konular olarak görülmektedir. Platon bir araştırma yöneticisi gibi görev yapmakta, öğrencilerine çeşitli geometri soruları vererek, onlardan bu soruları halletmelerini istemektedir. Bu okul M.S. 529’ a kadar, 900 yıldan fazla faaliyet gösterecektir. Bu okulda çok sayıda matematikçi yetişmiştir. Burada yetişen ilk önemli matematikçi Öklid (Euclid) ( M.Ö.325-265); son önemli matematikçi Proclus (M.S. 411-485) tur. Bu dönemin matematiği hakkında en önemli kaynak Proclus’un eserleridir. M.Ö.400-300 yıllarının en önemli matematikçi-bilim adamı, Platon’un akademisinde de hocalık da yapmış olan, Eudoxus’tur. Pisagorcuların sayı kavramını değiştirerek, sayı’yı iki uzunluğun oranı olarak tanımlayan ve bu tanıma uygun bir sayılar aritmetiği geliştirerek, irrasyonel sayıların keşfi sonucu, matematiği içine düşmüş olduğu krizden kurtaran; entegral kavramının temelinde olan “exhaustion” yöntemini geliştiren ve ilk olarak bir evren modeli tasarlayan Eudoxus’tur. “Exhaustion” yöntemi şekli düzgün olmayan, dolaysıyla alanı yada hacmi bilinmeyen bir cismin alan veya hacmini, alanı yada hacmi bilinen şekillerle doldurarak o alanı yada hacmi hesaplama yöntemidir.
M.Ö. 335 den itibaren, Mekodonya’lı büyük İskender, 12-13 yıl gibi kısa bir sürede Pers imparatorluğunun tamamını ele geçirir. Hindistan dönüşü, 322 de Babil’de ölür. İskender’in ölümünden sonra, İskender’in generalleri kanlı bir iktidar mücadelesine girişirler. Bu mücadele sonucu, İskender’in imparatorluğu üçe bölünür. İmparatorluğun Afrikadaki toprakları ( Mısır , Libya ) general Potelemi’ye, imparatorluğun Asya’daki toprakları general Seleukos’a ve Avrupa’daki topraklarda Antigonos’e düşer. Böylelikle, daha sonra “ Yunan kültür bölgeleri” diye adlandırılacak olan Yunan medeniyetinin gelişeceği üç bölge ortaya çıkar.
Bunlar Yunanistan-Mekadonya, Anadolu-Suriye ve Mısır-Libya dır. Makedonya krallığında Plato’un akademisi, Aristo’nun Lisesi gibi okullar eğitimlerini daha uzun yıllar sürdürürler ama daha çok felsefe ağırlıklı olarak. Anadolu’da tıp ve astronomide önemli bilginler yetişir, Galen ve Hipparkus gibi. Galen’nin tıp konusunda 500 civarında kitap (papirüs) yazdığı bilinmektedir. Galen, her ne kadar da Hipokrat ve İbni Sina kadar ismi bilinen bir kişi değilse de, tarihin en önemli tıp adamlarından biridir. Matematik açısından ise en önemli merkez İskenderiye’dir. Potelemi, Zeus’un sanat tanrıçaları olarak bilinen kızlarına verilen (Muse) isminden esinlenerek, İskenderiye’de tarihin en ünlü Üniversitelerinden birini, Museum’u kurar. Burası M.Ö. 312-M.S. 421 tarihler arasında, 700 yıldan fazla bir zaman diliminde bir ileri bilimler merkezi olarak eğitim ve araştırma faaliyetlerini sürdürecektir. Burası, ücretleri devlet hazinesinden ödenen, 100 den fazla bilim adamının çeşitli dallarda eğitim verdiği ve araştırma yaptığı bir kurumdur. Zamanla çok zengin bir kütüphane oluşturacaklar, botanik bahçesi ve bir gözlem evine sahip olacaklardır. Yunan kültür bölgelerine ait önemli bilim adamları burayı ziyaret edip, burada bir süre kalmışlardır. Burada ders veren ilk önemli matematikçi Öklid’ tir. Öklid’in yazdığı çok sayıda eser arasında en önemlisi, Öklid’in elementleri olarak bilinen 13 kitaplık bir dizi matematik kitaplarıdır. O tarihlerdeki kitap uzunlukları bir papirüslüktür.
Bu da bizim ölçülerimizle, 20 ile 50 sayfa arasında bir kitaba karşılık gelmektedir. Bu kitaplarda Öklid o zamanlarda bilinen matematiğinin sistematik bir derlemesini sunar. Bu eserin önemi Öklid’in geometriye yaklaşımımda ve konuların takdimindedir. Öklid, geometride, önce, evrensel geçerliği olan, 5 aksiyom verir. Bunlar A=B ve B=C ise A=C gibi her sağduyunun kabul edeceği kurallardır. Sonra nokta, doğru, düzlem gibi kavramların ne olduğunu belirten 31 tanım verir. Sonra da Öklid geometrisinin postulatları olarak bilinen şu beş postulatı verir. 1) iki noktadan bir doğru geçer. 2) bir doğru parçası sınırsız uzatılabilir. 3) bütün dik açılar bir birine eşittir. 4) Bir nokta ve bir uzunluk bir çember belirler. 5) Bir doğruya onun dışındaki bir noktadan sadece bir paralel çizilir. Daha sonra, gökten bir şeyler düşürmeden, mantıki çıkarım yoluyla, bu postulatlardan çıkarabildiği sonuçları teorem, önerme olarak mantıki bir sırada sunar.
Aksiyomatiko-dedüktif yaklaşım dediğimiz bu yaklaşım bugünkü matematiğin ve bilimin de temel yaklaşımıdır. Ünlü düşünür Bertrand Russell’a göre, hiç bir kitap batı düşünce sisteminin oluşmasında bu kitap kadar etkili olmamıştır. Bu kitap tarih boyunca belli-başlı bütün dillere çevrilmiş, 1000 defadan fazla basılmış, bütün medeniyetlerin okullarında okutulmuş, insanlığın en önemli baş yapıtlarından biridir. Museum da yetişen en önemli matematikçilerden biri de Perge’li Apollonius’tur. Antik Çağın, Öklid ve Arşimed’le beraber üç büyük bilim adamından biri olarak kabul edilen Apollonius konik kesitleri üzerine bugün de hayranlık uyandıran 8 kitaplık mükemmel bir eser bırakmıştır insanlığa. (Bu 8 kitaptan 8 cisi bugüne kadar bulunamamıştır).
Bütün zamanların en büyük bilim adamlarından biri olarak kabul edilen Siraküs’lü Arşimed (M.Ö. 287-212) de bir rivayete göre Museum da yetişmiştir. En azından bir süre burada kaldığı bilinmektedir. Arşimed icat ettiği mekanik aletlerinin yanı sıra, Öklid’in geometride yaptığını bir ölçüde mekanikte yapmış, mekaniğin ve hidrostatiğin temel ilkelerini yasalaştırmaya çalışmıştır. Matematiğe katkıları, silindir ve küre hakkında çalışmaları; başlangıcı Eudox’a giden, “exhaustion” yöntemiyle bir çok şeklin alanını hesaplamış olmasını sayabiliriz. Bu, bugün matematikte entegral olarak bilinen kavramın başlangıcıdır. Eudox’tan zamanımıza yazılı hiçbir eser kalmamıştır. Bu nedenle, belgeli olarak, bu yöntemin ilk olarak kullanıldığı yer Arşimed’in eserleridir.
Arşimed bu yöntemle, bir dairenin içine ve dışına düzgün 96 kenarlı çokgenler çizip, onların alanlarını hesaplayarak, pi sayısının 3,10/71 ile 3,10/70 arasında bir değeri olduğunu hesaplamıştır. Bu da pi’ nin virgülden sonra ilk üç rakamını doğru olarak vermektedir. O zamana kadar pi sayısının bilinen değerleri deneysel, ölçme yoluyla elde edilen değerler idi. Museum da yetişen ve tarihin en önemli astronomlarından biri olarak kabul edilen bir bilim adamı da, batılıların Potolemy, doğuluların Batlamyüs olarak bildiği Claudius Potolemy’dir (M.S. 85-165). Batlamyüs, uzun yıllar süren gözlemlerden sonra, Hipparkus gibi daha önce yaşamış olan başka astronomların da gözlemlerini de kullanarak, tutarlı bir evren sistemi oluşturmuş; geniş astronomik ölçüm cetvelleri ve bir yıdız kataloğu hazırlamıştır. Batlamyüs’ün sisteminde, dünya sistemin merkezindedir; güneş, ay ve diğer gezegenler dünya etrafında çembersel bir yörüngede dönmektedirler. Arapların, en büyük manasına “almagest” dedikleri ve Yunanca ismi “matematica” olan ünlü astronomi kitabı 15 asır boyunca astronomi ile ilgilenen bütün bilim adamlarının başucu kitabı olarak kalmıştır.
Yunanlılar alfabelerinin harflerini rakam olarak kullanmışlardır. Bu sistemde sayıların yazılımı Romen rakamlarının yazılımına benzer ama daha gelişmiş bir sistemdir. Yunun matematiği büyük ölçüde geometri olarak geliştiği için çok yetkin bir rakam sistemine ihtiyaç duymamışlardır.
Bu kısımda anlatmaya çalıştığımız dönemde yaşamış 100 den fazla matematikçinin ismi ve bazı çalışmaları zamanımıza gelmiştir. Bu da o dönemdeki bilimsel faaliyetlerin yoğunluğu, devlet ve toplum nezdindeki önemini göstermektedir.
Yunan matematiğini değerlendirecek olursak, temel özellikleri şunlardır. a) Yunanlılarla, matematik zanaat düzeyinden sanat düzeyine geçmiştir. Bu matematikte, günlük hayatta işe yararlılık değil, derinlik, estetik ön plandadır. b) Yunan matematiği bugünkü manada moderindir; bugün biz nasıl matematik yapıyorsak, o zaman onlar da böyle yapıyorlardı. Zaman içinde ispat anlayış ve standartları değişmektedir; ama Öklid’in verdiği ispatlar, bugün de büyük ölçüde geçerlidir.
Şimdi bu dönem nasıl bitti, bir sonraki dönem nasıl başladı; kısaca bunu anlatmaya çalışacağım. Bu dönemi sona erdiren iki önemli etmen Roma’nın yükselişi ve Hıristiyanlığın Roma imparatorluğunun resmi dini oluşudur. M.Ö. 150 yıllardan itibaren Roma imparatorluğu genişlemeye başlamıştır. M. Ö. 30 lu yıllara gelindiğinde her üç Yunan kültür bölgesi de artık Romalıların hükmü altındadır. Her ne kadar da idari ve askeri olarak Romalılar Yunan kültür bölgelerine hakim iseler de, kültürel olarak Roma imparatorluğu bir Yunan kolonisidir; az-çok, Yavuz Sultan Selim’den sonra, Osmanlıların Arap dünyasına hükmetmelerine karşın, kültürel açıdan bir Arap kolonisi durumunda oldukları gibi. Bu nedenle, Romalılar Yunan kültür kurumlarının (Platonun akademisi, Bergama Okulu, Museum gibi) faaliyetlerine devam etmelerine müsaade etmişlerdir. İskenderiye’nin alınışı sırasında İskenderiye kütüphanesi yanmıştır ama Bergama kütüphanesinden gönderilen 200.000 kitapla İskenderiye kütüphanesi tekrar oluşturulmuştur.
Romalılar Museum daki bilim adamların maaşlarını devlet hazinesinden karşılamayı sürdürmüşlerdir. Ne var ki, zamanla ekonomik durumun kötüleşmesi eğitim kurumlarında etkileyecektir. Bu kurumlara en büyük darbeyi vuran ise Hrıstiyanlık olmuştur. Hrıstiyanlık ilk 300 yıl yasaklı olduğu için yer altında gelişmiştir. Bu dönemde Hrıstiyanlık çok hoş görülü ve bir eşitlik dinidir. Bu nedenlerle, geniş bir taraftar kitlesi bulabilmiştir. M.S. 300 gelindiğinde, Hristıyanlığın gelişmesinin önlenemeyeceğini anlayan Roma imparatoru I. Constantin 313 de Hristıyanlığın üzerindeki yasağı kaldırmış, Roma’dan ayrılarak, Roma imparatorluğunun başkentini İstanbul’a (Constantinople) taşımıştır. 380 lerde, Hristıyanlık Roma imparatorluğunun resmi dini olmuştur.
Bu tarihten itibaren, Kilise yavaş-yavaş sosyal ve eğitim hayatına hakim olmaya, Hristıyan öğretisinin dışında hiç bir öğretiye hoş bakmamaya başlamıştır. 390 de Kril (Cril) isimli bir papazın İskenderiye kütüphanesini ateşe vermesiyle başlayan girişim, Museum’da çalışan bilim insanlarına saldırılara dönüşmüş; 421 de Museum’da ders veren ve tarihin ilk kadın matematikçisi olarak bilinen Hypatia [Hypatia, tanınmış bir matematikçi olan İskenderiyeli Heron’un kızıdır] yobaz Hrıstiyanlar tarafından linç edilerek öldürülmüştür. Bu olaydan sonra Museum kapanmış ve 641 de Müslümanların Mısırı fethi sırasında da tamamen yanmıştır. Bu okulun kapanmasından sonra, Museum da çalışan bilim adamları kitaplarını alarak, Sasanilerin hakim oldukları güneydoğu Anadolu (Harran, Urfa) ve Mezopotamya içlerine, Cundişapur’a (şimdiki İrak’taki Beth-Lapat), göçmüşlerdir. 529 yılında da Bizans imparatoru Jüstinyen Atina’ da bulunan Platon’un akademisini kapatmıştır. Bu tarih Yunan kültürünün hakim olduğu bir dönemin bitişi, karanlık çağın başlangıcıdır. Akademinin kapanmasından sonra orada çalışan bilim insanlarının bir kısmı da doğuya göçmüşlerdir. Bu göçler kitlesel göçler değildi; bugün olduğu gibi o gün de bilim insanları kitle oluşturacak kadar çok olmamışlardır. Bu göçlerin Haçlı seferlerine kadar zaman -zaman devam ettiği anlaşılmaktadır. Doğuya göçen bu bilim adamları, Yunan kültürüne aşina olan ortamlarda, özellikle Nestorien- Süryani toplumlarda daha uzun yıllar öğretilerini sürdürmeye, bilim meşalesini söndürmemeye çalışacaklardır. İslam biliminin temelinde bu insanların emeği, onların yaptıkları çeviriler vardır. Böylelikle bundan sonraki döneme, Müslümanların hakim olduğu döneme gelmiş bulunuyoruz.
3- Islam Dünyasında ve Orta Çağda Matematik
611 den, Hz. Muhammet’in peygamberliğini açıklamasından yüz yıl sonra, 711 ‘re gelindiğinde, İslam imparatorluğu, doğuda Çin sınırına ve Hindistan içlerine, batıda, kuzey Afrika’dan ve Cebel-Tarık’tan geçerek, Pirene dağlarına dayanıyordu. Bu arada, İstanbul kuşatılmış (675-677), doğu ve güneydoğu Anadolu’nun bir kısmı fethedilmiş, Kıbrıs ve Sicilya alınmış, devasa bir imparatorluk oluşturulmuştu. Bu imparatorluk Şamdan, Emevi hanedanlığı tarafından yönetilmekteydi. Emevi’lerin Arap olanla olmayanlara farklı muameleleri orta Asya’da, Ebu Müslim Horasani’nin yönettiği büyük bir isyan çıkmasına neden oldu. Bu isyan Basra civarında başlayan Abbas oğullarının isyanıyla birleşerek Emevi hanedanlığına son verdi. Kıyımdan kurtulan Emevi’lerden Abdurahman Endülüs’te Emevi hanedanlığını daha bir süre devam ettirecektir.
İslam dünyasına bilim, 750 den sonra, Abbasiler zamanında girmeye başladı. O tarihlerde, Basra bölgesinden yayılmaya başlayan ve İslam rasyonelizimi olarak ta bilinen Mutezile (=ayrılanlar) tarikatı, bu tarikatın Vasıl bin Ata gibi o zamanki önderlerinin halife Mansur’a ve Şia imamlarına yakın olmaları, bu tarikatın devlet ve halk tarafından benimsenmesine neden oldu. Doğruların akıl ve rasyonel düşünceyle bulunacağını savunan bu akım, İslam dünyasına bilimin girmesinin düşünsel zeminini oluşturmuştur. Abbasiler Şam’ı başkent yapmayarak, Bağdat’ı kurup orasını kendilerine başkent yapmışlardır. Abbasi halifeleri Mansur, Harun Reşit ve El-Mamun, Bağdat’ta “Dar’ül Hikmet “ ( Aklın Evi) diye bilinen, İskenderiye’deki Museum benzeri bir medrese kurmuşlar, büyük bir çeviri faaliyetine girişmişlerdir. Yukarıda da belirtildiği gibi, ilk çeviriler, Yunan dil ve kültürüne vakıf bölgelerdeki, özellikle Cundişapur ve güneydoğu Anadolu’daki Süryani ve Mecusiler ( Harranlı Tabit ibni Kurra ve çocukları gibi) tarafından yapılmıştır. Çeviriler sadece Yunanca’dan değil, Hindçe’den, Pehlevice’den, İbranice’den… de yapılmıştır. Böylelikle geniş bir kütüphane oluşturulacaktır.
Bu çevirilerin çeşitli kaynaktan yapılmış olmasından da anlaşılacağı gibi, İslam matematiği Yunan geleneğinin bir devamı olmaktan çok, Yunan, Mezopotamya ve Hind matematiklerinin bir sentezidir. Sayı sistemleri, aritmetik, trigonometri ve cebir, daha çok Mezopotamya ve Hind geleneklerine; geometri ise Yunan geleneğine dayanır. Zamanımıza, 750-1450 yılları arasında yaşamış 50 kadar matematikçi-bilim adamının ismi ve çalışmaları gelmiştir. Unutmamak gerekir ki, o tarihlerde yaşamış olan bilim insanlarının çoğu, zamanın bütün bilimleriyle uğraşmış, ya da en azından 3-4 bilim dalında eser vermiş insanlardır. Bu 50 kadar matematikçiden sadece 4-5 tanesinin çalışmaları hakkında bilgi vereceğim. Bunun bize o dönem matematiği hakkında yeterli bir fikir verecektir sanırım.
- 611 den, Hz. Muhammet’in peygamberliğini açıklamasından yüz yıl sonra, 711 ‘re gelindiğinde, İslam imparatorluğu, doğuda Çin sınırına ve Hindistan içlerine, batıda, kuzey Afrika’dan ve Cebel-Tarık’tan geçerek, Pirene dağlarına dayanıyordu. Bu arada, İstanbul kuşatılmış (675-677), doğu ve güneydoğu Anadolu’nun bir kısmı fethedilmiş, Kıbrıs ve Sicilya alınmış, devasa bir imparatorluk oluşturulmuştu. Bu imparatorluk Şamdan, Emevi hanedanlığı tarafından yönetilmekteydi. Emevi’lerin Arap olanla olmayanlara farklı muameleleri orta Asya’da, Ebu Müslim Horasani’nin yönettiği büyük bir isyan çıkmasına neden oldu.
Bu isyan Basra civarında başlayan Abbas oğullarının isyanıyla birleşerek Emevi hanedanlığına son verdi. Kıyımdan kurtulan Emevi’lerden Abdurahman Endülüs’te Emevi hanedanlığını daha bir süre devam ettirecektir. İslam dünyasına bilim, 750 den sonra, Abbasiler zamanında girmeye başladı. O tarihlerde, Basra bölgesinden yayılmaya başlayan ve İslam rasyonelizimi olarak ta bilinen Mutezile (=ayrılanlar) tarikatı, bu tarikatın Vasıl bin Ata gibi o zamanki önderlerinin halife Mansur’a ve Şia imamlarına yakın olmaları, bu tarikatın devlet ve halk tarafından benimsenmesine neden oldu. Doğruların akıl ve rasyonel düşünceyle bulunacağını savunan bu akım, İslam dünyasına bilimin girmesinin düşünsel zeminini oluşturmuştur. Abbasiler Şam’ı başkent yapmayarak, Bağdat’ı kurup orasını kendilerine başkent yapmışlardır. Abbasi halifeleri Mansur, Harun Reşit ve El-Mamun, Bağdat’ta “Dar’ül Hikmet “ ( Aklın Evi) diye bilinen, İskenderiye’deki Museum benzeri bir medrese kurmuşlar, büyük bir çeviri faaliyetine girişmişlerdir.
Yukarıda da belirtildiği gibi, ilk çeviriler, Yunan dil ve kültürüne vakıf bölgelerdeki, özellikle Cundişapur ve güneydoğu Anadolu’daki Süryani ve Mecusiler ( Harranlı Tabit ibni Kurra ve çocukları gibi) tarafından yapılmıştır. Çeviriler sadece Yunanca’dan değil, Hindçe’den, Pehlevice’den, İbranice’den… de yapılmıştır. Böylelikle geniş bir kütüphane oluşturulacaktır. Bu çevirilerin çeşitli kaynaktan yapılmış olmasından da anlaşılacağı gibi, İslam matematiği Yunan geleneğinin bir devamı olmaktan çok, Yunan, Mezopotamya ve Hind matematiklerinin bir sentezidir. Sayı sistemleri, aritmetik, trigonometri ve cebir, daha çok Mezopotamya ve Hind geleneklerine; geometri ise Yunan geleneğine dayanır. Zamanımıza, 750-1450 yılları arasında yaşamış 50 kadar matematikçi-bilim adamının ismi ve çalışmaları gelmiştir. Unutmamak gerekir ki, o tarihlerde yaşamış olan bilim insanlarının çoğu, zamanın bütün bilimleriyle uğraşmış, ya da en azından 3-4 bilim dalında eser vermiş insanlardır. Bu 50 kadar matematikçiden sadece 4-5 tanesinin çalışmaları hakkında bilgi vereceğim. Bunun bize o dönem matematiği hakkında yeterli bir fikir verecektir sanırım.
İlk ele alacağımız matematikçi Muhammet ibni Musa al-Harazmi’dir (780-850). İsminden güney Özbekistan’da doğduğu anlaşılıyor. Hayatı ve nerelerde okuduğu hakkında güvenilir bir bilgi yoktur. 810 dan sonra Bağdat’ta Dar’ül Hikmet’in kütüphanecisi olarak çalışmaya başlamış ve 4 kitap yazmıştır. Bunlardan biri coğrafya, biri astronomi, biri aritmetik diğeri de bir cebir kitabıdır. Biz bu son ikisi hakkında biraz bilgi vereceğiz. Al-Harazmi’nin en ünlü kitabı “ Al-Cebir ve Al-Mukabele” dır. Bu “indirgeme ve denkleme” manasına gelen başlık, daha sonraları “Cebir” (veya Algebra) olarak kısaltılacaktır. Bu kitapta Al-Harazmi ikinci dereceden bir polinomu katsayılarının işaretine göre 6 sınıfa ayırarak, sistematik olarak, her sınıf için, köklerin nasıl bulunacağını “algoritmik” bir yaklaşımla göstermektedir. Örnek olarak, bizim bu gün x^2-10x-4=0 olarak yazacağız bir polinomu x^2=10x+4 şeklinde yazmaktadır ve bu polinomun köklerini bulmak için adım -adım ne yapılması gerektiğini söylemektedir. Unutmamak gerekir ki o tarihlerde henüz negatif sayılar kullanılmıyor ve sayı uzunluk olarak düşünülmektedir. Müslümanlar, burada söz konusu olan dönemde (750-1450), bir istisna (Abu Waffa (940-998)) dışında, negatif sayıları hiç kullanmamışlardır. Al-Harazmi’nin, verilen bir polinomun kökünü bulmak için, izlemiş olduğu adım-adım yaklaşıma günümüzde “algoritmik” yaklaşım denmektedir; bu sözcük Al-Harazmi’nin ismi bozularak türetilmiştir. Al Harazmi, daha sonra, algoritmik olarak bulduğu kökü geometrik olarak da bularak yaptıklarını doğrulamaktadır. Son olarakta Al-Harazmi kitabında, bu yöntemin miras hesaplarına pratik uygulamalarını vermektedir. Bu kitap 1140 larda Latinciye çevrilmiş ve 1600 lere kadar batı okullarında kullanılmıştır. Bu eser, hakkında çok tartışma olan bir eserdir. Kimilerine göre, cebir’in esas babası Diofand’dır; Al-Harazmi’nin cebiri Mezopotamya matematiğinden daha ileri düzeyde değildir. Bu da büyük ölçüde doğrudur. Kimileri ise, bu eserin her şey ile orijinal olduğunu savunmakta.
Açık olan bir şey varsa, o da bu eserden sonra, matematikte “cebir” diye bir ana bilim dalının ortaya çıkmasıdır. Önemli olan diğer bir husus da, algoritmik yaklaşım dediğimiz, bu kitabın yöntemidir. Al-Harazmi’nin diğer kitabı bir “Hesap” kitabıdır. Bu kitabın Arapçası günümüze ulaşmamıştır; var olan bir Latince çevirisidir. Bu kitapta, Al- Harazmi bugün kullandığımız Hind-Arap rakamları olarak bilinen ( 1,2,…,9, 0) rakamları tanıtmakta; onlarla sayıların nasıl yazıldığını, toplama, çarpma gibi işlemlerin nasıl yapıldığını anlatmaktadır. Burada sıfır bir “ boşluk dolduran sembol” olarak kullanılmıştır, sayı olarak değil. Sayı olarak, sıfır ilk kez, 876 de Hindistan’da kullanılmıştır. Daha önce de kullanıldığı hakkında bilgiler vardır ama herkesin hem fikir olduğu tarih bu tarihtir. Negatif sayıların da Hindistan’da 620 lerde kullanıldığı bilinmektedir ama az-çok yaygın olarak kullanılmaya başlanmaları 1600 ler den sonradır.
Çalışmalarına deyineceğimiz ikinci matematikçi Ömer Hayyam’dır (1048-1131). Nişabur da doğan Ömer Hayyam, 1073 den sonra, İsfahan’da kurulan rasathanede, Selçuk hükümdarı Melik Şahın “müneccim başı” olarak çalışmaya başlamış. Zamanımıza Rubailerinden başka bir cebir kitabı ve astronomiyle ilgili çalışmalarından da bazı kısımlar kalmıştır. Cebir kitabında, üçüncü dereceden polinomların bir sınıflandırmasını yaparak, konik kesitlerini kesiştirerek, bu polinomların köklerini geometrik olarak bulmaya çalışmıştır. Örnek olarak, x^3+ax^2+bx+c=0 polinomunun kökünü bulmak için x^2=2dy alarak 2dxy+2ady+bx+c=0 hiperbolünü elde eder. Bu hiperbol ile y=x^2/2d parabolünun kesişme noktaları baştaki polinomun köklerini verecektir. Bu çalışmada önemli iki nokta, üçüncü dereceden bir polinomun birden çok kökünün olabileceğini anlamış olması ve kökleri bulmak için konik kesitlerini kullanması gerektiğini görmüş olmasıdır. Bu da Ömer Hayyam’ın Apolyonus’un konik kesitleri gibi zor bir konuya derinlemesine vakfı olduğunu göstermektedir. Ömer Hayyam astronom olarak, gözlem ve ölçümlere dayalı, bir takvim reformu yaparak, yeni bir takvim (Celali takvimi) hazırlamıştır. Bu gayeyle, Ömer Hayyam bir güneş yılının uzunluğunu 365.24219858156 gün olarak hesaplamıştır. Şimdi bilinen, bir yılın 365.242190 gün olduğunu ve her 70-80 senede virgülden sonraki 6. rakamın değiştiğini burada belirtelim.
Çalışmaları hakkında bilgi vereceğimiz üçüncü matematikçi Şarafeddin al-Tusi (1135-1213) dır. İsminden, İran’ın Tus şehrinde doğduğu anlaşılmaktadır. Muhtemelen Meşed yada Nişabur’da yetişmiştir. Şam, Halep, Musul ve Bağdat da matematik okutmuştur. Önemli bir cebir kitabının yazarıdır. Ş. Al-Tusi de, Ömer Hayyam gibi üçüncü dereceden polinomların köklerini bulmak için uğraşmıştır. Harazmi’nin izinden, Ş. Al-Tusi üçüncü dereceden denklemleri 25 sınıfa ayırarak, cebirsel yaklaşımla, onların köklerini bulmaya çalışmıştır. Bugünkü notasyonla, x^3-ax=b gibi bir denklemin belli bir aralıkta çözümünün olabilmesi için, b nin x^3-ax in maksimumu ile minimumu arasında olması gerektiği anlayan Ş. Al-Tusi, bu ifadenin maksimumun bu ifadenin “türev” inin sıfır olduğu yerde araması gerektiğini anlamıştır. Kimi yazarlara göre bu türevin keşfidir. Ne yazık ki o zaman bu keşfin değeri anlaşılmamış, türevin farkına varılmamıştır. Matematiğin en önemli keşiflerinden olan türev, 1636 de Fermat tarafından tekrar keşfedilecek ve bu da, analitik geometri ile beraber, kalkülüsün doğumuna neden olacak ve matematikte bir devrim yaratacaktır.
Ele alacağımız 4. matematikçi, büyük Tusi, Nasireddin Al-Tusi’dir (1201-1274). O devir İslam dünyasının en büyük bilim adamlarından olan N. Al-Tusi, Tus ve Nişapur’da okumuştur. Mantık, Ahlak, Felsefe, Astronomi ve Matematik kitapları yazmıştır. Hayatının önemli bir kısmını, Hasan El-Sabahın örgütünün merkezlerinden biri olan, ve çok iyi bir kütüphanesi olduğu bilinen, Alamut kalesinde araştırma yaparak geçirmiştir. Bu kale 1256 da Hülagü han tarafından alındıktan sonra, Hülagü hanın müneccim başı olmuş, 1262 den sonrada Marageh’de ( Güney Azerbaycan’da, Tebriz civarında ) Hülagü hanın emriyle kurulan rasathanede araştırmalarını sürdürmüş ve bir ziç, Ziç-i-İlhani’ yi hazırlamıştır. Ziçler, astronomik hesaplar için gerekli olan, sinüs cetvelleridir. N. Al-Tusi’nin astronomi ile ilgili çalışmaları, Batlamyüs’den sonra Copernicus’un çalışmalarına kadar, astronomi hakkında en önemli çalışmalardan biri olarak kabul edilir. Matematikle ilgili en önemli çalışması, düzlem ve küresel trigonometri ile ilgili çalışmalarıdır. Bu eserden sonra trigonometri, astronomi için bir araç olmaktan çıkıp, matematiğin bir ana dalı olmuştur. Bunun dışında, Yunanca’dan çeviri çok sayıda matematik kitaplarına izah ve yorumlar yazmış; bir sayının n inci kökünü bulmak için çalışmalar yapmıştır. Batılı matematikçi ve astronomiçilerin, eserlerinden en çok yararlandıkları islam dünyası bilim adamlarının başında N. Al-Tusi gelir.
Çalışmalarından bahsedeceğimiz bu dönemin son matematikçisi Cemşit Al-Kaşi’ dır (1380-1429). Kaşan (Iran) da doğmuştur. Kaşan’da yetiştiği anlaşılan Al-Kaşi, 1420 den itibaren ölene kadar, Uluğ Bey ve Kadızade ile Semarkand’ ta Uluğ Bey medresesinde ve rasathanesinde çalışmıştır. Timurleng’in torunu olan Uluğ Bey (1393-1449) iyi bir matematikçi, bilim aşığı bir hükümdardı. O tarihlerde Uluğ Bey’ in medresesinde 60 civarında zamanın en iyi bilim adamları ders vermekte ve araştırma yapmaktadır; bu metrese, pozitif bilimlerin okutulduğu ve bilimsel bir saygınlığı olan İslam ülkelerindeki son metresedir. Al-Kaşi, Uluğ Bey’le beraber, N. Al-Tusi’nin ziçlerinden de yararlanarak, Ziç-i-Hakani olarak bilinen Uluğ Bey’in ziçlerini hazırlamıştır. Bu ziç’te 1 den 90 dereceye kadar olan açıların, birer dakika arayla, sinüsleri verilmiştir. Bu da 60×90=5400 giriş demektir. Her açının sinüsü, virgülden sonra 8. haneye kadar verilmiştir. Bu iş bugünün imkanlarıyla bile, kolayca yapılacak bir iş değildir. Ayrıca bu ziç, güneş, ay ve gezegenlerin konumu ve hareketleri hakkında detaylı bilgi ve gözlem tabloları içermektedir. Al-Kaşi muhteşem bir hesap yeteneği olan matematikçidir. Yarı çapı 1 olan bir daireyi 3×2^28=805. 306. 368 kenarlı bir poligonun içine oturtarak, pi sayısının virgülden sonra 16 hanesini ( 10 ve 60 tabanlı sayı sistemlerinde) doğru olarak vermiştir. Bu rekor ancak 200 yıl sonra kırılabilecektir. Al-Kaşi, içeriğinin zenginli, ispatlarının açıklığı ile orta çağın en iyi kitaplarından biri olarak kabul edilen “Aritmetiğin Anahtarı” başlıklı bir kitabın da yazarıdır. Ondalık kesirlerle 4 işlemin nasıl yapılacağını açıklayan da Al-Kaşi’dir. Al-Kaşi’nin ölümünden sonra Uluğ Bey’e ziçlerini tamamlamasına ve gerekli izahların yazılmasına, Al-Kaşi ve Kadızade’ nin öğrencisi olan, Ali Kuşçu yardım etmiştir. 1449 da Uluğ Bey’in, devlet işleriyle uğraşmıyor, hayırsız bilimle uğraşıyor diye öz oğlu ve akrabaları tarafından öldürülmesinden sonra, Uluğ Bey’in medrese ve rasathanesi de çökmüştür. Bu İslam dünyasındaki son önemli positif bilim merkezinin sönmesidir. Bu son ismi geçen kişiler İslam dünyasının matematikçi diyebileceğimiz son bilim adamlarıdır. 1450 den 1930-40 lar’a kadar İslam dünyasında orijinal bir çalışma yapmış ve matematikçi diye nitelendirebileceğimiz bir kişinin ismi bilim tarihinde geçmemektedir.
Bu bölümü Müslümanların matematiğe katkılarının bir değerlendirmesiyle bitireceğim. Müslümanların matematiğe katkılarını, bu konuda çok çelişkili yargıların olması nedeniyle, değerlendirmek çok zordur. Müslümanların matematiğe katkıları kimi yazarlar tarafından sıfırlanırken, kimi yazarlar tarafından da göklere çıkartılmaktadır. Kimi yazarlara göre Müslümanların matematiğe hiç bir katkısı olmamıştır; bütün yaptıkları bir buzdolabı görevi görmekten ibarettir. Yunanlıların pişirdiklerini, Avrupalılar onu yiyecek düzeye gelene kadar saklamışlar, günü geldiğinde de Avrupalılar onu alıp yemişlerdir. Kimilerine göre ise, Müslümanların matematiğe ve astronominin gelişmesine kapsamlı özgün katkıları olmuştur; bu gün batılı bilim adamlarının adını taşıyan bir çok teorem veya sonuç daha önce Müslümanlar tarafından bulunmuştur. Görülen o ki a) Müslümanlar sulayıp büyüttükleri ağaçların meyvelerini toplayamamışlar; ve b) Müslümanların bilime katkıları yeteri kadar araştırılıp değerlendirilmemiştir. Bu işi yapanların çoğunlukla yine batılı bilim tarihçilerin olduklarını unutmamak gerek. Kendi bildiğim kadarıyla, Müslüman matematikçilerin Küresel geometriye, cebire, sayılar teorisine, trigonometri ve astronomiye özgün katkıları olmuştur ve bu katkılar hiçte küçümsenecek ölçülerde değildir. Ayrıca, insanlığın ortak ürünü olan bilimin önemli bir halkası, eskiyle yeniyi bağlayan halkası, İslam bilimidir. Bu halka olmadan, bilimin bugünkü düzeye gelmesi herhalde mümkün olmayacaktı.
Bir sonraki bölüme geçmeden “İslam ülkelerinde bilim niye çöktü; batıya bilim nasıl girdi “ soruları hakkında bir kaç şey söylemem gerekir. Bu sorular, tek bir kişinin yanıtlayabileceği sorular değildir; ancak geniş ve çok yönlü bir ekip bu sorulara tatmin edecek cevap verebilir. Şimdi söyleyeceklerim, başka biri için, İslam ülkelerinde bilimin çöküşünün en derin nedenleri olmayabilir. Bu konu çok tartışılan bir konudur, bildiginiz gibi. Şimdi söyleyeceklerim sadece kendi görüşlerimi yansıtmaktadır. a) Haçlı seferleri İslam dünyasında, bugün de kanayan, derin yaralar açmıştır. İlk haçlı seferleri sırasında yapılan büyük katliamlar ve yamyamlık olayları, bölge insanlarını derin bir ümitsizlik, çaresizliğe ve bunalıma sokmuştur. Niçin bu duruma düştüklerini sorgulayan insanlar, İslam’ın başında olduğu gibi din duygularının güçlendirilmesi, dini ve imanı için ölecek insanların yetiştirilmesi gerektiği kararına varmışlar. İmam Gazalinin görüşlerinin de etkisiyle, bu tarihlerde, 1100-1150 arası, İslam dünyasında akli bilimlerden nakli bilimlere bir dönüş olmuştur. Bu olayın üzerine, 1250 lerden itibaren başlayan Moğol istilası sonucu, eğitim kurumları ve kütüphanelerin en önemlilerinin yok oluşunun eklenmesi; benzeri durumun Endülüs’ün kademeli olarak Hrıstiyanların eline düşmesi sonucunda da olması, bu geçişi kolaylaştırmış, derinleştirmiştir ve geri dönülmesi neredeyse olanaksız bir noktaya getirmiştir. Ancak haçlı seferleri ve Moğol istilası gibi derin izler bırakan bir olay bu gidişi tersine çevirebilirdi; bu da 1918 de yaşanan son “haçlı” seferiyle yaşanmıştır. Atatürk’ün “Hayatta en hakiki mürşit ilimdir, fendir; bunun dışında mürşit aramak, gaflettedir, delalettir “ sözü, nakli bilimlerden akli bilimlere dönüşü simgeler. b) Medreseler İslam dünyasında daha çok 1150 den sonra çoğalmaya başlamışlar ve “nakli bilim” ( ya da “hayırlı bilim”) eğitimi veren okullar olarak çoğalmışlardır.
Osmanlı İmparatorluğuna Araplardan geçen bilim geleneği akli ilim değil, nakli bilim geleneğidir. c) Medreseler, vakıflara bağlı olmalarına rağmen, kurumsallaşıp, gelişmemiş; aksine her türlü yeniliğe karşı çıkan, yobaz üretim merkezi olmuşlardır. d) Din’i ve din’i ulemayı kendine ideolojik dayanak yapan yönetici sınıf, ulemayı imtiyazlı bir sınıf konumuna getirirken, pozitif bilimlerle uğraşanları ezmişlerdir. e) İmtiyazlı bir sınıf konumuna gelen, devlet ve halk nezdinde büyük bir saygınlığa erişen ulema sınıfı, pozitif bilimlerin yeşermesine, bu bilimlerle uğraşan insanların toplum içinde saygın bir konuma gelmelerine mani olmak için açık-gizle her türlü çabayı göstermişlerdir ve bunda da başarılı olmuşlardır. f) Dar bir ortamda yetişen, dünya görüşünden yoksun, ülke ekonomisiyle kendi ekonomisini karıştıran idareci sınıfları bilimle teknoloji arasındaki ilişkiyi hiç bir zaman anlamamış; ülkelerinin geri kaldığını ancak askeri yenilgilerden sonra anlayabilmişlerdir. Bu durumda, köklü reform yapmaları gerekirken, düzen bozulur korkusuyla, koyma suyla değirmen döndürmeye çalışmışlar, orduyu düzeltmek için bir-kaç yabancı uzman çağırmakla yetinmişlerdir. İslam ülkelerinde, özellikle Türkiye’de, nakli bilimlerden akli bilime dönüş, yukarıda 9. haçlı seferi olarak nitelediğim, bütün İslam ülkelerinin batının işgaline uğradığı, 1.ci dünya savaşından, özellikle1930 lar’dan sonradır. Bu ülkelerde, bilimsel gelişmeler ancak bu tarihten sonra, emekleye-emekleye de olsa, gelişmeye başlamıştır.
Batıya matematik nasıl girdi sorusuna gelince, bu üç yoldan olmuştur. a) Ortadoğu’da 4 krallık kurup, 200 yıla yakın bir süre Ortadoğu’da kalan haçlılar vasıtasıyla, b) Arap medreselerinde okuyan batılı öğrenciler vasıtasıyla; ve c) Endülüs’ten. Büyük kapının Endülüs olduğu gözükmektedir. Her ne kadar da Endülüs’te önemli matematikçiler yetişmemiş olsa da, Endülüs’te eğitimin yaygın; ortamın bilim için uygun olduğu, felsefe, kimya tıp, gibi bilim dallarda oldukça ileri olduğu bilinmektedir. Örneğin, 11. asırda Kordoba’da 400 bin kitablık merkez kütüphanesi, 17 medrese ve bir çok halk kütüphanesi bulunuyordu. Buralarda Hristıyan ve Musevi öğrenciler okuyabiliyordu. Toleodo İspanyolların eline geçtiğinde (1100), Toleodo piskoposu, büyük bir çeviri bürosu kurarak, çok sayıda bilimsel eseri, Arap metreselerinde yetişmiş olan Musevi çevirmenler vasıtasıyla, Arapçadan Latince’ye çevirtmiştir. 12. asra kadar Avrupa’daki okullar, din ağırlıklı skolastik eğitim verilen manastır veya katedral okullarıydı. 12. asrın ortalarından itibaren İtalya’da (Bolonya, Padova), öğrencilerin “universita” dedikleri dernek türü kurumlarda bir araya gelerek, eğitim için birleşmiş, böylelikle daha sonra üniversite olacak kurumların çekirdeklerini dikmişlerdir.
Bu kurumlarda ders veren hocalar Arap metreslerinde okumuş batılı (İtalyan) gençlerdi. Daha sonra bu kurumlarda okuyan Avrupalı öğrenciler Almanya’da (Köln), Fransa’da (Sorbone) ve İngiltere’de ( Oxford, Cambrigde) üniversitesi olacak olan eğitim kurumlarını kuracaklardır. Bu dönemde Kutsal Roma-Germen imparatoru olan 2. Frederik’in açık görüşlü, bilime değer veren bir insan oluşunun ve, 1200 lerin başında kurulmuş olan, Fransican tarikatının katkılarının da pozitif bilimlerin Avrupa’ya’ya girmesinde ve gelişmesinde etkili olmuş olduğunu belirtmek gerekir. 1200 ile 1500 ler arası Avrupalıların bilimsel kaynakları Arapça eserlerdi. Uğraştıkları sorular da bu kitaplarda Müslüman matematikçilerin uğraştığı sorulardı. Bunlar da, bazı geometri soruları, 3. dereceden polinomun köklerini bulma sorunu, sayılar teorisiyle ilgili sorulardır. 1450 lerden sonra, İstanbul’ dan İtalya’ya giden kitaplardan, matematiğin Yunanca kaynaklarına inmeye, Yunanca kaynaklardan çeviri yapmaya başlıyacaklardır; 1600 lerden sonra Arapça kaynaklar büyük ölçüde terk edilecektir. Avrupa’da matematikte özgün gelişmeler 1500 lerden sonradır. Şimdi biraz bunlardan bahsetmemiz gerekiyor.
Batıya bugünkü kullandığımız Hind-Arap rakamları (1,2,…,9, 0) 1200 lerin başında Fibonacci’nin ( Leonordo de Pisa, 1175-1250) yazdığı “ Liber Abacci” isimli kitabıyla girmiştir. Bu kitapta Fibonacci, kendinden 400 yıl önce Harazmi’nin yaptığı gibi, bu rakamlarla sayıların nasıl yazılacağını, dört işlemin nasıl yapılacağını izah etmektedir. Bu rakamlar batıda günlük hayatta 16. asra kadar çok yaygın olarak kullanılmamış, zaman -zaman da yasaklanmıştır. Bu rakamların halk arsında yaygın olarak kullanılması Fransız devriminden sonra olmuştur. 1200 lerden 1500 lere kadar kayda değer özgün bir çalışma yoktur. 1500-1600 arası iki önemli çalışma a) Tartaglia’nın (1499-1557) bulduğu ama Cardano’nun (1501-1576) aşırarak yayımladığı üçüncü dereceden polinomların cebirsel olarak köklerinin bulunmasıdır. Kompleks sayılar ilk olarak 3. derecede polinomların kökünü veren formülde, o tarihlerde anlaşılmamış olsa da, ortaya çıkmıştır. Daha sonra Bombelli (1526-1572) cebir kitabında bazı tip kompleks sayılara yer verecek, onlarla nasıl işlem yapılacağını anlatacaktır. b) Diğer önemli çalışma ise, F. De Viete (1540-1603) in cebir kitabıdır. İlk olarak bu kitapta, cebir, sözel olmaktan çıkıp, sembolleşmeye başlamıştır. Viete’in kitabında sessiz harfler bilinen kantiteler, sesliler de bilinmeyenler için kullanılmıştır. Sabitler için a,b gibi alfabenin ilk harflerinin; bilinmeyenler için de x,y gibi alfabenin son harflerinin kullanılması Descartes’le başlayacaktır.
1600-1700 arası matematikte önemli gelişmelerin olduğu yıllardır. Bu asrın üç önemli gelişmesi şunlardır: a) Türevin bulunması. P. Fermat’nın (1601-1665), 1636 da, bir eğrinin maksimum, minimum ve tanjantını bulmak için verdiği çabalar, Ş. Al-Tusi’den 5 asır sonra, onu da türevin keşfine götürmüştür. Artık matematik dünyası, yavaş da olsa, bunu anlayacak kadar olgundur. b) Analitik geometrinin ve kartezyen koordinat sistemini ortaya çıkması. R. Descartes’ın (1596-1650) geometriyi cebirleştirme çabaları ve bir eğriyi bir reper sisteminde çizme isteği analitik geometrinin doğmasına ve, bugün Descartes ‘a ithafen adlandırılan, “cartesien” koordinat sisteminin ortaya çıkmasına yol açacaktır. Ve, c) türev ile entegral arasındaki, bugün “Kalkülüsün Temel Teoremi” dediğimiz, ilişkinin Newton (1643-1727) ve Leibniz (1646-1716) tarafından, birbirinden bağımsız olarak, bulunmasıdır. Böylelikle “ Integral Calculus” doğacaktır. Bu da, o güne kadar kullanım alanı oldukça sınırlı olan matematiğin önünü açacak ve matematiği evrensel bir bilim konumuna getirecektir. Ayrıca, kalkülüsle beraber bilimsel fizik ve mühendislik bilimleri de doğacaktır. Türevden önce, differensiel denklem, dolaysıyla bilimsel fizik yoktu. Bir differensiyel denklem, fiziki bir olayın metematiki ifadesindir. Bu çalışmalar ve astronomideki gelişmeler matematiği başka bir düzeye, yeni bir döneme taşıyacaktır.
4- Klasik Matematik Dönemi
1700- 1900 yılları arasını kapsayan ve matematiğin altın çağı olarak bilinen, bu dördüncü dönem, klasik matematik dönemidir. 18. asırda matematiğe en önemli katkıları yapan bilim adamlarının başında Euler, Laplace, Lagrange ve D’Alembert’i sayabiliriz. Leonhard Euler (1707-1783) İsviçre’de, Basel de doğmuş, meslek hayatının tamamı Petersbourg ve Berlin’de geçmiştir. Tarihin en üretken bilim adamıdır. Kalkülüsün ortaya çıkardığı olanakları sayılar teorisinden, differensiyel denklemlere; differensiyel denklemlerden, mühendislik problemlerine… uygulayan Euler, 30.000 sayfadan fazla bilimsel eser üretmiştir. Öldükten 50 sene sonra dahi, birikmiş makalelerinin yayını sürmüştür. Euler’le matematik evrensel boyutlara erişmiştir. Bugün bile matematikçilerin yaptığı işlerin bir çoğunun temel fikri veya başlangıcı Euler’in çalışmalarıdır. Euler’le Analiz yeni bir bilim dalı olarak temeyyüz etmiştir; bu dalın büyük babaları Eudoxus ve Arşimed ise, babası Euler’dir. Laplace (1749-1827) Fransa’da, Normandia’ da doğmuştur.
Gök ve yer mekaniği hakkında yazdığı 11 ciltlik eseri, bütün zamanlarda mekanik hakkında yazılmış en kapsamlı eserlerinden biridir. “Theorie Analytique des Probabilites” başlıklı kitabı olasılık teorisinin ilk önemli eseridir. Joseph-Louis Lagrange (1736-1813) İtalya’da Turin’da doğmuş, meslek hayatının büyük bölümünü Berlin ve Paris’te geçirmiştir. İtalya’da doğmasına rağmen Fransız matematikçisi olarak bilinir. Lagrange cebirsel denklemlerin çözülebilirliği, mekanik, differensiyel denklemler ve varyasyon hesabına önemli katkılar yapmış, fikirleri ve yöntemleri bugün de kullanılan bir bilim adamıdır. Jean Le Rond D’Alembert (1717-1783) Paris’te doğmuş, Fransa’da yaşamıştır. D’Alembert kısmi differensiyel denklemleri ilk inceleyen bilim adamlarından biridir. Kısmi differensiyel denklemler ve akışkanlar mekaniği ilgili çalışmaları ve felsefi yazıları dışında, Diderot ile beraber editörlüğünü yaptığı ünlü 28 ciltlik “Encyclopedie” nin matematik maddelerinin hemen -hemen tümünü D’Alembert yazmıştır. Bu eser Fransız aydınlanmasının temel eserlerinden biridir.
. 1700- 1900 yılları arasını kapsayan ve matematiğin altın çağı olarak bilinen, bu dördüncü dönem, klasik matematik dönemidir. 18. asırda matematiğe en önemli katkıları yapan bilim adamlarının başında Euler, Laplace, Lagrange ve D’Alembert’i sayabiliriz. Leonhard Euler (1707-1783) İsviçre’de, Basel de doğmuş, meslek hayatının tamamı Petersbourg ve Berlin’de geçmiştir. Tarihin en üretken bilim adamıdır. Kalkülüsün ortaya çıkardığı olanakları sayılar teorisinden, differensiyel denklemlere; differensiyel denklemlerden, mühendislik problemlerine… uygulayan Euler, 30.000 sayfadan fazla bilimsel eser üretmiştir. Öldükten 50 sene sonra dahi, birikmiş makalelerinin yayını sürmüştür. Euler’le matematik evrensel boyutlara erişmiştir. Bugün bile matematikçilerin yaptığı işlerin bir çoğunun temel fikri veya başlangıcı Euler’in çalışmalarıdır. Euler’le Analiz yeni bir bilim dalı olarak temeyyüz etmiştir; bu dalın büyük babaları Eudoxus ve Arşimed ise, babası Euler’dir. Laplace (1749-1827) Fransa’da, Normandia’ da doğmuştur.
Gök ve yer mekaniği hakkında yazdığı 11 ciltlik eseri, bütün zamanlarda mekanik hakkında yazılmış en kapsamlı eserlerinden biridir. “Theorie Analytique des Probabilites” başlıklı kitabı olasılık teorisinin ilk önemli eseridir. Joseph-Louis Lagrange (1736-1813) İtalya’da Turin’da doğmuş, meslek hayatının büyük bölümünü Berlin ve Paris’te geçirmiştir. İtalya’da doğmasına rağmen Fransız matematikçisi olarak bilinir. Lagrange cebirsel denklemlerin çözülebilirliği, mekanik, differensiyel denklemler ve varyasyon hesabına önemli katkılar yapmış, fikirleri ve yöntemleri bugün de kullanılan bir bilim adamıdır. Jean Le Rond D’Alembert (1717-1783) Paris’te doğmuş, Fransa’da yaşamıştır. D’Alembert kısmi differensiyel denklemleri ilk inceleyen bilim adamlarından biridir. Kısmi differensiyel denklemler ve akışkanlar mekaniği ilgili çalışmaları ve felsefi yazıları dışında, Diderot ile beraber editörlüğünü yaptığı ünlü 28 ciltlik “Encyclopedie” nin matematik maddelerinin hemen -hemen tümünü D’Alembert yazmıştır. Bu eser Fransız aydınlanmasının temel eserlerinden biridir.
Bu yüzyılın matematiği çeşitli, kapsamlı ve fikir yönünden zengindir. En önemli zaafları, kesinlik (rigor) eksikliği; yapılan işlerin, günümüzün standartlarına göre, yarım-yamalak, kusurlu ve eksik oluşudur. Matematiğin o zamanda erişmiş olduğu düzeyde başka türlü olabilir miydi, bilmiyorum.
1800-1900 Arası. 19. asır çok sayıda, matematiğe önemli katkıları olmuş, bilim adamın yaşadığı bir asırdır. Bunların her birini teker -teker ele alıp, onların neler yaptığını anlatmak, bu konuşma çerçevesinde mümkün değildir; ayrıca, buna bilgim de yetmez. Bunun yerine, bu asırda matematik nereden nereye geldi sorusuna cevap vermeye çalışacağım. 1800 lerin başında matematik derin bir kriz içindeydi. Bunun nedeni, Fermat (1636) dan beri türevin tanımında, ve türevin işe karıştığı bir çok yerde, sonsuz küçük (infinitesimal) kavramının kullanılması ve matematikçilerin bunu çok tutarsız bir şekilde kullanmalarıydı. Bu tarihlerde henüz limit kavramının olmadığını ve türevin limit vasıtasıyla değil, “sonsuz küçük” kavramı kullanılarak tanımlandığını burada belirtmem gerekir. Bu tutarsızlık çok eleştirilmiş, özellikle de düşünür-din adamı G. Berkley (1685-1753) nin matematikçilerin tutarsızlığını ortaya koyduğu 40 sayfalık bir eleştiri kitabı derin etki yapmış, bir çok matematikçinin meslek değiştirmesine ve matematiğe karşı tavır almalarına neden olmuştur. 1800 başında, fonksiyon kavramının, son yüz yıldır kullanıla gelmesine karşın, henüz doğru-dölek tanımlanmamış olması ve matematikçilerin fonksiyonu aynı şekilde anlamamaları da başka bir anlaşmazlığın ve karmaşanın nedeniydi.
1800 lerin başında süreklilik ve fonksiyon serilerinin yakınsaklığı doğru-dölek anlaşılmamıştı; henüz düzgün süreklilik ve düzgün yakınsaklık kavramları ortada yoktu. Entegral kavramı türev kavramının tersi olarak görülüyordu; türevden bağımsız bir entegral ve entegrallenebilirlik kavramı yoktu. 1800 lerin başında, bugün matematiğin en önemli teorilerinden biri olan, kompleks fonksiyonlar teorisi henüz yoktu. Antik Yunan çağından kalma ve çok uğraşılan beş sorudan ( Bunların ilk dördü, geometrik çizim yaparak, 1) bir açıyı üç eşit parçaya bölmek. 2) Alanı verilen bir dairenin alanına eşit alanı olan bir kare bulmak. 3) Hacmi verilen bir küpün hacminin iki katına eşit hacmi olan bir küp bulmak; ve 4) bir dairenin içine, p sayısı asal olmak kaydı ile, hangi p ler için düzgün p-genler çizilebileceğini bulmak idi. 5. Soru, Öklid geometrisinin beşinci postulatı olan, “bir doğruya onun dışından bir ve yalnız bir paralel çizilebilir “ postulatının diğer dördünün sonucu olarak elde edilip-edilemeyeceği idi) hiç biri, 4 cü soru dışında ki o da Gauss tarafından daha yeni çözülmüştü, çözülememişti.
Cebirde, 5 ci dereceden polinomların köklerinin cebirsel ( köklü ifadelerle) çözülüp-çözülemeyeceği henüz bilinmiyordu. Cebir’in grup, halka, cisim, vektör uzayı gibi hiçbir yapısı henüz ortaya çıkmamıştı. Matris ve vectör kavramları henüz yoktu ( 2 li ve 3 lü determinantlar 1680 lerden beri biliniyor). Matematiksel fiziğin ana teoremleri henüz ortada yoktu; differensiyel geometri, topoloji gibi konular henüz doğmamıştı. 1800 lerin başında matematiğin durumu kısaca bu idi. 1820 lerde, A. Cauchy (1789-1855) limit kavramını, bugünkü kullandığımız şekliyle, tanımlayıp, türevi, sürekliliği ve, sürekli fonksiyonlar için, entegrali, limit kavramı yardımıyla tanımlaması, analizi, sonsuz küçük kavramından kaynaklanan krizden kurtarmış ve daha sağlam temeller üzerine oturtulmasını sağlamıştır. Cauchy’nin çalışmaları sonucu, kompleks fonksiyonlar teorisi doğmuş ve, Cauchy, B. Riemann (1820-1866) ve K. Weierstrass (1815-1884) gibi asrın büyük matematikçilerinin çalışmalarıyla, matematiğin en temel teorilerinden birine dönüşmüştür. G. Dirichlet’nin (1805-1859) 1830 larda fonksiyon kavramını bugün anladığımız manada tanımlaması matematiği başka bir kargaşadan kurtarmıştır.
Bu da özellikle Fourier serileri hakkında tartışmaları sona erdirecek, Fourier serileri ile ilgili çalışmaları tekrar başlatacaktır. Fourier serileri Analizin gelişmesinde en önemli rolü oynayan, bir bakıma modern matematiğin doğuşuna neden olan, gerek uygulamaları ve gerekse de matematikteki merkezi konumu açısından, matematiğin en önemli konularından biridir. Weierstrass ve öğrencilerinin çalışmaları sayesinde, 1850 lerden sonra, düzgün süreklilik, düzgün yakınsaklık gibi analizin vazgeçilmez kavramları ortaya çıkacak, fonksiyon serilerinin yakınsaklığı daha iyi anlaşılacaktır. F. Gauss’un (1777-1855) “ Cebir’in Temel Teoremi, ya da D’Alembert Teoremi” olarak bilinen teoremi ispatlaması bu asrın başka bir önemli olayıdır. Bu teorem bugün cisimler teorisinden spektral analize kadar bir çok teorinin temelinde olan bir teoremdir. Bütün zamanların en derin, en büyük bilim adamlarından biri olarak kabul edilen Gauss’un, sayılar teorisi, differensiel geometri, matematiksel fizik ve astronomiye katkıları bu asrın en önemli çalışmaları arasındadır. Bu asrın ve bütün zamanların en önemli matematikçilerinden biri olan Riemann kısa yaşamında, daha sonra her biri büyük bir teori olacak bir düzine konuyu başlatmış ya da onlara derin katkılar yapmış, matematiğe kavramsal bir bakış ve yaklaşım getirmiştir. Bunlardan bir kaçı: Riemann entegrali ve entegrallenebilirlik kavramı, Riemann yüzeyleri, Riemann geometrisi, differensiyel geometri, sayılar teorisi (Riemann hipotezi), kompleks analiz (Riemann yüzeyleri, Cauchy-Riemann denklemleri), cebirsel geometri, matematiksel fizik ve, daha sonraları topoloji ismini alacak olan, analysis situs tür. Yine bu asırda, yukarıda sözü edilen, antik Yunan çağından kalma 5 sorunun beşi de çözülmüştür.
1. ve 3. soruların mümkün olmadığı bir Fransız matematikçisi olan Wentzel tarafından 1837 de ispatlandı. 2. sorunun mümkün olmadığı, Lindemann’ın 1882 de pi sayısının tranzantal bir sayı olduğunun ispatından sonra anlaşıldı. 4. soru, yukarıda da söylendiği gibi Gauss tarafından 1796 da (p=17) için ve 1801 de de diğer p ler için tam olarak çözüldü. Cevap şudur: p bir asal sayı olsun. Verilen bir dairenin içine bir düzgün p-genin çizilebilmesi için gerek ve yeter koşul p nin p=2^n+1 ve n=2^k şeklinde olmasıdır. ( k=0 için, p=3 dür; k=1 için p=5, ve k=2 için p=17 dir). Bir dairenin içine düzgün bir beşgenin çizilebileceğini Öklid biliyordu; 7-gen çizilemeyeceğini Arşimed biliyordu. Arşimed’den 1800 yılları arasında geçen 2000 yılda bu soruda hiçbir ilerleme sağlanmamıştı; bu sorunun çözümü için Gauss’un dehası gerekiyordu. Öklid’ in 5. postulatına gelince, bu sorunun çözümü için insanların, “mantıki tutarlılık” ile “fiziki olurluluğun” aynı şey olmadığını anlamaları gerekiyordu. 5. postalatın yerine onun zıtları olan postulatlar koyarak, Öklid geometrisi kadar tutarlı, iki yeni geometri oluşturulabileceği Lobachevki (1792-1856), Bolyai (1802-1860), ve Riemann tarafından gösterildi. Cebir cephesine gelince, genç yaşta bu dünyadan ayrılan iki matematikçi, H. Abel (1802-1829) ve E. Galois (1811-1832) nın 5. dereceden polinomların cebirsel yöntemlerle köklerinin bulunup-bulunamayacağı konusunda çalışmaları sonucu grup teorisi doğdu. Kummer (1810-1893) ve öğrencilerinin Fermat’nın büyük teoremiyle ispatlamak için verdikleri uğraşı sonucu halka teorisi ve idealler teorisi; R. Dedekind (1831-1916) gerçel sayıların soyut bir tanımını vermek için yaptığı çalışmalar sonucu, cisim teorisi; Cayley (1821-1895 ) ve Sylvesterin (1814-1897 ) çok sayıda doğrusal denklemi tek bir denklem olarak göstermek ve çözmek için yaptıkları çalışmalar sonucu matris cebiri; ve Grassman (1809-1877 ) nın üç boyuttan çok boyuta geçme çabaları sonucunda da vectör uzayları doğdu. Bu kavramlar matematiğe yapısal (= stuructualist) yaklaşımı ve bakış açısını getirecektir.
Bu dönemi, 1700-1900 arasını, matematikte büyük ilerlemelerin olduğu, çok sayıda yeni teorinin doğduğu, yapısal değişikliklerin olduğu, ispatlarda kesinliğin ön plana çıktığı, kavramsal bakış açısının hesapsal yaklaşımın önüne geçtiği bir dönem, matematiğin altın çağı, olarak özetleyebiliriz.
Altın çağ bir krizle kapandı. Bu kriz yeni bir çağın doğum sancılarıydı. Bu çağ modern matematik çağıdır. Bundan sonraki kısımda, bu krizin nedenleri ne idi; modern matematik nedir, nasıl doğdu, ne yönde gelişti; bunları anlatmaya çalışacağım.
5-Modern Matematik Dönemi
Kümeler teorisinin, dolaysıyla, modern matematiğin, babası Georg Cantor (1845-1918) dır. G. Cantor Berlin üniversitesinde, Kummer’in ögrencisi olarak sayılar teorisinde tezini bitirdikten sonra, 1869 dan itibaren meslek hayatının sonuna kadar çalışacağı Halle üniversitesinde işe başlamıştır. Halle üniversitesinde çalışmaya başladığı yıllarda, o üniversitenin hocalarından, E. Heine’nın Cantor’a sorduğu bir soru Cantor’un yaşamını, matematiğin de seyrini değiştirecekti. Bu soru şu idi: Bir periodluk bir aralıkta, toplamı sıfır olan bir trigonometrik serinin katsayılarının hepsi sıfır mıdır? Cantor bu soruyla uğraşırken gerçel sayıların o güne kadar fark edilmeyen bir özelliğinin farkına varır. Bu da rasyonel sayılarla irrasyonel sayıların aynı çoklukta olmadığıdır. Başka bir ifadeyle, rasyonel sayıların kümesiyle irrasyonel sayıların kümesi arasında, her iki kümenin de sonsuz olmasına karşın, bire-bir bir dönüşüm yoktur. O halde bu iki kümenin sonsuzlukları aynı değildir. Böylelikle ortaya küme kavramı ve kümelerin, içerdikleri eleman çokluğu açısından, sınıflandırılması sorunu çıktı. Bu son kavram “sonsuzun” tek değil, çok olduğunu söylemektedir; bu da çok tepki çekecekti. Tarih boyunca, Elea’ lı Zeno’dan başlayarak, günümüze kadar, “sonsuz” insanları rahatsız etmiştir.
Aristo’dan Cantor’a kadar geçen zaman diliminde “sonsuz” anlayışı, temelde Aristo’nun görüşü olan, şu anlayıştır: Sonsuz, ufuk çizgisi gibi, var olmayan ama konuşma kolaylığı sağladığı için kullandığımız bir kavramdır. Bu kavramı “sınırsızlık” kavramı yerine kullanırız; bir şey, çoğalarak ya da büyüyerek, önceden belirleyeceğimiz bir çokluğun ya da büyüklüğün ötesine geçme potansiyeline sahipse, o şeye sonsuza gidiyor deriz. Başka bir deyimle, Aristo’nun sonsuz anlayışı “potansiyel sonsuz” anlayışıdır. Cantor’a göre ise “sonsuz” tek başına manalı bir söz değildir; manalı olan “sonsuz küme” kavramıdır; sonsuz kümeler ise var olan nesnelerdir. Burada “sonsuz küme” deyimi, büyükanne gibi, bölünmez bir terim olarak anlaşılmalıdır. O halde önce kümeler sonlu-sonsuz diye ikiye ayrılacak; sonra da sonsuz kümeler, kendi aralarında, sonsuzluklarına göre, çeşitli sınıflara ayrılacaktır. Böylelikle ortaya sayısız “sonsuz küme” sınıfları çıkacaktır. Bu da çok çeşitli “sonsuzluğun “ olduğu manasına gelmektedir. Cantor’un bu sonsuz anlayışı, Kronecker ve Poincaré gibi bir çok ünlü matematikçi tarafından tepki ile karşılandı. Bunun sonucu olarak ta, matematikçiler, “sonsuzu” Cantor gibi anlayanlar ve Aristo gibi anlayanlar olmak üzere, iki guruba ayrıldılar. Küme kavramının, aksiyomatik olarak tanımlanmaksızın, Cantor’un yaptığı gibi, sözlük manasında kullanılması, kümeler teorisini de çıkmaza soktu; “bütün kümelerin kümesi bir küme midir” gibi yeni paradoksları ortaya çıkardı. Bu da matematikçileri, kümeler teorisinden vazgeçilip-vazgeçilmemesi konusunda, ikinci bir kez böldü.
Üçüncü bir sorun da, bir matematiksel ispatın ne olduğu, geçerliliği, meşruluğu sorunuydu. Matematikte deney ya da gözlem olmadığı için, tartışma konusu olan bir ispat, teori veya teorem hakkında son sözü deneye, ya da gözleme bırakma olanağı yoktur. Bir matematikçi “ öyle bir x vardır ki…” dediği zaman var olduğunu iddia ettiği şeyi somut olarak ortaya koymak, en azından nasıl inşa edilebileceğini göstermek zorunda mıdır; yoksa, bir din adamının dini ilkelere dayanarak şeytanın varlığını ispatladığı gibi, bir matematikçinin de, aradığı şeyin nasıl elde edileceğini göstermeksizin, o şeyin var olduğunu, bir takım ilkelere dayanarak, ispatlaması yeterli midir?
- Kümeler teorisinin, dolaysıyla, modern matematiğin, babası Georg Cantor (1845-1918) dır. G. Cantor Berlin üniversitesinde, Kummer’in ögrencisi olarak sayılar teorisinde tezini bitirdikten sonra, 1869 dan itibaren meslek hayatının sonuna kadar çalışacağı Halle üniversitesinde işe başlamıştır. Halle üniversitesinde çalışmaya başladığı yıllarda, o üniversitenin hocalarından, E. Heine’nın Cantor’a sorduğu bir soru Cantor’un yaşamını, matematiğin de seyrini değiştirecekti.
Bu soru şu idi: Bir periodluk bir aralıkta, toplamı sıfır olan bir trigonometrik serinin katsayılarının hepsi sıfır mıdır? Cantor bu soruyla uğraşırken gerçel sayıların o güne kadar fark edilmeyen bir özelliğinin farkına varır. Bu da rasyonel sayılarla irrasyonel sayıların aynı çoklukta olmadığıdır. Başka bir ifadeyle, rasyonel sayıların kümesiyle irrasyonel sayıların kümesi arasında, her iki kümenin de sonsuz olmasına karşın, bire-bir bir dönüşüm yoktur. O halde bu iki kümenin sonsuzlukları aynı değildir. Böylelikle ortaya küme kavramı ve kümelerin, içerdikleri eleman çokluğu açısından, sınıflandırılması sorunu çıktı. Bu son kavram “sonsuzun” tek değil, çok olduğunu söylemektedir; bu da çok tepki çekecekti. Tarih boyunca, Elea’ lı Zeno’dan başlayarak, günümüze kadar, “sonsuz” insanları rahatsız etmiştir. Aristo’dan Cantor’a kadar geçen zaman diliminde “sonsuz” anlayışı, temelde Aristo’nun görüşü olan, şu anlayıştır: Sonsuz, ufuk çizgisi gibi, var olmayan ama konuşma kolaylığı sağladığı için kullandığımız bir kavramdır. Bu kavramı “sınırsızlık” kavramı yerine kullanırız; bir şey, çoğalarak ya da büyüyerek, önceden belirleyeceğimiz bir çokluğun ya da büyüklüğün ötesine geçme potansiyeline sahipse, o şeye sonsuza gidiyor deriz. Başka bir deyimle, Aristo’nun sonsuz anlayışı “potansiyel sonsuz” anlayışıdır. Cantor’a göre ise “sonsuz” tek başına manalı bir söz değildir; manalı olan “sonsuz küme” kavramıdır; sonsuz kümeler ise var olan nesnelerdir. Burada “sonsuz küme” deyimi, büyükanne gibi, bölünmez bir terim olarak anlaşılmalıdır. O halde önce kümeler sonlu-sonsuz diye ikiye ayrılacak; sonra da sonsuz kümeler, kendi aralarında, sonsuzluklarına göre, çeşitli sınıflara ayrılacaktır. Böylelikle ortaya sayısız “sonsuz küme” sınıfları çıkacaktır.
Bu da çok çeşitli “sonsuzluğun “ olduğu manasına gelmektedir. Cantor’un bu sonsuz anlayışı, Kronecker ve Poincaré gibi bir çok ünlü matematikçi tarafından tepki ile karşılandı. Bunun sonucu olarak ta, matematikçiler, “sonsuzu” Cantor gibi anlayanlar ve Aristo gibi anlayanlar olmak üzere, iki guruba ayrıldılar. Küme kavramının, aksiyomatik olarak tanımlanmaksızın, Cantor’un yaptığı gibi, sözlük manasında kullanılması, kümeler teorisini de çıkmaza soktu; “bütün kümelerin kümesi bir küme midir” gibi yeni paradoksları ortaya çıkardı. Bu da matematikçileri, kümeler teorisinden vazgeçilip-vazgeçilmemesi konusunda, ikinci bir kez böldü. Üçüncü bir sorun da, bir matematiksel ispatın ne olduğu, geçerliliği, meşruluğu sorunuydu. Matematikte deney ya da gözlem olmadığı için, tartışma konusu olan bir ispat, teori veya teorem hakkında son sözü deneye, ya da gözleme bırakma olanağı yoktur. Bir matematikçi “ öyle bir x vardır ki…” dediği zaman var olduğunu iddia ettiği şeyi somut olarak ortaya koymak, en azından nasıl inşa edilebileceğini göstermek zorunda mıdır; yoksa, bir din adamının dini ilkelere dayanarak şeytanın varlığını ispatladığı gibi, bir matematikçinin de, aradığı şeyin nasıl elde edileceğini göstermeksizin, o şeyin var olduğunu, bir takım ilkelere dayanarak, ispatlaması yeterli midir?
Prof. Dr. Ali Ülger
Kaynakça: http://home.ku.edu.tr/~aulger/histofmathematics.html

ATATÜRK VE MATEMATİK Atatürk’ ün yaşamında ilk olağan üstü başarısı çocukluk çağında, orta öğrenimi döneminde matematik dersinde olmuş ve bunun sonucu olarak dersin öğretmeni O’ nun adına “Kemal” adını vermiştir. Atatürk, Selanik Askeri Rüştiyesinde geçen bu olayla ilgili anısını şöyle anlatıyor: Atatürk’ün yaşamında matematiğin önemi bu güne kadar bildiğimiz veya ilkokullarda öğrenmiş olduğumuz gibi matematik öğretmeninin Kemal ismini vermesinden çok ötedir. Cumhuriyetten önce çeşitli okullarda okutulmuş matematik kitaplarını incelerseniz; içlerinde Arap harfleriyle yazılmış formüller; | |
 | |
| Atatürk’ ün matematik dünyasına kazandırdığı diğer bazı terimlerden de şöyle örnekler verebiliriz; | |
Bölen Bölme Bölüm Bölünebilme Çarpı Çarpan Çarpanlara Ayırma Çember Çıkarma Dikey Limit Ondalık Parabol Piramit Prizma Sadeleştirme Pay Payda Teğet | Maksumunaleyh Taksim Haric-i Kısmet Kabiliyet-i Taksim Zarb Mazrup Mazrubata Tefrik Muhit-i Daire Tarh Amudi Gaye Aşar’i Kat’ı Mükafti Ehram Menşur İhtisar Suret Mahrec Hatt-ı Mübas |
Atatürk’ ün bulduğu bu ve bunlar gibi bir çok terimler günümüzde hala geçerliliğini korumakta ve matematiği bizler için daha anlaşılır kılmaktadır. Atatürk’ ün amacı daima daha uyguna doğru ilerlemekti. Önerilen görüşleri haklı görünce hemen benimserdi. Atatürk’ ün ortaya koyduğu terimlerden bir takımı bugün kullanılırken bazıları çıkmış yerini daha uygunlara bırakmıştır. Örneğin; “tümey açı” yerine “tümler açı” , “bütey açı” yerine “bütünler açı” da olduğu gibi. Atatürk ilke adamı olduğu için bunları hoş görecek hatta sevinecekti. Yeter ki ortaya koyduğu ilke sarsılmasın yerine eski terimlere dönülmesin. Atatürk 1937 yılında yayınlanan bir geometri kitabı yazmıştır. Bu kitapta kullanılan yeni terimler ayrıntılarıyla açıklanmış ve üzerlerine örneklerde verilmiştir. Bu kitap geometri öğretenlere ve bu konuda bilgi edinmek isteyenlere kılavuz olarak kültür bakanlığınca yayınlanmıştır. A. Dilaçar anlatıyor: “1936 yılı sonbaharında bir gün Atatürk beni özel kalem müdürü Süreyya Demir’ in yanına katarak Beyoğlu’ndaki Haset Kitapevine gönderip uygun gördüğünüz Fransızca Geometri kitaplarından birer tane aldırdı. Bunları Atatürk’le beraber gözden geçirdikten sonra ben ayrıldım ve kış aylarında Atatürk bu eser üzerinde çalıştı. Geometri kitabı bu emeğin ürünüdür.” Mustafa Kemal bu geometri kitabını yazarak matematiğe daha anlaşılır yeni terimler kazandırmak isteğini Sivas’ ta girdiği bir geometri dersinde ortaya koymuştur. Atatürk sadece siyasi ve idari alandaki dehası ile değil, sayısal dünyadaki üstün başarısı ile de karşımıza çıkmış oluyor.
Atatürk'ün Geometri Kitabını İndir. 2349 kez indirildi.
ATATÜRK’ÜN GEOMETRİ KİTABI Bugün kullandigimiz “Matematik Terimleri”nin büyük bir çogunu Atatürk dilimize kazandirmis ve icat etmistir.
Atatürk'ün Geometri Kitabını İndir. 2349 kez indirildi. Virüs taraması yapıldı.
| |
“Ben öğrenim devrimde matematik konusuna çok önem vermişimdir ve bundan hayatımın çeşitli safhalarında başarı elde etmek için faydalanmış olduğumu söyleyebilirim. Onun için herkes matematik bilgisinin çok gerekli olduğuna inanmalıdır.” Mustafa Kemal Atatürk
ATATÜRK ve MATEMATİK
Atatürk, Türk Kurtuluş Savaşı’yla birlikte başlattığı eğitim ve bilim savaşını son nefesine kadar başarıyla devam ettirmiştir. Ulu Önder’in eğitim ve bilim alanında gerçekleştirdiği atılımlarla çok büyük başarılara ulaşılmıştır. Bu atılım hareketlerinden önceliği alan bilimlerden bir tanesi de matematiktir. Atatürk bu bilim alanında terimler türetmiş, kitap yazmış, gençlerin bu bilim alanında çalışmalarına bizzat öncülük yapmıştır.
Matematik; dil, ırk, din ve ülke tanımadan uygarlıklara zenginleşerek geçen sağlam, kullanışlı evrensel bir dildir. Birey için, toplum için, bilim için, teknoloji için vazgeçilmez değerdedir. Yayılma alanına ve derinliğine sınır konamayan bir bilimdir, bir sanattır.
Eski Yunanca matesis kelimesi matematik kelimesinin köküdür ve ben bilirim anlamına gelmektedir.
Daha sonradan sırasıyla bilim, bilgi ve öğrenme gibi anlamlara gelen máthema sözcüğünden türemiştir.
Mathematikós öğrenmekten hoşlanan anlamına gelir.
Osmanlı Türkçesinde ise matematiğe Riyaziye denilmiştir.
Matematik sözcüğü Türkçeye Fransızca mathématique sözcüğünden gelmiştir.
Atatürk’ün dil alanında yaptığı çalışmalar Türk eğitim ve bilim alanında yepyeni ufuklar açmış, eğitimin ve bilimin tüm topluma yayılmasında mihenk taşı oluştur. O Yeni Türk Alfabesiyle başlattığı devrimi her alanda devam ettirmiş ve Türk dilini her platformda geliştirmeyi hedef edinmiştir. Türkçe ile eğitim olmak üzere gerçekleştirdiği devrimlere bakıldığında Atatürk bilim alanındaki çalışmaları gerçekten övülmeye değerdir. Bu çalışmalardan matematik bilimi de hakkına düşeni almıştır.
Matematik adını nasıl almış ve riyaziye, bakın nasıl matematik olmuştur.
Türk Dili Kurultayı Komisyonlarında bir an;
Gazi, artık en büyük önemi terim komisyonlarına veriyordu. Bu komisyonlar ellerinden geldiği kadar cep kılavuzundan, taramalardan, derlemelerden, Divandan... Ve başka kaynaklardan araç alıp şaşılacak ölçüde çok terim uyduruyorlardı.
Gazi bu çalışma biçimini durduracak hiçbir emir vermedi. Ancak akşamları, konuşarak, komisyonlara sağlam prensipler aşılamaya bakıyordu:
• Doğu (İslam-Arap) kültürünün terimleri atılacak! Batı terimlerinin Türkçe karşılıkları aranacak.
• Bulunacak Türkçe karşılık Batı teriminin kavramını anlatabilmelidir. Karşılık, terimin kavramını anlatmıyorsa alınmayacak.
• Batı terimi Türk fonetiğine uygun imla (ortografi) ile millileştirilip alınacak; bu terim artık Türkçe sayılarak ortaokul ve lise öğretiminde kullanılacak.
Gazi bütün komisyonların hazırladığı uzun listeleri gözden geçiremezdi; buna vakti yoktu. Yalnız riyaziye (matematik) komisyonunun terimlerini kendi kontrolü altına almış, birer birer tartışmasını yaptırarak alınacak terimleri, Türk imlasıyla tespite çalışmıştı.
İlk terim riyaziye kelimesi idi. Komisyonun listesinde bu terime bir karşılık bulunmamıştı. Tartışma başladı:
Gazi: "Riyaziye nerden gelir, anlamı nedir?"
Komisyon Başkanı: "Efendim, riyazat'tan gelir, sofuların sıkı perhizi demektir."
Gazi: "Bunun Batı terimi nedir?"
Komisyon Başkanı: "Fransızcası mathematique, İngilizcesi mathematics, Almancası mathematik'tir, efendim."
Gazi: "Anlamı nedir?"
Komisyon başkanı: "Sayılabilen, ölçülebilen şeylerin sayılması, ölçülmesi yollarını araştıran birimler demektir."
Gazi: "Burada sofuların, perhizlerin işi yoktur. Bu terimin Türkçesi matematik'tir, efendim."
Terim, böyle bir tartışmadan sonra, matematik olarak alınmıştır.1
Matematik, insanın doğru düşünmesini, analiz ve sentez yapabilmesini sağlar. Bu ise başarının anahtarıdır.
Atatürk'ün yaşamında ilk olağanüstü başarısı, 1893 yılında, çocukluk çağında, orta öğrenimi döneminde matematik dersinde olmuş ve bunun sonucu olarak dersin öğretmeni Yüzbaşı Mustafa Bey2 O'nun adına "Kemal" ismini eklemiştir. Atatürk, Selanik Askeri Rüştiyesi'nde geçen bu olayla ilgili anısını şöyle anlatıyor :
" ... Rüştiyede en çok matematiğe merak sardım. Az zamanda bize bu dersi veren öğretmen kadar belki de daha fazla bilgi edindim. Derslerin üstündeki sorularla uğraşıyordum, yazılı sorular düzenliyordum. Matematik öğretmeni de yazılı olarak cevap veriyordu. Öğretmenimin ismi Mustafa idi, bir gün bana dedi ki:
- 'Oğlum senin de ismin Mustafa benim de. Bu, böyle olmayacak, arada bir fark bulunmalı. Bundan sonra adın "Mustafa Kemal" olsun. O zamandan beri ismim gerçekten Mustafa Kemal oldu.”
Atatürk'ün hayatını incelediğimizde karşımıza şöyle bir tablo çıkar. Emperyalizme karşı açılan ve kazanılan Ulusal Kurtuluş Savaşı, Yeni Türkiye Devleti’nin kurulması ve ardından yapılan Türk Devrimleri. Kısacası modern bir ülke yaratmak uğruna yaşanan bir hayat. Atatürk bu elli yedi yıllık yaşamında birçok başarıya ve ilke imza atmayı başarmıştır. Sanırım bunun sırrı, matematiksel zekasında gizliydi. Yani yapacağı her işi önceden planlayıp, zamanında ve yerinde yapmasındaydı.
Atatürk’ün matematikle ne ölçüde uğraştığını, Türk Dil Kurum Başuzmanı Agop Dilaçar'ın3 10.11.1971 tarihli bir yazısında görüyoruz.
Agop Dilaçar anlatıyor:
"Geometri kitabını Atatürk, ölümünden bir buçuk yıl kadar önce Üçüncü Türk Dil Kurultayı’ndan hemen sonra 1936-1937 yılı kış aylarında Dolmabahçe Sarayı’nda kendi eliyle yazmıştır.
1936 Sonbaharında bir gün Atatürk beni, Özel Kalem Müdürü Süreyya Anderiman’ın yanına katarak Beyoğlu’ndaki Haşet Kitabevi’ne gönderip uygun gördüğümüz Fransızca Geometri kitaplarından bir tane aldırttı. Bunlar Atatürk’le birlikte gözden geçirildikten sonra, yazılacak Geometri kitabının genel tasarısı çizildi. Bir süre sonra ben ayrıldım ve kış aylarında Atatürk bu eser üzerinde çalıştı. Geometri kitabı bu emeğin ürünüdür.”4
Atatürk, bunu, birtakım Fransızca geometri kitaplarını okuduktan sonra hazırlamış ve yapıt ilk kez 1937 yılında "Geometri öğretenlerle, bu konuda kitap yazacaklara kılavuz olarak Kültür Bakanlığınca yayınlanmıştır"5
Bu 44 sayfalık yapıttaki üçgen, dörtgen, beşgen, köşegen, eşkenar, ikizkenar, paralelkenar, yanal, yamuk, uzay, yüzey, düzey, çap, yarıçap, kesek kesit, yay, çember, teğet, açı, açıortay, içters açı, dışters açı, taban, eğik, boyut, kırık, çekül, yatay, düşey, yöndeş, konum, artı, eksi, çarp, bölü, eşit, toplam, oran, orantı, türev, alan, varsayı, gerekçe gibi terimler Atatürk tarafından türetilmiştir.
Atatürk’ün dil çalışmalarını yakından izleme olanağı bulan tanınmış dil uzmanı Agop Dilaçar, Atatürk’ün yazdığı geometri kitabı üzerine şunları söylüyor:
“Atatürk hep matematikle uğraşırdı. Eski geometri terimleri çok ağdalı idi. Ben bile uzun uzun bu terimleri okuduğum halde, şimdikiler karşısında güçlüğünü daha iyi anlıyorum. Pedagojide bir gerçek var: Fikir yolunun açık olması, bir ipucunun bulunması lazımdır. Yoksa bir külçe gibi çöker. Müselles kelimesini ele alalım. Arapça okullarımızdan kaldırılmıştır. Sülüs’ten müstak (türetilmiş) bir kelime olduğunu öğrenici nasıl bilsin? Arapça yoğurucu bir dildir. Örneğin müsteşrik, şark kelimesinden gelmiş bir kelimedir. Önüne, ortasına, arkasına birtakım heceler eklenmiş. Bunun aslını bulmak bir Arapça gramer meselesidir. Okullarımızdan Arapça, Farsça kaldırılmış olduğundan, öğrenici “müselles”i kütle kelime olarak karşısında görecektir. “Üç” aklına gelmeyecektir. Ama müselles yerine üçgen dersek, bir üç var “Gen”, Atatürk’e göre “genişlik”ten alınmıştır. Bir ipucu var “Dörtgen”, dörtten gelmiştir. Bir ipucu vardır Eşit, denk anlamına gelen eş’ten gelmiştir. Ama müsavi Arapça bir kelimedir. Bu sebeple Atatürk’ün prensipleri burada da doğru idi. Onun için bu en ağdalı olan bilim dalını ele aldı ve kitabı örnek olarak bıraktı.”
Atatürk terim çalışmalarının ülkedeki etkilerini, fiili olarak da inceledi. Ülkedeki pek çok okulu ziyaret ederek öncelikle matematik derslerine girdi ve öğrencilerin dersteki başarılarını gözlemledi. 1937 yılında Kültür Bakanı Saffet Arıkan, İçişleri Bakanı Şükrü Kaya, Sabiha Gökçen, İsmail Hakkı Tekçe ve yaveri Naşit Mengü eşliğinde bir heyetle Sivas Lisesi’ne gitmişti lisenin 9-A sınıfında programdaki geometri (o zaman ki adıyla hendese) dersine girmiş bu derste bir kız öğrenciyi tahtaya kaldırmıştı. Öğrenci, tahtada çizdiği koşut iki çizginin, başka iki koşut çizgiyle kesişmesinden oluşan açıların Arapça adlarını söylemekte zorluk çekip yanlışlıklar yapınca durumdan etkilenen Atatürk tepki gösterdi. “Bu anlaşılmaz Arapça terimlerle, öğrencilere bilgi verilemez. Dersler, Türkçe yeni terimlerle anlatılmalıdır” diyerek tebeşiri eline aldı, tahtada çizimlerle ‘zaviye’nin karşılığı olarak ‘açı’, ‘dılı’nın karşılığı olarak ‘kenar’, ‘müselles’in karşılığı olarak ‘üçgen’ gibi Türkçe yeni terimleri kullanarak, birtakım geometri konularını bu arada Pisagor teoremini anlattı.6
_%201%20(2)(1).jpg)
_%203a(2).png)
Atatürk Sivas Lisesi'nde 9-A sınıfında geometri dersinde. (13 Kasım 1937)
Atatürk matematiğin hayatındaki yeri ve önemini şu sözlerle anlatmaktadır. “Ben öğrenim devrimde matematik konusuna çok önem vermişimdir ve bundan hayatımın çeşitli safhalarında başarı elde etmek için faydalanmış olduğumu söyleyebilirim. Onun için herkes matematik bilgisinin çok gerekli olduğuna inanmalıdır.”
Atatürk’ün matematiğe olan tutkusunu ve sayısal dünyaya olan yatkınlığını O'nun yaşamı boyunca kazandığı zaferlerin mayasında görmek mümkündür.
Dr. Tuna Yılmaz
1. Ahmet Cevat Emre, İki Neslin Tarihi, sayfa: 339-340
2. Yüzbaşı Mustafa Bey: Atatürk’ün, Selanik Askerî Rüştiyesinde Matematik öğretmenidir. Öğrencisinin yeteneklerini sezip O’na Kemal adını takmıştır. Bu şekilde O’nun kendisinden ve arkadaşlarından farklı ve üstün durumunu tesbit etmiş, O’na, daha iyiye, daha güzele doğru gitmek için sürekli bir teşvik nedeni sağlamıştır.
3. Mustafa Kemal Atatürk'ün Türkçe ile ilgili çalışmalarına verdiği katkılardan dolayı "Dilaçar" soyadını almıştır.
4. Agop Dilâçar, “Geometri” kitabının “Önsöz”ü, Türk Dil Kurumu Yayını, 1981, sayfa:5
5. Geometri, Türk Dil Kurumu Yayınları / Atatürk Dizisi: 4.Türk Tarih Kurumu Basımevi, Ankara, 1971, sayfa:5-7, I.
6. Ömer L. Örnekol’un Anıları, Bilim ve Teknik Dergisi, Kasım 1982, sayı: 180
Kastamonu Matematik | www.kastamonumatematik.com
Kastamonu Matematik | www.kastamonumatematik.com
Kartezyen koordinat sistemi, iki sayı doğrusunun sıfır noktasında birbiri ile dik kesişmesi sonucu oluşur. Yatay eksen “x ekseni (apsisler ekseni)”, dikey eksen ise “y ekseni (ordinatlar ekseni)” olarak isimlendirilir.
Koordinat eksenlerinin kesim noktası ise “başlangıç noktası” veya “orijin” olarak adlandırılır.
Kartezyen koordinat sistemindeki herhangi bir nokta sıralı ikililerle belirlenir ve her noktaya karşılık gelen bir sıralı ikili vardır.

Kastamonu Matematik | www.kastamonumatematik.com
Kastamonu Matematik | www.kastamonumatematik.com
Dörtgenler (video)
1-) ParalelKenar Dörtgen
Karşılıklı kenarları eşit ve paralel olan dörtgenlere paralelkenar denir.
[AB] // [DC]
[AD] // [BC]
|AB| = |DC|
|AD| = |BC|
Paralelkenarda karşılıklı açılar eş, komşu açılar bütünlerdir.
|AE| = |EC|
|DE| = |EB|
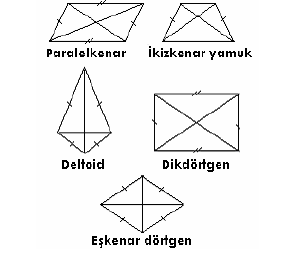
2-) Eşkenar Dörtgen;
-Dört kenarı birbirine eşit olan paralelkenara eşkenar dörtgen denir.
-Paralelkenar için geçerli olan bütün özellikler eşkenar dörtgen için de geçerlidir.
-Bütün kenar uzunlukları eşit olduğundan, alanı;A(ABCD)=a.h (bir kenar uzunluğunun yükseklikle çarpımı.)
-Eşkenar dörtgende köşegenler birbirini dik keser.
-Eşkenar dörtgenin köşegenleri aynı zamanda açıortay doğrularıdır.
3-) Kare;
-Bütün kenar uzunlukları eşit ve bütün açıları 90° olan dörtgene kare denir.
-Bir kenar uzunluğu a olan karenin alanı;A(ABCD)=a2 dir.
-Karenin köşegenleri birbirini dik ortalar. Köşegenlerin kenarlarla yaptığı açılar 45° dir.
-Karenin çevresi=4a
4-) Dikdörtgen;
-Karşılıklı kenar uzunlukları eşit ve bütün açıları 90° olan dörtgene dikdörtgen denir.
-Dikdörtgen paralelkenarın açıları 90° olan halidir. Bu nedenle paralelkenarın sahip olduğu bütün özelliklere sahiptir.
-Dikdörtgenin alanı farklı iki kenarının çarpımına eşittir. A(ABCD) = a.b
-Dikdörtgenin çevresi =2a+2b.
-Dikdörtgende köşegen uzunlukları eşittir. Köşegenler birbirlerini ortalar.
Yamuk
Yalnız iki kenarı paralel olan dörtgene, yamuk denir.
Yamuğun paralel olan kenarlarına, yamuğun tabanları, parelel olmayan kenarlarına yanal kenarlar denir.
Yamuğun, yanal kenarları üzerindeki açılar bütünlerdir. m(A) + m(D) = 180° , m(B) + m(C) = 180°
Yan kenarların orta noktalarını birleştiren doğru parçasına, orta taban denir. Orta taban uzunluğu, alt ve üst tabanlarının uzunluklarının toplamının yarısı kadardır.
Beşgen
5 kenarı ve 5 köşesi olan çokgen beşgendir.
Besgenlerin iç açıları toplamı 540°, dış açıların toplamı ise 360°'dir.
Kosegen sayisi n(n-3)/2 formuluyle bulunur. n kenar sayisini belirtir.
Altıgen
Altıgen altı köşesi,altı açısı ve altı kenarı olan bir çokgendir.
Dış açıları toplamı 360 derecedir.
Düzgün altıgen tüm açıları eş ve tüm kenar uzunlukları birbirine eş olan çokgendir.
Düzgün altıgen birbirine eş 6 adet eşkenar üçgenden oluşur.
Düzgün altıgenin bir iç açısı 120 derece olup, bir dış açısı da 60 derecedir.
Kastamonu Matematik | www.kastamonumatematik.com
ÇEMBER (video)
Çember, sabit bir noktadan eşit uzaklıkta bulunan noktaların meydana getirdiği bir şekildir.Yüzük,simit gibi.Çemberi çizerken pergelle saat yönü veya saat yönünün tersi doğrultusunda hareket ettirilerek çizimi yapılır.
Çemberin Elemanları:
Çemberin iki noktası arasında kalan parçasına çember yayı, çember parçası yada yay denir.
Bir çemberin üzerindeki iki noktadan geçen doğruya kesen denir.
Bir kesenin çember içinde kalan parçasına kiriş denir.
Merkezden geçen kirişe çap denir.Bir çemberdeki en büyük kiriş çaptır.
Çemberde iç bölge,dış bölge ve çemberin üzeri vardır.
Noktalarla Çemberin Durumları:
Doğrularla Çemberin Durumları:
Çemberde Açılar ve Yaylar
Merkez Açı: Köşesi merkezde olan açıya merkez açı denir.Merkez açının iç bölgesinde kalan çember parçasına merkez açının gördüğü yay denir.Merkez açı gördüğü yayın ölçüsüne eşittir.Merkez açının ölçüsü genelde 0 derece ile 180 derece arasında olur.
Çevre Açı: Köşesi çember üzerinde olan açıya çevre açı denir.Çevre açının iç bölgesinde kalan çember parçasına çevre açının gördüğü yay denir.Çevre açı gördüğü yayın yarısına eşittir. Çevre açının ölçüsü genelde 0 derece ile 360 derece arasında olur.
Majör (büyük) Çember Yayı: Merkez açının kenarlarının çemberi veya daireyi kestiği noktaların arasındaki yaylardan büyük olana majör çember yayı denir.
Minör (küçük) Çember Yayı: Merkez açının kenarlarının çemberi veya daireyi kestiği noktaların arasındaki yaylardan küçük olana minör çember yayı denir.Merkez açının ölçüsü minör yayın ölçüsüne eşittir.
Minör yayın ölçüsünü belirledikten sonra, bu ölçüyü 360 dereceden çıkartarak majör yayı buluruz.Birini bulursak diğerini bulmak için 360 dereceden çıkartırız.
Yarım Çember: Merkez açı, doğru açı ise yani 180 derece ise gördüğü yaya yarım çember yayı kısaca yarım çember denir.
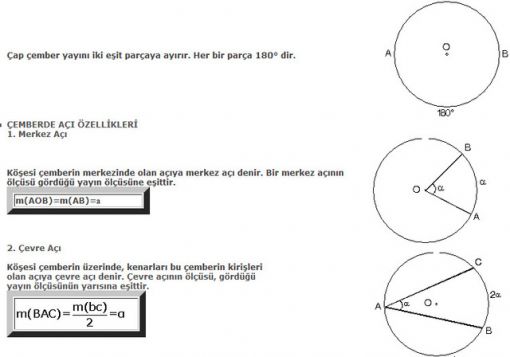
Kastamonu Matematik | www.kastamonumatematik.com
Bilinçli tüketim aritmetiği yüzde faiz hesapları problemleri (video)

Kastamonu Matematik | www.kastamonumatematik.com
ÜSLÜ SAYILAR (video)
Üslü sayı, bir doğal sayının kendisi ile çarpımlarının kısa şekilde gösterilmesidir.




 |
 |
 |
 |
 |
 |
 |
 Sıfır dışındaki tüm sayıların sıfırıncı kuvveti (+1) dir. Sıfır dışındaki tüm sayıların sıfırıncı kuvveti (+1) dir. |
 |
 ve ve  hariç üslü doğal sayılarda üs ile taban yer değiştirilirse sayının değeri de değişir. hariç üslü doğal sayılarda üs ile taban yer değiştirilirse sayının değeri de değişir. |
 |
Negatif sayıların üstleri alınırken, üs parantez üstünde ise hem sayıyı hem işareti etkiler, işareti sayıyı etkilemez.
7. sınıf faktöriyel permütasyon olasılık (video)
Kastamonu Matematik | www.kastamonumatematik.com




Kastamonu Matematik | www.kastamonumatematik.com


Dönme simetrisi nedir?
Bir şekil, bir nokta etrafında döndürüldüğünde, o nokta dönme hareketinin merkezi olur. Dönme simetrisi verilen şeklin bir nokta etrafında sağa, sola döndürülmesidir. Şeklin biçimi ve boyutu değişmez, sadece şeklin yönü değişebilir.
Bir şekil kendi merkezi etrafında döndürüldüğünde 360 dereceden küçük açılı dönmelerde en az bir defa kendisi ile çakışıyorsa bu şekil dönme simetrisine sahiptir. Kare 90 derece,180 derece,270 derece döndürüldüğünde yine kendisi ile çakıştığından dönme simetrisi vardır. Ama düzgün olmayan bir beşgen sadece 360 derece döndüğünde kendisi ile çakışır. Bu yüzden düzgün olmayan beşgen dönme simetrisine sahip değildir.
180 derecelik dönme(yarım dönme), merkezi dönme veya noktaya göre simetri olarak adlandırılır.
360 derecelik dönme, en az bir kez kendisiyle çakışması yani üst üste gelmesidir.
90 derecelik dönme çeyrek dönmedir.
Dönme simetrisinde verilen geometrik şeklin en küçük dönme simetri açısı bulunurken; verilen şeklin tam ortasına dönme merkezi işaretlenir. Verilen geometrik şeklin kaç eşit kenarı varsa yada kaç tane birbirine eşit farklı yönlü yüzü varsa dönme simetri sayısı budur. Ve 360 derece bu kenar sayısına bölünerek en küçük dönme simetri açısı bulunur. Yani dönme simetri sayısı kenar sayısına eşit olacak. Ama kenarları birbirine eşit düzgün çokgen tarzındaki şekiller için.
Örneğin; Karenin en küçük dönme simetri açısı 360:4=90 derece,
düzgün altıgenin en küçük dönme simetri açısı 360:6=60 derece
eşkenar üçgenin en küçük dönme simetri açısı 360:3=120 derecedir.
Buradan anlaşıldığı üzere düzgün çokgenler yani eşkenar üçgen,kare,düzgün altıgen,düzgün beşgen dönme simetrisine sahiptir ve en küçük dönme simetri açısı vardır.
Yatay ve dikey simetri nedir?
Yatay simetrisi denilirse şeklin ortasından ama yatay olarak simetri doğrusunu geçirecez. Alt ve üstte aynısı varsa yatay simetrisi vardır.
Dikey simetrisi denilirse şeklin ortasından ama dikey olarak simetri doğrusunu geçirecez. Sağ ve solda aynısı varsa dikey simetrisi vardır.
Öteleme simetrisi ve doğru simetrisi nedir?
Şeklin kendisi ve öteleme sonundaki görüntüsü eş ve simetriktir. Bu tür simetriye öteleme simetrisi denir.
Şeklin verilen bir doğruya yansıması yani simetrisi alınırsa buna doğruya göre simetri denir.
Aradaki fark; öteleme simetrisinde aynı şekil belirli birim yol alarak yer değiştirmiş yön değişmemiştir. Ama doğru simetrisinde şeklimiz simetri doğrusuna göre katlanmış aynı şekil yan tarafa çıkmış ve yön değiştirmiştir.

Türk Bayrağının çizimi (video)
29 Mayıs 1936 tarihinde “Türk Bayrağı Kanunu” kabul edilmiştir. Daha sonra bu kanunun yerini 24 Eylül 1983 tarihinde Resmi Gazete’de yayımlanan “Türk Bayrağı Kanunu” almıştır. Kanun, Türkiye’de kullanılan bütün bayrakların en ve boy oranını, rengini, ay ile yıldızın yerini, boyutlarını ve her türlü özelliklerini belirtmektedir. Türk bayrağı, bayrak kanununda ifade edildiği hâliyle kesin şeklini almıştır. Aşağıda çizimi verilen Türk bayrağını inceleyiniz.
Bayrağın direk tarafına gelen kenarlarına uçkurluk denir. Bayrak çiziminde temel ölçü genişliktir. Genişlik, G ile gösterilir. Diğer ölçüler genişliğe göre hesaplanır. Bayrağımızın çizimine ait ölçüler aşağıdaki tabloda verilmiştir.

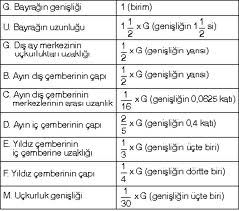
Kastamonu Matematik | www.kastamonumatematik.com









Kastamonu Matematik | www.kastamonumatematik.com
 Çokgenlerin Özellikleri, İç açıları toplamı (video)
Çokgenlerin Özellikleri, İç açıları toplamı (video)
Çokgenlerin kenarlarından geçen doğrular çokgenlerin iç bölgelerinden de geçiyorsa bu çokgenler içbükey, geçmiyorsa dış bükey çokgenler olarak adlandırılır.
Bir çokgenin ardışık iki kenarının oluşturduğu açılara çokgenin iç açıları, aynı köşeden geçen bir kenarın uzantısıyla ardışık kenarlann oluşturduğu açılara da çokgenin dış açıları denir.
Bir çokgenin bir köşesindeki iç ve dış açılannm ölçüleri toplamı 180° olduğundan bu açılar bütünlerdir.
Bir çokgenin ardışık olmayan iki köşesini birleştiren her doğru parçasma çokgenin bir köşegeni denir.
n tane kenarı olan bir çokgenin iç açılarının ölçüleri toplamı, (n-2)x180 bağıntısı ile bulunur.
n tane kenarı olan bir düzgün çokgenin bir iç açısının ölçüsü (n-2)x180 / n bağıntısı ile bulunur.
n tane kenarı olan bir çokgenin dış açılarının ölçüleri toplamı her zaman 3600 dır.
; n tane kenarı olan bir düzgün çokgenin bir dış açısının ölçüsü 360 / n bağıntısı ile bulunur.

Kastamonu Matematik | www.kastamonumatematik.com
BİR BİLİNMEYENLİ DENKLEMLER (video)
İçerisinde eşitlik ve bir bilinmeyen bulunan ifadelere bir bilinmeyenli denklemler denir. (2x+6=0) Buradaki bilinmeyen yerine değişken de kullanılabilir.Denklemi doğru yapan değişkenin veya bilinmeyenin değerine denklemin çözümü, bu doğru değeri bulma işlemine denklemi çözme denir.Diğer bir deyişle denklemi sağlayan bilinmeyene denklemin kökü,denklemin köklerinden oluşan kümeye denklemin çözüm kümesi denir.
Denklemi çözerken:
11) Bir sayının 5 eksiği
Çözüm :
‘Bir sayının’ , hangi sayı olduğu bilinmediği için , ‘bir sayıyı’ temsil eden bir değişken seçilir.Bu değişken herhangi bir sembol veya harf olabilir.’a’ harfi ‘bir sayıyı’ temsil eden değişken olarak seçerek ‘bir sayının 5 eksiği’
a-5 cebirsel ifadesiyle gösterilir.
Buna göre ; örneğin sayı 78 ise 5 eksiği a-5 = 78-5=73,
Sayı 34 ise 5 eksiği a-5 = 34-5=29 olur.
Çözüm :
Ebru’nun yaşını ‘y’ ile gösterirsek , Ebru’nun yaşının 5 katı 5y ile gösterilir. Ebru’nun yaşının 5 katının 2 eksiği ise 5y-2 şeklinde gösterilir.
13) 3,6,9,12… sayı örüntüsüne göre ;
Örüntünün 5 ve 6. adımlarında ki sayıları bulalım.
Çözüm :
Örüntüyü incelediğimizde her bir adımda ki sayının , adım sayısının 3 katına eşit olduğu görülmektedir.Buna göre ;
5. Adımda ki sayı 3.5=15
6.Adımda ki sayı 3.6=18 olacaktır.
Not: ‘n’ harfi verilen örüntüdeki sayıların sırasını veya yerini belirten bir işaret veya semboldür.Bu yüzden ‘n’, örüntünün ‘n.sayısı’ , ‘temsilci sayısı’ veya ‘genel sayısı’ olarak adlandırılır.
14) Bir sayının 9 fazlası ifadesine karşılık gelen cebirsel ifadeyi yazalım.
Çözüm :
Bir sayı ‘b’ olsun . Bu sayının 9 fazlasını istiyor. Bu şekilde cebirsel ifade : b+9 olur.
15) Bir sayının 3 katının 17 fazlası ifadesine karşılık gelen cebirsel ifadeyi yazalım.
Çözüm :
Bir sayı ‘x’ olsun . Bu sayının 3 katını istiyor .Bu durum da cebirsel ifade 3x olur.Bir sayının 3 katının 17 fazlası dediği için bu cebirsel ifadeye ‘+
16) ‘Arzu Burak’dan 6 yaş küçüktür.’ İfadesinde Burak’ın yaşı bilinmediğinden ‘y’ ile temsil edilir.Arzu’nun yaşı ‘y-
17) 2 , 4 , 6 , 8 … örüntüsüne karşılık gelen cebirsel ifadeyi yazalım.
Çözüm :
Cebirsel ifade : 2n ‘dir.
18) 3 , 7 , 11 , 15 sayı örüntüsünde karşılık gelen cebirsel ifadeyi değişken kullanarak yazalım.
Çözüm :
Cebirsel ifade : ‘4n-
19) 0 , 3 , 6 , 9 … örüntüsüne karşılık gelen cebirsel ifadeyi bulalım.
A) 3n B)n+3 C) 6n-3 D) 3n-3
Çözüm:
Böyle sorularda verilen sayıların cebirsel ifadesi bulunur. Bulunamazsada örüntü deki sayılar şıklardaki ‘n’ (yani bilinmeyen) yerine konularak sorular çözülür.Cevap ‘’3n-3’’ olarak yazılır . Yani ‘D’ şıkkı .
20) 5ab-7b+4a cebirsel ifadesindeki terim sayısını, bilinmeyenleri, katsayıları, katsayılar toplamını bulalım.
Çözüm:
Terimleri 5ab, -7b , 4a 'dır.
Bilinmeyenleri a ve b 'dir.
Katsayıları 5, -7 , 4 'tür.
Katsayılar toplamı 5-7+4= 2 'dir.
Çözüm:
4x-7 = 4.10-7 = 40-7 = 33 olur.
22) 'Bir sayının 12 fazlasının 2 katı' cümlesinin cebirsel ifadesini yazalım.
Çözüm:
(a+12).2
23) 'Bir sayının 2 katının 12 fazlası' cümlesinin cebirsel ifadesini yazalım.
Çözüm:
2a+12
24) 'Bir sayının 3 eksiğinin 3 katının yarısı' cümlesinin cebirsel ifadesini yazalım.
Çözüm:
(x-3).3 / 2
25) Bir sayının 5 eksiğinin yarısı 34'tür.Cebirsel ifadesindeki bilinmeyen sayıyı bulalım.
Çözüm:
x-5 / 2 = 34 cebirsel ifadeyi yazdıktan sonra payda durumundaki 2'yi 34'ün yanına çarpım olarak atarız.
x-5 = 34.2
x-5 = 68 şimdi de -5'i 68'in yanına +5 olarak atarız.
x = 68+5
x = 73
26) Aşağıdaki cebirsel ifadeleri en sade şekilde yazalım.
a) m2-m+m2+m = ? => 2m2
b) 2x2-3x-5x-4x2+8 = ? => -2x2-8x+8
c) x2- (x-1)2+x = ? => x2-x2+2x-1+x = 3x-1
d) (x-1)2+(x+2)2= ? => (x2-2x+1)+(x2+4x+4)
(x-1)2+(x+2)2= x2-2x+1+x2+4x+4
(x-1)2+(x+2)2= 2x2+2x+5
Kastamonu Matematik | www.kastamonumatematik.com
Kastamonu Matematik | www.kastamonumatematik.com
Kastamonu Matematik | www.kastamonumatematik.com
Kastamonu Matematik | www.kastamonumatematik.com
Rasyonel Sayı: a bir tam sayı, b sıfırdan farklı bir tam sayı olmak üzere  şeklinde yazılabilen sayılara rasyonel sayılar denir. Payda sıfır olursa tanımsız bir ifade olur.Q sembolü ile gösterilir.
şeklinde yazılabilen sayılara rasyonel sayılar denir. Payda sıfır olursa tanımsız bir ifade olur.Q sembolü ile gösterilir.

Basit Kesir: Payı küçük paydası büyük olan kesirlerdir.
Bileşik Kesir: Payı büyük paydası küçük olan kesirlerdir.Pay ve paydası aynı olan kesirlerde bileşik kesirdir.
Tamsayılı Kesir: Bir sayma sayısı ve bir basit kesir ile birlikte yazılan kesirlerdir.Her bileşik kesir aynı zamanda tamsayılı kesirdir.
Bileşik kesirler tam sayılı kesre çevrilirken;
Pay paydaya bölünür.Bölüm tam sayı,kalan pay,bölen payda olarak yazılır.
Rasyonel Sayıların Sayı Doğrusunda Gösterilmesi:
Pozitif işaretli basit kesirler sayı doğrusunda her zaman 0 ile 1 arasında gösterilir.
Negatif işaretli basit kesirler sayı doğrusunda her zaman -1 ile 0 arasında gösterilir.

Bileşik kesirler sayı doğrusunda gösterilmeden önce tam sayılı kesre dönüştürülür.Tam sayılı kesre sıfırdan başlayarak tam sayı kadar yol aldırılır.Daha sonra şu yol izlenir.Bir sonraki tam sayıya kadar olan aralık,tamsayının yanındaki kesrin paydası kadar parçalanarak pay kadar yol aldırılır.
Her tam sayı aslında bir rasyonel sayıdır.Çünkü her tam sayının altında gizli 1 vardır.Bunu açığa çıkartınca sayı rasyonel sayıya dönüşür.
N: Doğal sayılar, Z: Tam sayılar, Q: Rasyonel sayılar


Yukarıda görüldüğü gibi ondalık kesirler ve devirli ondalık açılımlar birer rasyonel sayıdır.
Rasyonel Sayılarda Sıralama:
Pozitif rasyonel sayılarda sıralama yaparken paydalar eşitlenir,payı büyük olan büyüktür.
Pozitif rasyonel sayılarda sıralama yaparken paylar eşitlenirse,paydası büyük olan küçüktür.
Negatif rasyonel sayılarda sıralama yaparken, pozitif rasyonel sayılardaki gibi sıralama yapılır.Sonra sıralamanın tam tersi alınır.

Negatif ve pozitif rasyonel sayılar karışık verilirse yine payda eşitlenir.Negatif olanların daima küçük,pozitif olanların daima büyük olduğu unutulmamalıdır.
Rasyonel sayıları sıralarken sayı doğrusuna da kullanabiliriz.Sağdan kalanlar hep büyük olur,solda kalanlar hep küçük olur.

İrrasyonel Sayılar ve Gerçek Sayılar

TAM SAYILARLA İŞLEMLER (video)
Tam sayılarla toplama ve çıkarma işlemleri yaparken sayıları n işaretlerine göre hareket edeceğiz.Aynı işaretli tam sayılar toplanırken çoğalır yani fazlalaşır işaretleri aynı kalır.
(-25)+(-12)=-25-12=-37 buradaki işaret değişmedi.
(+25)+(+12)=+25+12=+37 buradaki işaret değişmedi.
Farklı işaretli tam sayılar toplanırken büyük sayıdan küçük sayı çıkarılır.Mutlak değerce büyük sayının işareti sonucun işareti olur.
(-25)+(+12)=-25+12=-13 burada mutlak değerce büyük sayının işareti geldi.
(+25)+(-12)=+25-12=+13 burada mutlak değerce büyük sayının işareti geldi.
Aynı işaretli tam sayılar çıkarılırken birinci sayıyı aynen yazıyoruz ikinci sayının işaretini değiştiriyoruz.Bu iki sayı birbirinden çıkartılıp işaret ise mutlak değerce büyük sayının işareti olur.
(-25)-(-12)=-25+12=-13 burada mutlak değerce büyük sayının işareti geldi.
(+25)-(+12)=+25-12=+13 burada mutlak değerce büyük sayının işareti geldi.
(+2)-(+4)=+2-4=-2 burada mutlak değerce büyük sayının işareti geldi.
(-18)-(-58)=-18+58=+40 burada mutlak değerce büyük sayının işareti geldi.
Farklı işaretli tam sayılar çıkarılırken birinci sayıyı aynen yazıyoruz ikinci sayının işaretini değiştiriyoruz.Bu iki sayıyı birbiri ile topluyoruz işaret ise aynı işaret oluyor.
(-25)-(+12)= -25-12=-37 buradaki işaret değişmedi.
(+25)-(-12)= +25+12=+37 buradaki işaret değişmedi.
(-30)-(+40)= -30-40=-70 buradaki işaret değişmedi.
(+11)-(-12)= +11+12=+33 buradaki işaret değişmedi.
Tam sayılarla çarpma işlemi yaparken:
Aynı işaretli sayıların çarpılması aynen çarpılır ve işaretleri hep pozitif olur.
(-25)x(-4)=+100
(+25)x(+4)=+100
Farklı işaretli sayıların çarpılması aynen çarpılır ve işaretleri hep negatif olur.
(-25)x(+4)=-100
(+25)x(-4)=-100
Tam sayılarla bölme işlemi yaparken:
Aynı işaretli sayıların bölünmesi aynen bölünür ve işaretleri hep pozitif olur.
(-20):(-4)=+5
(+20):(+4)=+5
Farklı işaretli sayıların bölünmesi aynen bölünür ve işaretleri hep negatif olur.
(-20):(+4)=-5
(+20):(-4)=-5
Tam Sayılarda Pullarla İşlemler
Tam Sayılarda Pullarla Toplama İşlemi:
Tam sayılarda pullarla toplama işlemi yaparken,ilk sayı kadar pul kutuya konur.Eklenecek sayı kadar pul kutuya ilave edilir.Kutunun içindeki pulların hepsi + işaretli ise toplanır ve sonuç + olarak yazılır.Kutunun içindeki pulların hepsi – işaretli ise toplanır ve sonuç - olarak yazılır.Eğer kutunun içindeki pullar – ve + işaretli ise,aynı sayıdaki – ve + pullar birbirini yer.Arta kalan pullar işaretleri ile birlikte sonuç olarak yazılır. (+6)+(-2)=+4

Örnek: Aşağıdaki pullarla verilen işlemin matematik cümlesini yazıp açıklayınız.
Yukarıdaki soruda aslında en başta -5 pul duruyormuş.Sonradan +3 pul eklenmiş.Kutunun içinde - pul ile + pul yanyana gelince birbirini yer yani götürür. -3 pul +3 pulu yedi.Geriye -2 pul kaldı.Doğru cevap D şıkkıdır.
Örnek: Aşağıdaki pullarla verilen işlemin matematik cümlesini yazıp açıklayınız.
Yukarıdaki soruda aslında en başta +2 pul duruyormuş.Sonradan +3 pul eklenmiş.Kutunun içinde +5 oldu. (+2)+(+3)=+5
Tam Sayılarda Pullarla Çıkarma İşlemi:
Tam sayılarda pullarla çıkarma işlemi yaparken,ilk sayı kadar pul kutuya konur.Çıkarılacak sayı kadar kutuya – ve + işaretli pul konur.Çıkması gereken pullar kutudan çıktıktan sonra, kalan pullar kutuda sayılır.Eğer kutunun içinde – ve + işaretli kalmış olursa aynı sayıda olanlar birbirini yer.Arta kalan pullar işaretleri ile birlikte sonuç olarak yazılır.(-4)-(+3)=(-7)

Örnek: Aşağıdaki pullarla verilen işlemin matematik cümlesini yazıp açıklayınız.
Yukarıdaki soruda aslında en başta -7 pul duruyormuş.Kutudan -3 pul çıkarılmış.Geriye -4 pul kaldı. (-7)-(-3)=-4
Örnek: Aşağıdaki pullarla verilen işlemin matematik cümlesini yazıp açıklayınız.
Yukarıdaki soruda aslında en başta +9 pul duruyormuş.Kutudan +10 pul çıkarılmış.Yanlız +10 pul çıkarmak için kutunun içine +1 ve -1 pul ilave edilir.Daha sonra +10 pul çıkarılır.Geriye -1 pul kaldı. (+9)-(+10)=-1
Tam Sayılarda Pullarla Çarpma İşlemi:
5 x (-3) çarpma işlemi yapılırken kutunun içerisine 5 tane 3’lü – pul girer.Sonuçta kutunun içinde 15 tane – pul olacak.

(-3) x 5 çarpma işlemini yaparken kutunun içine 3 tane 5’li sıfır çifti pul girer.Sonra kutunun içinden 3 tane 5’li + pul çıkar.Burada ikinci sayı +5 olduğu için + pullar dışarı çıkar.

(-3) x (-4) çarpma işlemini yaparken kutunun içine 3 tane 4’lü sıfır çifti pul girer.Sonra kutunun içinden 3 tane 4’lü - pul çıkar.Burada ikinci sayı -4 olduğu için - pullar dışarı çıkar.

Tam Sayılarda Pullarla Bölme İşlemi:
8 : 2 bölme işlemi yapılırken kutunun içerisine 8 tane + pul girer.Pullar iki gruba ayrılır.Her gruptaki pul sayısı sonucu verir.(8):(2)=+4

(-14) : 7 bölme işlemi yapılırken kutunun içerisine 14 tane – pul girer.Pullar yedi gruba ayrılır.Her gruptaki pul sayısı sonucu verir.(-14):(7)=-2

Tam Sayılarda İşlemlerin Sayı Doğrusunda Gösterilmesi:
Eklenen sayı pozitifse sağa doğru, eklenen sayı negatifse sola doğru ilerlenir.
(+4)+(-8)=(-4)

Örnek: Aşağıdaki sayı doğrusunda verilen işlemin matematik cümlesini yazıp açıklayınız.
Doğru cevap A şıkkıdır.
Örnek: Aşağıdaki sayı doğrusunda verilen işlemin matematik cümlesini yazıp açıklayınız.
Çıkarma işlemi olduğu için çıkan sayı pozitifse sola ilerlenir,çıkan sayı negatifse sağa ilerlenir.
(+6)-(+3)=+3
Örnek: Aşağıdaki sayı doğrusunda verilen işlemin matematik cümlesini yazıp açıklayınız.
Çıkarma işlemi olduğu için çıkan sayı pozitifse sola ilerlenir,çıkan sayı negatifse sağa ilerlenir.
(-6)-(-10)=+4
TAM SAYILAR KABİLESİ
Günün birinde Kafkas dağlarının ardında bir kabile yaşarmı...ş .Bu kabilenin adı tam sayılar kabilesiymiş.Bu kabile iki kola ayrılırmış.Bunlardan biri NEGATİF tam sayılar olup bu tam sayılar diğer kabilelere hep öfke aşılarmış.Fakat tam sayıların diğer kolu olan POZİTİF tam sayılarla yaptıkları her savaşta yenilirlermiş, çünkü pozitif tam sayılar hep mutluluk aşıladıkları için öfkeye hiç yenilmezlermiş.Bir de ‘0’ sayısı varmış.Bu kendi halinde ,kimseye yararı ve zararı olmayan , etliye sütlüye karışmayan birisiymiş.Ama sinirlendiğinde çok kötü çarparmış.Bu yüzden kimse onunla çatışmayı göze alamazmış.Zamanla tam sayılar arasındaki ayrılık alevlenmiş ve pozitif tam sayılar arasından bir grup ayrılıp ,kendilerine DOĞAL sayılar diyerek başka bir kabile kurmuş. Bu grup ‘0’ da yanlarına almış ve negatif tam sayılardan uzakta bir mekana çadır kurmuşlar.Uzun zaman sonra negatif tam sayılar ne kadar büyük bir hata yaptıklarını anlamışlar ama nafile… Aralarından en yaşlı ve bilge olanlarını seçip bir komite kurmuşlar ve doğal sayılarla anlaşma imzalamak için göndermişler.Uzun uğraşlar sonucunda antlaşma imzalanmış.Buna göre; negatif tam sayılar ve doğal sayılar beraberce yaşayacaklar ama doğal sayılar ( sıfır hariç) eskisi gibi pozitif tam sayı olarak anılacak ve hep beraber aynı yerde yaşayacaklardır.Hemen işe koyulmuşlar ve sayı doğrusu denen yeni evlerini yapmaya başlamışlar.Evlerinin yerini belirlemeye gelince ne yapacaklarını şaşırmışlar , herkes en güzel yeri isterken sıfır araya girmiş ve ‘ benim solumda negatif tam sayılar sağımda da pozitif tam sayılar oturacak ben tam ortada olacağım.’ Herkes bu kararı çok sevmiş ve kabul etmiş. O günden bugüne hiç kavga etmeden yaşaya gelmişler.
Kastamonu Matematik | www.kastamonumatematik.com
 boyutlarından biri bir olan bir küpün kapladığı hacime eşittir.
boyutlarından biri bir olan bir küpün kapladığı hacime eşittir.  biner biner büyürler.
biner biner büyürler. 
 bir metreküp içinde 1 000 000 santimetreküp bulunur.
bir metreküp içinde 1 000 000 santimetreküp bulunur. 
 bir desimetreküpte 1 000 000 milimetreküp
bir desimetreküpte 1 000 000 milimetreküp bir metreküpte 1 000 000 000 milimetreküp bulunur.
bir metreküpte 1 000 000 000 milimetreküp bulunur.
 o birimi gösteren tamsayı yazılır
o birimi gösteren tamsayı yazılır sonra sağına bir virgül konur. Bundan sonra da askatları üçlü rakamlar halinde yazılır. Sayının sağına da o birimin kısaltılmışı yazılır. Okunuşta her basamak
sonra sağına bir virgül konur. Bundan sonra da askatları üçlü rakamlar halinde yazılır. Sayının sağına da o birimin kısaltılmışı yazılır. Okunuşta her basamak kendi birimine göre okunur.
kendi birimine göre okunur. boy ve yüksekliktir.Bir cismin hacmi o cismin içini dolduran birim küplerin sayısına eşittir.Hacim V harfi ile gösterilir.
boy ve yüksekliktir.Bir cismin hacmi o cismin içini dolduran birim küplerin sayısına eşittir.Hacim V harfi ile gösterilir.
 tabana yerleşmiş olan 9 küpten yukarıya doğru 3 sıra daha konulur.Böylece
tabana yerleşmiş olan 9 küpten yukarıya doğru 3 sıra daha konulur.Böylece

 hacmi 1 santimetreküp olan küplerden 4 x 2 = 8 tane yerleştirilmiştir.Prizmanın yüksekliği 3 cm olduğundan şeklin tamamına 3 x 8 = 24 küp yerleşir.Prizmanın hacmine V dersek;
hacmi 1 santimetreküp olan küplerden 4 x 2 = 8 tane yerleştirilmiştir.Prizmanın yüksekliği 3 cm olduğundan şeklin tamamına 3 x 8 = 24 küp yerleşir.Prizmanın hacmine V dersek;

 b
b c olan bir dikdörtgenler prizmasının hacmi
c olan bir dikdörtgenler prizmasının hacmi


Kastamonu Matematik | www.kastamonumatematik.com
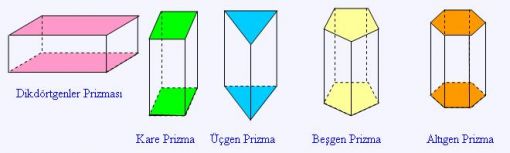
Kastamonu Matematik | www.kastamonumatematik.com
 süt
süt zeytinyağı
zeytinyağı pekmez
pekmez benzin
benzin mazot
mazot gazyağı
gazyağı ilaç
ilaç kolonya vb gibi sıvıları ölçmek için kullanılan ölçülere sıvı ölçüleri denir.Sıvı ölçüsü birimi litredir.Sıvıları ölçmeye yarayan ve hacmi 1 desimetreküp olan kaba da litre denir.
kolonya vb gibi sıvıları ölçmek için kullanılan ölçülere sıvı ölçüleri denir.Sıvı ölçüsü birimi litredir.Sıvıları ölçmeye yarayan ve hacmi 1 desimetreküp olan kaba da litre denir.
 santilitre ve mililitredir.
santilitre ve mililitredir.

 onar onar küçülür.
onar onar küçülür. litrenin katları cinsinden yazınız.
litrenin katları cinsinden yazınız. 2 dekalitre
2 dekalitre 32 hektolitre
32 hektolitre 432 kilolitre olur.
432 kilolitre olur. litrenin askatları cinsinden yazınız.
litrenin askatları cinsinden yazınız. 3 dal
3 dal 75
75 3 dekalitre olur.
3 dekalitre olur.
 40 cm ve 15 cm olan dikdörtgenler prizması şeklindeki bir kap kaç litre sıvı alır?
40 cm ve 15 cm olan dikdörtgenler prizması şeklindeki bir kap kaç litre sıvı alır? desimetreküpe çeviririz.Çünkü litre ile desimetreküp eşittir.
desimetreküpe çeviririz.Çünkü litre ile desimetreküp eşittir.Kastamonu Matematik | www.kastamonumatematik.com
 alan ölçüleri denir. Alan ölçüleri de metre sistemine göre düzenlenmiştir.
alan ölçüleri denir. Alan ölçüleri de metre sistemine göre düzenlenmiştir. bir kenarı bir metre uzunluğunda olan bir karenin alanıdır.
bir kenarı bir metre uzunluğunda olan bir karenin alanıdır. 
 askatları yüzer yüzer küçülür.
askatları yüzer yüzer küçülür.  metrekarenin askatları ile ölçülür. Metrekarenin askatları
metrekarenin askatları ile ölçülür. Metrekarenin askatları bir metrekarenin 100
bir metrekarenin 100 10.000
10.000 1.000.000 eşit parçaya bölünmesiyle elde edilmiştir.
1.000.000 eşit parçaya bölünmesiyle elde edilmiştir.  1 desimetrekare denir.
1 desimetrekare denir.

 1 santimetrekare denir.Bir desimetrekarenin yüz defa küçüğüdür.
1 santimetrekare denir.Bir desimetrekarenin yüz defa küçüğüdür. 

 100 santimetrekare vardır.
100 santimetrekare vardır. 1 milimetrekare denir.Bir santimetrekarenin yüz defa küçüğüdür.
1 milimetrekare denir.Bir santimetrekarenin yüz defa küçüğüdür. 
 bir metrekarede 1.000.000 milimetrekare vardır.
bir metrekarede 1.000.000 milimetrekare vardır. 1 dekametrekare denir.1 metrakarenin 100 kat büyüğüdür.
1 dekametrekare denir.1 metrakarenin 100 kat büyüğüdür.
 10.000 metrekare vardır.
10.000 metrekare vardır.
 10.000 dekametrekare
10.000 dekametrekare 1.000.000 metrekare vardır.
1.000.000 metrekare vardır. 

 hangi birime göre yazılacaksa
hangi birime göre yazılacaksa o birimi gösteren tam sayı yazılır
o birimi gösteren tam sayı yazılır sonra sağına bir virgül konur. Bundan sonra da askatları
sonra sağına bir virgül konur. Bundan sonra da askatları çift rakamlar halinde yazılır Sayının sağına da o birimin kısaltılması konur. Okunuşta
çift rakamlar halinde yazılır Sayının sağına da o birimin kısaltılması konur. Okunuşta her basamak
her basamak kendi birimlerine göre okunur.
kendi birimlerine göre okunur. 
 herhangi bir alan ölçüsü birimine çevrilerek yazılabilir. Alan ölçülerinden verilen sayıyı başka bir birime çevirmek için
herhangi bir alan ölçüsü birimine çevrilerek yazılabilir. Alan ölçülerinden verilen sayıyı başka bir birime çevirmek için bu birimin
bu birimin ilk birimin katı ya da askatı olup olmadığına bakılır. Çevrilmek istenin birim
ilk birimin katı ya da askatı olup olmadığına bakılır. Çevrilmek istenin birim çevrilecek birimin askatı ise
çevrilecek birimin askatı ise virgül o kadar basamak sağa alınır. Katı ise virgül o kadar basamak sola alınır. Virgül iki basamak sağa alınınca
virgül o kadar basamak sağa alınır. Katı ise virgül o kadar basamak sola alınır. Virgül iki basamak sağa alınınca önceki birim
önceki birim kendinden bir küçük olan birime çevrilmiş olur. Virgül iki basamak sola alınınca önceki birim
kendinden bir küçük olan birime çevrilmiş olur. Virgül iki basamak sola alınınca önceki birim kendinden bir büyük büyük birime çevrilmiş olur.
kendinden bir büyük büyük birime çevrilmiş olur.
 bahçe
bahçe tarla gibi yerler arazi ölçüleri ile ölçülür.Arazi ölçüleri ar
tarla gibi yerler arazi ölçüleri ile ölçülür.Arazi ölçüleri ar dekar ve hektardır.
dekar ve hektardır. 1 dekametrekarelik bir alana eşittir.
1 dekametrekarelik bir alana eşittir.


 onar onar küçülür.
onar onar küçülür.









 dikdörtgenin alanından çıkarırız.
dikdörtgenin alanından çıkarırız.




 alttaki prizmaya çakıştığı için hesaplanması gereken 5 yüzü vardır.Bu nedenle
alttaki prizmaya çakıştığı için hesaplanması gereken 5 yüzü vardır.Bu nedenle
Kastamonu Matematik | www.kastamonumatematik.com
UZUNLUK ÖLÇME (video)
Uluslararası Ölçüm Sisteminin uzunluk birimi metre'dir ve kısaca "m" ile gösterilir. Günümüzde "1 metre", ışığın boşlukta 1/299,792,458 saniyede aldığı yol olarak tanımlanmıştır.Bu çağdaş tanım günümüzde dünyanın çeşitli laboratuarlarında yapılabilen hassas ölçümlerin birbirleriyle karşılaştırılabilmesi amacıyla kabul edilmiştir.
Günlük hayatta bazen metreden çok daha küçük ya da daha büyük uzunlukları ölçme ihtiyacı olur.Bu durumlarda metredene daha küçük ve daha büyük birimler kullanmak zorunda kalırız.Metreden küçük uzunlukları ölçmede metrenin askatlarını metreden büyük uzunlukları ölçmede de metrenin katlarını kullanırız.
metreden büyük uzunlukları ölçmede de metrenin katlarını kullanırız.
METRENİN ASKATLARI
Metrenin askatları; desimetre santimetre ve milimetredir.
santimetre ve milimetredir.
1. Desimetre:
Metrenin onda biri uzunluğundaki ölçme birimidir.Kısaca dm harfleri iel gösterilir.
2. Santimetre:
Metrenin yüzde biri uzunluğundaki uzunluk ölçüsü birimidir. Kısaca cm harfleri ile gösterilir.
3. Milimetre:
Metrenin binde biri uzunluğundaki uzunluk ölçüsü birimidir.Kısaca mm harfleri ile gösterilir.
METRENİN KATLARI
Metrenin katları; dekametre hektometre ve kilometredir.
hektometre ve kilometredir.
1. Dekametre:
Metrenin 10 katı uzunluğundaki uzunluk ölçüsü birimidir.Kısaca dam olarak gösterilir.
1 dam = 10 m
2. Hektometre:
Metrenin 100 katı uzunluğundaki uzunluk ölçme birimidir.Kısaca hm ile gösterilir.
1 hm = 100 m
1 hm = 10 dam
3. Kilometre:
Metrenin 1000 katı uzunluğundaki uzunluk ölçme birimidir.Kısaca km ile gösterilir.
1 km = 1000 m
1 km = 10 hm
1 km = 100 dam
Uzunluk ölçüleri onar onar büyür onar onar küçülür.
onar onar küçülür. 
Herhangi bir uzunluk ölçüsü birimini alt birimlere çevirmek için 10 veya 10'un kuvvetleri ile çarparız.
7 m = ... dm
7x10= 70 dm
12 dm = ... cm
12x10 =120 cm
28 67 cm = ... mm
67 cm = ... mm
28 67x10 = 286
67x10 = 286 7 mm gibi
7 mm gibi
Herhangi bir uzunluk ölçüsü birimini üst birimlere çevirmek için 10 veya 10'un kuvvetlerine böleriz.
2500 m = .... dam
2500 : 10 = 250 dam
1680 dam = .... km
1680 : 100 = 16 80 km
80 km
550 m = .... hm
550 : 100 = 5 5 hm gibi
5 hm gibi
ÖRNEK:
8 km 6 hm 4 dam 2 m = ............... m
8 km = 8x 1000 = 8000 m
6 hm = 6 x 100 = 600 m
4 dam = 4 x 10 = 40 m
2 m = 2 x 1 = 2 m
8000 + 600 + 40 + 2 = 8642 m olur.
Verilen bir ölçüdeki rakamların hangi ölçü birimini gösterdiğini bulmak için; verilen birimin cinsine bakarız.O birim eğer sayı tam sayı ise en sondaki basamağı gösterir.Sonraki basamakları ölçü merdivenindeki sıraya göre yerleştiririz.
eğer sayı tam sayı ise en sondaki basamağı gösterir.Sonraki basamakları ölçü merdivenindeki sıraya göre yerleştiririz.
Eğer sayı ondalık sayı ise; tam sayı kısmındaki sağdaki en son basamak verilen birimi gösterir.Diğer basamakları merdivendeki sıraya göre yerleştiririz.
3621 metrede hm yi gösteren basamağı bulalım.
Kastamonu Matematik | www.kastamonumatematik.com
ÜÇGENLER (video)
Üçgenler kenar uzunluklarına göre üçe ayrılır
Çeşit kenar üçgen; her kenarı farklı uzunlukta olan üçgenlerdir
İkiz kenar üçgen; iki kenar uzunluğu eşit olan üçgenlerdir
Eşkenar üçgen; bütün kenarları aynı uzunlukta olan üçgenlerdir
Üçgenler açılarına göre 3'e ayrılır
Dar açılı üçgen; bütün açıları 90° den küçük olan üçgenlerdir.
Dik açılı üçgen; bir açısı 90° olan üçgenlerdir
Geniş açılı üçgen; bir açısı 90° ile 180° arasında olan üçgenlerdir
a) Bütün kenarları birbirine eşittir.
b) Komşu kenarları birbirine diktir.
c) Köşegen uzunlukları birbirine eşittir.
ç) Köşegenler birbirini dik keserek ortalar.
d)Köşelerde oluşan komşu tümler açılar eştir.
e) Köşegenlerden biri tarafından iki eş parçaya ayrılır.
a) Karşılıklı kenarları aynı uzunlukta ve birbirine paraleldir.
b) Komşu kenarları birbirine diktir.
c) Köşegen uzunlukları birbirine eşittir.
ç) Köşegenler birbirini ortalar.
d) Köşegenlerden biri tarafından iki eş parçaya ayrılır.
Bir nesnenin bir yerden başka bir yere belirli bir doğrultu ve yönde kayma hareketi öteleme olarak adlandırılır.
Ötelemede bir şeklin duruşu, biçimi ve boyutları aynı kalır. Bir şeklin kendisi ile öteleme altındaki görüntüsü eş ve simetriktir. Fakat bu simetri, doğruya göre alınan simetriden farklıdır. Özel olan bu tür simetriler “öteleme simetrisi” olarak adlandırılır.
Kastamonu Matematik | www.kastamonumatematik.com
Kastamonu Matematik | www.kastamonumatematik.com
ASAL SAYILAR (video)
Asal sayılar yalnız ve yalnız iki pozitif tamsayı böleni olan doğal sayılardır. Asal sayılar, sadece kendisi ve 1 sayısına bölünebilen 1'den büyük pozitif tam sayılar biçiminde de tanımlanabilir.En küçük asal sayı 2 dir.2 sayısı asal sayıların içinde çift olan tek sayıdır.


Kastamonu Matematik | www.kastamonumatematik.com
ÜSLÜ SAYILAR (video)
a,b,n birer doğal sayı olmak üzere;
an = b üslü niceliğinde a’ya taban,
kaç tane a’nın çarpıldığını belirten sayı olan n’ye kuvvet veya üs, b’ye de değer adı verilir.
an ifadesi (a üssü n) veya (a’nın n. kuvveti) olarak okunur.
Bir sayının kendisi ile tekrarlı çarpımı, o sayının kuvveti olarak adlandırılır.Bu tekrarlı çarpımın sonucunu bulmaya kuvvet alma işlemi denir.Kuvvet kelimesi ile üs kelimesi eşdeğerdir.
a.a.a.a.a…..a=an (n tane a’nın çarpımı)
3x3x3x3x3=35 (5 tane 3’ün yan yana yazılıp çarpılmasıdır.)
2x2x2x2x2x2x2x2x2=29
Sıfırdan farklı her sayının sıfırıncı kuvveti 1’e eşittir.Sıfırın sıfırıncı kuvveti tanımsızdır.
70=1
00=tanımsız
101=10
102=100
103=1000
104=10000
(17)2 = 17.17=289
34= 3.3.3.3=81
Kastamonu Matematik | www.kastamonumatematik.com


Kastamonu Matematik | www.kastamonumatematik.com


Kastamonu Matematik | www.kastamonumatematik.com








a ve b reel sayılarının en az biri sıfırdan farklı olmak üzere,a/b ye a nın b ye oranı denir.
ORANTI NEDİR?
En az iki oranın eşitliğine orantı denir. Yani a/b oranı c/d nin eşitliği olan a/b=c/d ye orantı denir.
ise, a/b=c/d a ile d ye dışlar, b ile c ye içler denir.
ORANTININ ÖZELLİKLERİ NELERDİR?
1) a/b=c/d ise a.d= b.c
2) a : b : c = x : y : z ise,
Burada, a = x . k
b = y . k
c = z . k dır.
ORANTI ÇEŞİTLERİ NELERDİR?
1. Doğru Orantılı Çokluklar
Orantılı iki çokluktan biri artarken diğeri de aynı oranda artıyorsa ya da biri azalırken diğeri de aynı oranda azalıyorsa bu iki çokluk doğru orantılıdır denir.
x ile y doğru orantılı ve k pozitif bir doğru orantı sabiti olmak üzere, y = k . x ifadesine doğru orantının denklemi denir. Bu denklemin grafiği aşağıdaki gibidir.
İşçi sayısı ile üretilen ürün miktarı doğru orantılıdır.
2. Ters Orantılı Çokluklar
Orantılı iki çokluktan biri artarken diğeri aynı oranda azalıyorsa ya da biri artarken diğeri aynı oranda azalıyorsa bu iki çokluk ters orantılıdır denir.
x ile y ters orantılı ve k pozitif bir ters orantı sabiti olmak üzere,y=k/x ifadesine ters orantının denklemi denir.
Bu denklemin grafiği aşağıdaki gibidir.
a, b ile doğru c ile ters orantılı ve k pozitif bir orantı sabiti olmak üzere,
a.c/b=k
ARİTMETİK ORTALAMA
n tane sayının aritmetik ortalaması bu n sayının toplamının n ye bölümüdür.
Buna göre, x1, x2, x3, ... , xn sayılarının aritmetik ortalaması,
X1+x2+x3+…..xn / n dir.
Bu n tane sayının herbiri; A ile çarpılır, B ilave edilirse oluşan yeni sayıların aritmetik ortalaması Ax + B olur.
GEOMETRİK ORTALAMA
n tane sayının geometrik ortalaması bu sayıların çarpımının n. dereceden köküdür.
Buna göre,
a ile b nin aritmetik ortalaması geometrik ortalamasına eşit ise a = b dir.
DÖRDÜNCÜ ORANTILI
a/b=c/x orantısını sağlayan x sayısına a, b, c sayıları ile dördüncü orantılı olan sayı
Kastamonu Matematik | www.kastamonumatematik.com
ONDALIK KESİRLER (video)
Paydası 10 veya 10’un kuvveti olacak şekilde genişletilebilen kesirlere ondalık kesir denir.Yada virgüllü olarak gördüğümüz ifadelere ondalık sayı denir.Bazı kitaplarda ondalık kesir veya ondalık sayı kullanılır.
Örneğin 3,74 ondalık kesrindeki 3’e tam kısım, 74’e kesir kısım denir.
Devirli Ondalıklı Kesir: Paydası 10 veya 10’un kuvveti olacak şekilde genişletilemeyen kesirlerin, ondalık açılımlarının kesir kısımlarında tekrar eden rakamlar bulunur.Bu tür ondalık kesirler devirli ondalık kesir olarak adlandırılır.Yani virgülün sağında tekrar eden belli sayılar varsa bu tür ifadeler devirli ondalık sayılar denir.Bu tekrar eden sayı veya sayıların üzerine devir çizgisi çekerek durdurmuş oluruz.
Devirli ondalık kesre karşılık gelen kesri yani rasyonel sayıyı bulmak için izlenecek yol;
Pay için, sayı aynen yazılır devretmeyen kısım çıkarılır. Payda için, virgülden sonra devreden sayı kadar 9, devretmeyen sayı kadar 0 yazılır.
Ondalık Kesirlerde Sıralama
Ondalık kesirlerde sıralama yaparken önce tam kısımlara bakılır.Tamı büyük olan büyüktür.Eğer tam kısımlar eşitse hemen bir sağdaki onda birler basamağına bakılır.Onda birler basamağı büyük olan büyüktür.Buda eşitse hemen bir sağdaki yüzde birler basamağına bakılır.Yüzde birler basamağı büyük olan büyüktür.Buda eşitse hemen bir sağdakine bakılır.Sıralamada izlenecek yol bu şekilde devam eder
Ondalık Kesirlerde Çözümleme ve Yuvarlama
Çözümleme yaparken virgülün sağı kesir kısım,virgülün solu tam kısım olduğu unutulmamalıdır.
Örnek: 245,326 ondalık kesrini çözümleyelim.
(2x100)+(4x10)+(5x1)+(3x0,1)+(2x0,01)+(6x0,001)
200+40+5+0,3+0,02+0,006 = 245,326
Ondalık kesirleri istenilen basamağa göre yuvarlarken, verilen basamağın sağındaki ilk rakam ile 5 arasında karşılaştırma yapılır.
Örnek: 0,54 ondalık kesrini onda birler basamağına göre yuvarlayalım.
Verilen basamakta 5 var. 5’in sağına bakarız. 4<5 olduğundan ekleme yapılmaz.Diğerleri atılır.Yuvarlanmış hali ise 0,5 olur.
Örnek: 0,287 ondalık kesrini yüzde birler basamağına göre yuvarlayalım.
Verilen basamakta 8 var. 8’in sağına bakarız. 7>5 olduğundan 1 ekleme yaparız.Diğerleri atılır.Yuvarlanmış hali ise 0,29 olur.
Örnek: 16,51 ondalık kesrini tam sayı olarak yuvarlayalım.
Verilen basamakta 6 var. 6’nın sağına bakarız. 5=5 olduğundan 1 ekleme yaparız.Diğerleri atılır.Yuvarlanmış hali ise 17 tam olur.
Ondalık Kesirlerde Toplama ve Çıkarma İşlemleri
Ondalık kesirler toplanırken veya çıkarılırken, virgüller alt alta gelecek şekilde yazılır ve doğal sayılarda toplama - çıkarma işleminde olduğu gibi toplama - çıkarma işlemi yapılır. Sonuç, virgüllerin hizasından virgülle ayrılır.
Ondalık Kesirlerde Çarpma
Ondalık kesirlerin çarpımı yapılırken, virgül yokmuş gibi çarpma işlemi yapılır. Çarpılan sayıların virgülden sonraki basamak sayılarının toplamı kadar, sonuçtaki sayıda o kadar sağdan sola doğru virgülle ayrılır.
Ondalık Kesirlerde Bölme
Ondalık kesirlerin bölme işlemi yapılırken, bölen virgülden kurtulacak biçimde 10 un kuvveti ile çarpılır. Bölünen de aynı 10 un kuvveti ile çarpılarak normal bölme işlemi yapılır.Burada her iki sayıda virgülden kurtarılır.
Ondalık kesirlerde 10, 100, 1000 ile kısa yoldan çarpma işlemleri yapmak için sıfır sayısı kadar virgül sağa kayar.Virgülün bittiği yerde sıfır ilave edilir.
Ondalık kesirlerde 10, 100, 1000 ile kısa yoldan bölme işlemleri yapmak için sıfır sayısı kadar virgül sola kayar. Virgülün bittiği yerde sıfır ilave edilir.
Kastamonu Matematik | www.kastamonumatematik.com
Problem: Okan, alfabemizdeki bütün harfleri aynı özelliklere sahip kâğıt parçalarına yazarak boş bir kutuya atmıştır. Emel, kutudan rasgele bir kâğıt çekmiştir.
Çekilen kâğıtta ünlü harf olma olasılığı nedir?
Deney: Eş özelliklere sahip kâğıt üzerine yazılmış olan alfabemizdeki harflerden birinin seçilmesi.
Örnek uzay:
O={alfabemizdeki tüm harfler} veya
Ö={a,b,c,ç,d,e,f,g,ğ,h,ı,i,j,k,l,m,n,o,ö,p,r,s,ş,t,u,ü,v,y,z}, s(Ö)=29
Olay:
H={bir ünlünün çekilmesi}veya H={a,e,ı,i,o,ö,u,ü},
s(H)=8
Olayın çıktıları:
a, e, ı, i, o, ö, u, ü
Eş olasılıklı olma: Her bir harfin çekilme olasılığı eşittir.
Evrensel kümede her bir eleman bir kez yazılır fakat örnek uzayda çıktılar kaç tane ise o kadar yazılır.
Örnek:
a. “MATEMATİK” kelimesinin harflerinden oluşan evrensel küme: E={M, A, T, E, İ, K}
b. “Matematik” kelimesinin her bir harfi aynı özelliklere sahip kâğıt parçalarına yazılarak torbaya atılmıştır.
“Bakmadan bir kâğıt çekildiğinde çıkan harfin “A” olma olasılığı nedir?” sorusundaki örnek uzay:
Ö={M, A, T, E, M, A, T, İ, K}
OLASILIK ÇEŞİTLERİ NELERDİR?
Deneysel olasılık: Bir olasılık deneyi sonunda hesaplanan olasılığa denir. Bu olasılıkta deneyin yapıldığı problemin içinde geçer, problemi okuduğunuzda bir şeyler yapıldığını anlar, verileri görürsünüz.
örnek: Hileli bir zar 20 kez atıldığında 3 kez 1, 2 kez 2, 3 kez 3, 2 kez 4, 3 kez 5 ve 7 kez 6 geliyor. Buna göre bu zar atıldığında 5 gelme olasılığı kaçtır? cevap: 3/20
Teorik olasılık: Bir olasılık deneyinden teorik olarak beklenen olasılığa denir.Genelde şimdiye kadar karşılaştığımız problem tipleridir.İstenen durumların sayısını tespit edip tüm durumlara böleriz.
örnek: Bir zar atıldığında 3 gelme olasılığı kaçtır? cevap: 1/6
Öznel olasılık: Kişilerin kendi düşüncelerine göre karar verdikleri olasılıklara denir.Bu tip problemlerde kişilerin ismi ve tahmini yer alır.
örnek: 25 yumurtadan bazıları çift sarılıdır.Ali'ye göre alınacak bir yumurtanın çift sarılı olma olasılığı 10/25=0,4'tür. Ayşe'ye göre alınacak bir yumurtanın çift sarılı olma olasılığı 15/25=0,6'dır.
Kastamonu Matematik | www.kastamonumatematik.com
AÇI : Aynı doğru üzerinde olmayan, başlangıç noktaları ortak olan iki ışının birleşim kümesine Açı denir.
Açıyı oluşturan iki ışının kesişim kümesine AÇININ KÖŞESİ, bu ışınlara ise AÇININ KOLLARI denir.

1) Işınların nokta adları alınarak:
ABC açısı veya CBA açısı
2) Sadece başlangıç noktası alınarak:
B açısı şeklinde okunur.
Bir açı, bulunduğu bölgeyi üç bölgeye ayırır; (Yukarıdaki şekildeki gibi)
1) Açının Kendisi
2) Açının Dış Bölgesi
3) Açının İç Bölgesi
Açı ölçüsü DERECEDİR. Açıların ölçüsünü bulmak için AÇI ÖLÇER veya İLETKİ kullanılır.
ÖZEL AÇILAR
1) Dar Açı: Ölçüsü 0º `den büyük ve 90º`den küçük açılara Dar açı denir.
2) Dik Açı: Ölçüsü 90º olan açıya Dik Açı denir.
3) Geniş Açı: Ölçüsü 90º`den büyük 180º`den küçük olan açıya Geniş Açı demir.
4) Doğru Açı: Ölçüsü 180º olan açıya Doğru Açı denir.
5) Tam Açı: Ölçüsü 360º olan açıya Tam Açı denir.
6) Tümler Açı: İki açının ölçüleri toplamı 90º olan açıya Tümler Açı denir.
7) Bütünler Açı: İki açının ölçüleri toplamı 180º ise bu açılara Bütünler Açı denir.
Bir Noktada Kesişen İki Doğrunun Oluşturduğu Açılar:
a) Komşu Açılar: Başlangıç noktaları aynı iki veya daha fazla açıya Komşu Açılar denir.
b) Komşu Tümler Açılar: Başlangıç noktaları aynı, ölçüleri toplamı 90º olan iki farklı açıya Komşu Tümler Açılar denir.
c) Komşu Bütünler Açılar: Başlangıç noktaları aynı, ölçüleri toplamı 180º olan açıya Komşu Bütünler Açılar denir.
d) Ters Açılar: Köşeleri ortak ve kenarları birbirine zıt ışınları olan iki açıya Ters Açı denir. Ters açıların ölçüleri birbirine eşittir.
Paralel İki Doğrunun Bir Kesenle Yaptığı Açılar
a) YÖNDEŞ AÇILAR: Şekildeki A ve F, D ve G,
E ve C, B ve H gibi konumlanan açılara
Yöndeş Açılar denir. Yöndeş açılar
birbirine eşittir.
b) TERS AÇILAR: Köşeleri ortak ve kenarları
birbirine zıt ışınları olan iki açıya Ters Açı denir.
Ters açıların ölçüleri birbirine eşittir.
c) DIŞ TERS AÇILAR: Şekildeki G ve A, H ve C açıları gibi konumlanan açılara Dış Ters Açılar denir. Dış ters açıların ölçüleri birbirine eşittir.
d) İÇ TERS AÇILAR:Şekildeki B ve E, D ve F açıları gibi konumlanan açılara İç Ters Açılar denir.
e) KARŞI KONUMLU AÇILAR: Şekildeki B ve F, E ve D açıları gibi konumlanan açılara Karşı Konumlu Açılar denir. Karşı konumlu açıların toplamı 180º`dir.
DOĞRULARIN BİRBİRLERİNE GÖRE DURUMLARI
Paralel doğrular
Elimizde iki doğru olsun bu doğruları, birbirini kesmeyecek şekilde tutarsak paralel doğru olarak adlandırıyoruz. Örneğin; kalorifer petekleri birbirini hiç kesmez. Diğer bir örnek sınıf tahtamızın uzun kenarları birbirini hiçbir zaman kesmez.
Kesişen Doğrular
Eğer doğrular yukarıdaki gibi paralel değilse kesinlikle kesişiyor demektir. Bazen doğrular kesişmiyor gibi durabilir fakat doğruların uçlarını uzattığımızda kesişiyorlarsa bu doğrulara kesişen doğrular denir. Örneğin; “M” harfini düşünürsek M harfindeki her doğru (doğru olarak kabul edersek) birbirini keser.
Dik doğrular
Dik doğrular da aslında kesişen doğrulara dahildir. Sonuçta doğrular ya paraleldir, ya da kesişir. Eğer iki doğru birbiri ile 90 derece açı yapacak şekilde kesişiyorsa, bu tür doğrulara dik kesişen doğrular denir. Örneğin; tahtamızın bir uzun ve bir kısa kenarı dik olarak kesişir.
Kastamonu Matematik | www.kastamonumatematik.com
ÇOKGENLER (video)
Çokgen: Çok kenarlı demektir.
GEN: Kenar anlamına gelir.
Yani; çok kenarlı olan şekillere çokgenler denir. Çokgenin kapalı bir şekil olması gerekmekte.
Bu çokgen en az üç kenardan oluşur;
üçGEN
dörtGEN
beşGEN
altıGEN
diyerek devam eder gider…
Not: Çokgenlerde kenar sayısı,köşe sayısı ve açı sayısı birbirine eşittir.
Örneğin; bir üçgenin 3 kenarı, 3 köşesi ve 3 açısı vardır.
Binlerce üçgen çizebiliriz, binlerce dörtgen de, beşgen de çizebiliriz.
Şimdi bazı özel çokgenlere geçelim;
Adından da anlaşılacağı gibi düzgün, mükemmel olan çokgenlere düzgün çokgenler denir.
Düzgün çokgen; kaçgen olursa olsun ortak özellikleri şunlardır: kenarları ve açıları birbirine eşit olacak !
Başka şart istemiyoruz. Bu şart bizim için yeterli.
En güzel örnek Karedir.
Karenin her kenarı birbirine eşittir ve her açısı da birbirine eşittir. İkisi de bize gerekli… Bu yüzden kare bir düzgün çokgendir.
Fakat dikdörtgen düzgün çokgen değildir !
Tabi neden ama onun da 90 derecelik açıları var dieceksiniz fakat bu yetmez. Kenarlarının da eşit olması gerekir. Dikdörtgenlerins adece karşılıklı kenarları birbirine eşittir. 4 kenarı da birbirine eşit olmadığı için düzgün çokgen değildir.
Diğer düzgün çokgenler:
üç kenarlılar için: eşkenar üçgen
dört kenarlılar için: kare
beş kenarlılar için düzgün beşgen
altı kenarlılar için düzgün altıgen…
diğerleri için de bu şekilde devam eder.
Sadece üç kenarlı ve dört kenarlının özel ismi vardır.
diğerlerinde ise kenar sayısının ününe “düzgün” kelimesini getirmek yeterlidir.
Aşağıdan örnek çokgenlere bakabilirsiniz.
Dikkatli okumanız gereken bir nokta: Tekrar etmekte fayda var. Birçok altıgen çizebilirsiniz, fakat hepsinin uzunlukları birbirine eşit olmaz. Onlar da altıgendir fakat düzgün altıgen denmez, sadece altıgen denir.
Eğer kenarları ve açıları birbirine eşitse buna düzgün altıgen diyebiliriz.
Bu diğer çokgenler için de geçerlidir.
Eşlik ve Benzerlik
Bu konumuz geometri ile ilgili.
Eşlik ve Benzerlik.
Eşlik: Eşlik eşit olan anlamına gelir. İki geometrik cisim düşünün.
Bu cisimler tamamen birbirinin aynısı ise bunlara eş şekiller denir.
İki kare düşünelim ikisinin de her kenarının uzunlukları aynı ise ve görünümleri birbirinin kopyası gibiyse bu şekillere eş şekiller denir.
İki kare daha düşünelim. Birinin kenarları 4 cm, diğerinin kenarları 8 cm ise bunlar eş değildir. Fakat benzerdir.
Benzerlik: En son kısımda benzerlikten bahsettik. Hemen kafanızda şöyle bir soru işareti oluştu. Acaba eş olmayan şekillere benzer şekiller mi diyoruz ?
Öğrencilerimiz Eşliği çok iyi anlar fakat Benzerlik konusunda kafaları karışır.
Benzerlik: iki şekil düşünün, bu şekiller birbirine çok benzemeli fakat birbirinin belli bir oranda büyütülmüş hali olmalı. Hani resimleri büyütürüz ya ? Resim büyütülünce sadece boyumuz mu uzar ? Bedenimizin genişliği de artmaz mı?
İşte benzerlik budur. Şeklin her yöne doğru belli bir oranda artmasıdır.
Elinize kağıt alın ve iki tane dikdörtgen çizin.
Birinin kısa kenarı 3, uzun kenarı 4 olsun.
Diğerinin kısa kenarı 9 uzun kenarı 12 olsun.
Bu dikdörtgen benzerdir.
Çünkü kısa kenarı da 3 karına çıkmış, ( 3.3 =9 )
Uzun kenarı da 3 katına çıkmış. ( 3.4 =12 )
Her ikisi de aynı kat büyüdüğü için şekiller benzerdir.
Şimdi bir dikdörtgen daha çizelim.
Birinin kısa kenarı 3, uzun kenarı 4 olsun.
Diğerinin kısa kenarı 9 uzun kenarı 16 olsun.
Bu dikdörtgenler benzer değildir.
Çünkü kısa kenarı da 3 karına çıkmış, ( 3.3 =9 )
Uzun kenarı da 3 katına çıkmış. ( 4.4 =16)
NOT: İki eş şekil aynı zamanda Benzerdir. fakat her benzer şekil eş değildir.
Çokgenler İBRAHİM HOCA KONU ANLATIMI ve SORULARI VİDEOSU
Kastamonu Matematik | www.kastamonumatematik.com
6.Sınıf Eşlik ve benzerlik çalışma kağıdı indir test eş üçgenler benzer şekiller düzgün çokgenler
1.test:
2.test:
Eşlik ve benzerlik düzgün çokgenler konu testleri eşlik benzerlik sbs hazırlık test soruları 6. sınıf matematik dersi eşlik benzerlik sbs soruları eşlik benzerlik çözümleri indir
ÖRÜNTÜLER, ÖTELEME VE SÜSLEMELER (video)
Örüntü Nedir?
Belirli bir kurala göre düzenli bir şekilde tekrar eden veya genişleyen şekil ya da sayı dizisine örüntü denir. Örüntüler eş yada benzer çokgenler kullanılarak oluşturulur. Örneğin, kağıttan birbirine eş bir sürü üçgen şeklini kestiniz.
Bunlarla bulmaca gibi balık, kuş,ev,halı,kare,dikdörtgen gibi farklı desenlerde yeni şekiller meydana getirebilirsiniz.İşte bu oluşturduğunuz yeni şekillere örüntü adı verilir.
6. Sınıf Örüntü ve Süslemeler konu anlatım videosu
ibrahim tas hocamıza teşekkürler.
Kastamonu Matematik | www.kastamonumatematik.com
Tam sayılarda toplama ve çıkarma işlemi (video)
Geçen dersimizde tam sayılarla ilgili bazı tanımları gördük.
Tam sayılar hem (+) hem de (-) olabiliyordu. Tabi 0 (sıfır) sayısını da unutmamak lazım.
Peki tam sayılarda işlemler nasıl oluyor ?
Eskiden doğal sayılarda işlemleri şu şekilde yapıyorduk;
2+3=5
9-2=7
Peki bu işlem tam sayılarda nasıl olacak ?
Örneğin; Ya iki işaret de (-) olursa ne olacak ?
-3-5 = ? acaba bu bir çıkarma işlemi mi ?
Bunun için şöyle basit bir yöntem kullanabiliriz.
(+) işaretleri alacağımız para olarak, (-) işareti de borcumuz olarak göreceğiz.
Şimdi örnek inceleyelim.
Örnek1) -3-5 = ?
- işaret borç demek oluyordu.
Bir 3 YTL bir de 5 YTL borç almışız.
O halde cebimizdeki paranın son durumu ne olur ?
Cevap: Toplam 8 YTL borcumuz olur. Borç olduğu için 8 in önüne – koyarız.
yani -3-5=-8
Örnek2) -3+8=?
Burada 3 YTL borcumuz var 8 YTL alacağımız var.Cebimizdeki son durum ne olur ?
Borcumuzu ödersek 5 YTL alacaklı oluruz.Alacaklı olduğumuz için cevap + işaretli olur.Yani Sonuç +5 tir.
-3+8=+5
Şimdi aynı mantıkla başka örneklere bakalım:
Örnekler:
+4+7=+11 ( 11 YTL alacak )
+7-11=-4 ( 4 YTL borç )
Peki öğretmenim bazen sayıların önünde 2 tane işaret oluyor. Bu nasıl olacak ? derseniz.
+3-(-4) = ? örneğin bu ? nasıl olur burada sonuç ?
İşte bu tür sorularda önce iki tane yan yana duran işaretleri bir güzel eritip yeni bir işaret çıkarmalıyız yerlerine.
Bunun için şunlara dikkat edelim.
+(+) =+
-(-) =+
+(-) = -
-(+) = -
2 tane (+) yerine bir (+)
2 tane (-) yerine yine 1 (+)
1 (+) ve 1 (-) yerine (-)
1 (-) ve 1 (+) yerine (-)
Kısacası iki işaret yan yana ise; aynı işaretlilerin yerine (+), farklı işaretlileriny erine (-) işareti yazılır.
Şimdi yukarıdaki örneklere bir daha bakalım.
+3-(-4) = ?
önce 2 tane (-) işaretini kaynatıp yerine bir tane oluşturalım.
-(-) yerine + gelir.
Yani +3-(-4) = +3+4 yazabiliriz
Şimdi de bunun sonucunu bulalım
+3+4=+7 oalrak bulunur.
Peki başka bir öenek;
Bu sefer iki sayının önünde de 2 işaret çıksın.
Örneğin;
-(-9)+(-4) = ?
-(-9) yerine +9 yazılır, +(-4) yerine -4 yazılır… ( Bu değişimleri yukarıda verdiğimiz kurala göre yaptık).
Devam edelim;
-(-9) + (-4)
+9-4= +5 oalrak sonuç bulunur.
Kastamonu Matematik | www.kastamonumatematik.com
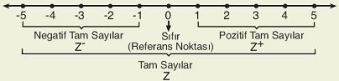
Sıfırın sağındaki sayılar pozitif tam sayılar, sıfırın solundaki sayılar negatif tam sayılardır.Pozitif tam sayılar,negatif tam sayılar ve sıfır sayısının birleşmesi sonucu tam sayılar kümesi oluşur.
Artı işareti olan pozitif sayılar (1,3,45,78,...), eksi işareti olan negatif sayılar(-2,-9,-34,-345,...) ve sıfırında dahil olduğu Z sembolü ile gösterilen sayılardır(....-3,-2,-1,0,+1,+2,+3,...)
Tam sayılar denince sayının önünde artı yada eksi işareti varmı diye bakacaz. Artı işareti yoksada artıdır.
Bugün Manisa'da hava sıcaklığı sıfırın altında 2 derece (-2)
Denizaltı deniz seviyesinin 75 metre altındadır (-75)
THY uçağı şuan yerden 200 metre yüksektedir (+200)
Ali'nin karı 15 ytl (+15)
Ayşe'nin zararı 20 ytl (-20)
sayıyla artı tam sayı toplanırken aynen toplanır işaret artıdır(+) Eksi tam sayıyla eksi tam sayı toplanırken aynen toplanır işaret eksidir(-)
Zıt işaretli tam sayılar toplanırken birbirinden sayının önüne konur. Aynı işaretli tam sayıların çarpımı artıdır zıt işaretli tamsayıların çarpımı eksidir.
Sayı doğrsunda sağ tarafta bulunan sayı her zaman sol tarafta bulunan sayıdan daha büyüktür.
Sıfır tüm pozitif tam sayılardan küçük, tüm negatif tam sayılardan büyüktür.
NEgatif tam sayılarda büyük görünenler daha soldadır ve daha küçüktür.
Örneğin: -5 sayısı -6 sayısından büyüktür.
Örnek: -2,-1,+9,+4,0 Yandaki tam sayılar sıralayalım.
+9>+4>0>-1>-2
Örneğin; sayı doğrusu üzerinde bir +5 bir de -5 sayıları bulunmaktadır.
Bunlardan +5 sayısı sıfır sayısının sağında 5 birim uzaklıkta, -5 sayısı da sıfır sayısının solunda 5 birim uzaklıktadır.
birinin önünde -, diğerinin önünde + işareti var fakat her ikisi de 5 birim uzaklıkta.
Not: Uzaklık – ile ifade edilemez.
Örneğin Ahmet, Mehmet’ten -5 metre uzakta demeyiz. – sayısı bu durumlarda sadece yönümüzü belirtir.
Bir sayının önünde – varsa sıfırın solunda, + varsa sıfırın sağındadır.Biz sadece işaretlerden bunalrı anlarız.
Mutlak değer “| |” bu şeklin arasına sayı konarak gösterilir.
Örneğin: |+7| nin anlamı “+7 sayısı sıfırdan ne kadar uzaktadır” demektir.
Sonuç 7 birim uzaktadır olacaktır.
Örneğin: |-7| nin anlamı “-7 sayısı sıfırdan ne kadar uzaktadır” demektir.
Sonuç yine 7 birimdir.
Mutlak değer içine konan sayıların anlamı hiçbir zaman – olmaz.Çünkü uzaklıklar hiç – ile gösterilmez.
Bu durumda özetlersek;
|+7| = |-7| =7 olarak görülür.
Bütün sayılar için bunlar geçerlidir.
589 kere görüntülendi
6.Sınıf Matematik Tam Sayılar,Mutlak Değer Konu Anlatım Video (KastamonuMatematik.Com) from ibrahim tas on Vimeo.
Kastamonu Matematik | www.kastamonumatematik.com
DOĞAL SAYILAR NEDİR? (video)
Doğal sayılar, 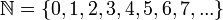 şeklinde sıralanan tam sayılardır. Negatif değer almazlar. Bazı kaynaklarda "0" doğal sayı olarak alınmaz. Matematikte hala sıfırın bir doğal sayı alınıp alınmayacağı tartışma konusudur, ancak eğer cebirsel inşâlar yapılmak isteniyorsa "0" sayısının doğal sayı olarak alınması avantaj sağlayabilir. Matematiğin diğer dallarında da problem hangi durumda daha kolay ifade edilebilecekse doğal sayılar kümesi de o şekilde alınır.
şeklinde sıralanan tam sayılardır. Negatif değer almazlar. Bazı kaynaklarda "0" doğal sayı olarak alınmaz. Matematikte hala sıfırın bir doğal sayı alınıp alınmayacağı tartışma konusudur, ancak eğer cebirsel inşâlar yapılmak isteniyorsa "0" sayısının doğal sayı olarak alınması avantaj sağlayabilir. Matematiğin diğer dallarında da problem hangi durumda daha kolay ifade edilebilecekse doğal sayılar kümesi de o şekilde alınır.
1) Birleşme Özelliği :19+36+4 işlemini yaparken önce 36 ile 4 ü toplayıp sonra 19 u eklemek daha kolaydır.Yani
19 + 36 + 4 = 19 + (36 + 4) = 19 + 40 = 59
Birleşme işlemi; en az üç sayı ile yapılan bir toplama işlemi düşünelim.Bu sayıları değişik sıralarla toplayalım.
Hangi sırayla toplarsak toplayalım işlemin sonucu değişmeyecektir.Buna birleşme işlemi denir.
Not: Parantezler hangi sayıları önce topladığımızı gösterir.
Örneğin;
(5+3)+7=8+7=15
5+(3+7)=5+10=15 görüldüğü gibi sonuç aynı
Aynısı çarpma işlemi için de geçerlidir.
(2.3).4=6.4=24
2.(3.4)=2.12=24 görüldüğü gibi sonuçlar aynı.
O halde birleşme özelliği vardır.
2) Değişme Özelliği
2 sayı toplanırken veya çarpılırken eyrleri değiştirildiğinde sonuç da değişmiyorsa, değişme özelliği vardır denir.
Buradan anladığımız şey şudur.
Sayıların yerlerini değiştireceğiz fakat sonuç değişmeyecek.
İnceleyelim.
8+7=15
7+8=15 ( sayıların yeri değişti fakat sonuç değişmedi)
9.10=90
10.9=90( sayıların yerleri değişti fakat sonuç aynı )
sayıların yeri değişti fakat sonuçları değişmedi.
Bu tür işlemlere değişme özelliği denir.
3) Dağılma Özelliği
Parantezin içinde toplama veya çıkarma işlemi, dışarıda da çarpma işlemi olduğunu düşünelim.
Örneğin; 6.(2+5) veya 9.(5-3)
Yukarıdaki gibi işlemlerde istersek önce parantez içini çözer, sonra dışarıdakiyle çarparız.
Veya, dışarıdakini içeridekilerle tek tek çarpar ve sonuçları ya toplarız, ya da çıkarırız.
Daha detaylı yapacak olursak, bir örnek üzerinden inceleyelim.
Örneğin;
204X6 yı kısa yolla çözelim
204 × 6 = 200×6 + 4×6 = 1,200 + 24 = 1,224
6.(2+5) burada önce 6 ile 2 yi çarparız, sonra yine 6 ile 5 i çarparız ve sonuçları toplarız ( arada toplama işareti olduğu için ).
Çözüm: 6.(2+5)=6.2+6.5=12+30=42 olarak sonuç bulunur.
Bir de 9.(5-3) işlemine bakalım.bu sefer 9 ile önce 5 i sonra 9 ile 3 ü çarpacağız fakat bu sefer sonuçları çıkartacağız ( arada çıkarma işlemi olduğu için )
9.(5-3)=9.5-9.3=45-27=18 olarak sonuç bulunur.
Toplama ve Çarpma işleminde 1 ile 0 ın etkisi
Bildiğiniz gibi 1 sayısı toplama işleminde sonucu değiştirir fakat çarpma işleminde değiştirmez.
Örneğin; 2+1=3 sonuç 2 den 3 e çıktı.
2.1=2 sonuç önceden de 2 idi, yine 2
Sıfır sayısı ise toplama işleminde sonucu değiştirmez ( etkisizdir) , çarpma işleminde ise sonucu değiştirir, sıfır yapar.Yani çarpma işleminde sıfır yutan elemandır.
Örneğin; 2+0=2 sonuç değişmedi.
2.0=0 sonuç sıfır oldu.

İşlem önceliği:
Birden çok işlem yan yana iken hangi sıra ile çözüm yapılır ?
Çözüm yapılırken rastgele sırayla ilerleyemeyiz, herşeyin bir sırası bulunmakta.
Örneğin;
15-2.5 işleminde önce çıkarma, sonra çarpma işlemi görünmekte fakat burada önce çarpma işlemini yapmalıyız.
Önce çıkarma işlemini yaparsak;
15-2.5=13.5=65 sonucu elde edilir.
Önce çarpma işlemi yapılırsa;
15-10=5 olarak sonuç bulunur.
ikincisi doğru sonuçtur.
peki;
(15-2).5 işlemine bakalım.
Burada ise parantez olduğu için önce çıkarma, sonra çarpma işlemi yapılır.
Yani;
13.5=65 doğru sonuçtur.
işlem önceliğinde; önce üslü sayılar yapılır,sonra parantez içlerine bakılır, ardından varsa çarpma veya bölme, daha sonra da toplama veya çıkarma işlemi yapılır.
Örnek Çözelim..
277 kere görüntülendi
6.Sınıf Matematik Doğal Sayılarda Toplama ve Çarpma Konu Anlatım Video (KastamonuMatematik.Com) from ibrahim tas on Vimeo.
Kastamonu Matematik | www.kastamonumatematik.com
186 kere görüntülendi
6.Sınıf Matematik Kümeler Video from Ali Hoca on Vimeo.







289 kere görüntülendi 6.Sınıf Matematik Doğru Parçası ve Işın Konu Anlatım Video (KastamonuMatematik.Com) from ibrahim tas on Vimeo.


361 kere görüntülendi
6.Sınıf Matematik Doğru Parçası ve Işın Konu Anlatım Video (KastamonuMatematik.Com) from ibrahim tas on Vimeo.
Kastamonu Matematik | www.kastamonumatematik.com
KONULAR :
KONULAR :
İKİZLER MATEMATİK DAHİSİ
Yedi yaşındaki sevimli ikizler, İngiltere’de A düzeyinde matemetik sınavını geçen en genç çocuklar oldu.
Daha yedi yaşındalar, ama başarıları koca profesörleri kıskandırıyor. Yedi yaşındaki bu sevimli ikizler, İngiltere’de A düzeyinde matemetik sınavını geçen en genç çocuklar oldu.
Peter ve Paula Imafidon adlı ikizler, yaklaşık 30 yıl önce İngiltere’ye yerleşmiş Nijeryalı bir ailenin çocukları. Ve bu ailenin ikizlerden önce de, ciddi başarılara imza atan üç kızı daha var.
En büyük kız kardeş Anne-Marie, A düzey bir bilgisayar sınavını geçen en genç insan olmuş daha 11 yaşındayken. Ortanca kardeş Samantha, çift A düzey matemetik diplomasıyla mezun olmuş liseden. Samantha ise yine A seviyeyle liseyi bitiren en genç isimlerden biriymiş.
Böyle başarılı ablaların kardeşi olan ikizler, Peter ve Paula ise not olarak istedikleri başarıyı yakalayamasalar da, yedi yaşında bu sınavı başarıyla veren en küçük çocuklar oldular.
Londra’nın doğusunda Walthamstow kasabasında yaşayan ikizler, devlet okuluna gidiyorlar ve ailelerinin durumu çok iyi değil. Bu yüzden de daha önce büyük başarılar kazanmış çocuklardan farklılar. Çünkü o çocuklar genelde aileleri ve özel öğretmenler tarafından evlerinde eğitim gören dahilerdi.
Maddi zorluklar çeken Chris ve Ann’in çocukları olan ikizler ise, gittikleri okul dışında bir vakıf olan Excellence in Education kurumunda ücretsiz eğitim alma hakkını da kazanmışlar. Bu kurum zeka seviyesi yüksek ve maddi durumu iyi olmayan çocuklara yardımcı olmaya çalışıyor.
MATEMATİKTE BAŞARI DA BAŞARISIZLIK DA GENETİK
ABD’de yapılan bir araştırma sayılarla ilgili doğuştan gelen duyarlılığın, matematik yeteneğine sahip olmada okulda alınan eğitimden daha önemli olduğunu ortaya çıkardı.
ABD’li bilim adamları matemetikte iyi olmanın, kişinin doğuştan sahip olduğu yeteneğe ve okula başlanan ilk yıllarda alınan eğitim olmak üzere iki faktöre bağlı olduğunu belirtirken, bu iki faktörün birbiriyle olan ilişkisini incelemek üzere bir araştırma yaptılar.
Maryland’de bulunan John Hopkins Üniversitesi araştırmacılarından Justin Halberda, yaptığı araştırmada yaşları 14 olan 64 çocuğa tahmini sayı algılama (ANS) adı verilen bir ölçüm testi yaptı. Seçilen çocukların hepsi geçmişte çok benzer matemetik eğitimi almış ve 5- 11 yaş arasında düzenli olarak matematik testlerine girmişti.
Halberda ve ekibi, katılımcılara bilgisayar ekranında yanıp sönen ışıklar gösterdi. Her ışık, mavi ve sarı renkte, 10-32 kez yanıp söndü. Deneklerden 200 milisaniyelik sürede akıllarında kalan renk ve yanıp sönen ışık sayısını söylemeleri istendi. Bazıları renkleri ve sayıları daha kolay algılayabilirken, bazıları da zorlandı. Tahminleri en yüksek seviyede yapan çocukların, zeka testlerinde en yüksek puan alan çocuklar olduğu ortaya çıktı. Halberda, deneklerin tümünün 5 yaşındayken, yani okula henüz başlamamış ve matematikle tanışmamışken IQ testine tabi tutulduklarını, testi başarıyla geçen çocukların IQ testlerinde en yüksek zeka seviyesine sahip olan çocuklar olduklarını belirtti.
Daha önce yapılan bir başka araştırmada da, bir Amazon kabilesinde eğitim görmemiş çocuklarla Fransa’da eğitim görmüş çocuklara ANS testi uygulanmış, iki grup arasında bariz bir fark olmadığı ortaya çıkmıştı.
Halberda, okulda görülen matematik derslerindeki başarı ya da başarısızlıkların büyük oranda genetiğe bağlı olduğunu söyledi. ABD’li araştırmacı ayrıca, ANS’nin güçlü bir test aracı olduğunu, buna rağmen yüzde 100 kesinliği olmadığını da sözlerine ekledi.
Matematikte somut örnek verme en iyi yöntem değil
ABD’de yapılan bir araştırmaya göre, matematik eğitimi sırasında somut örnekler vermek en iyi yöntem değil.Araştırmanın yapıldığı Ohio Eyalet Üniversitesinin tanımalı bilim merkezi müdürü Vladimir Sloutsky, "Matematiği somut bir örnekten yola çıkarak anlatmak çok zor. Somut örnekler, öğrenilenleri sınamak için iyi bir yöntem olabilir, ancak eğitim aracı olarak kötü yöntem" diye konuştu.
Amerikan Science dergisinin bugünkü sayısında yayımlanan araştırmaya göre, matematiği somut örneklerle öğrenen öğrenciler, soyut eğitim tarzıyla öğrenenlerle kıyaslandıklarında bunları yeni bir bağlamda kullanmakta sıkıntı çekiyorlar.Araştırmanın eşbaşkanlarından Jennifer Kaminski, soyut yöntem formülünü öğrenmedilerse "A treni B treni ile ne zaman karşılaşır?" sorusunu çözen öğrencilerin büyük bölümünün, bu çözümü diğer örneklere uygulamayamadıklarını belirtti.Teorilerini 4 gruba ayırdıkları 80 öğrenci üzerinde sınayan araştırmacılar, bir aritmetik sorusunun çözümünü ilk üç gruba ayrı ayrı 3 somut örnek vererek, dördüncü gruba da soyut anlatım tekniğiyle öğrettiler.Araştırmacılar daha sonra öğrettiklerini sınamak için çoktan seçmeli bir soruyu 80 öğrencinin tamamına sordular.Soyut yöntemle hesaplamayı öğrenenlerin yüzde 80’i doğru yanıt verirken, büyük bölümünün "kafadan atarak işlem yaptığı" diğer gruplarda sadece yüzde 43 ila yüzde 51 oranında doğru yanıt çıktı. Vladimir Sloutsky, somut örneklerin, öğrencilerin bizzat kavrama odaklanmalarına bile engel olabilecek biçimde ilgilerini dağıtabileceğini belirterek, araştırma sonuçlarının pedagojide uzun zamandır inanılanları tartışmaya açtığına işaret etti. Jennifer Kaminski de "Bu kavramları çok sembolik yöntemlerle anlatmak zorundayız. Öğrenciler böylece bunları çeşitli alanlara ygulamaya çok daha hazırlıklı olurlar" dedi.
Türk mühendisler 40 milyon bilinmeyenli denklemi çözdü 
Türk mühendisler 40 milyon bilinmeyenli denklemi çözdü Türk bilim adamları, İngiltere'den ödünç aldıkları bilgisayar sistemi ile en büyük integral problemini çözmeyi başardı. 40 milyon bilinmeyenli denklemin çözülmesinin sağlık ve savunma sanayiine katkı yapacağı belirtiliyor. Cep telefonlarının sağlığa etkisi de bu sayede tespit edilebilecek.
Yabancı meslektaşlarına kıyasla kısıtlı imkânlarla çalışan Türk bilim adamları, uluslararası bir başarıya imza attı. Bilkent Üniversitesi Bilişimsel Elektromanyetik Araştırma Merkezi (BiLCEM), tarihteki en büyük integral problemini çözerek dünya rekoru kırdı. Proje lideri Prof. Dr. Levent Gürel ve ekibi, yazılımını ve donanımını kendilerinin hazırladığı paralel bilgisayar sistemi ile 40 milyon bilinmeyenli bir denklemi çözdü. Bu sayede çok üst düzey modellemeler yapmanın mümkün olacağı ve simülasyon sistemi ile özellikle savunma ve sağlık sektörlerinde büyük aşama kaydedileceği belirtiliyor.
Projenin amaçlarından biri ise cep telefonlarının insan sağlığı üzerindeki etkilerini tespit etmek.Daha önce ABD'nin Illinois Üniversitesi'nde görevli bilim adamları en çok 22 milyon bilinmeyenli denkleme ulaşabilmişti. Rekor, alanında dünyanın en önemli kuruluşu Elektrik-Elektronik Mühendisleri Enstitüsü'nce haziran ayında bilim dünyasına duyurulacak. Başarının ilginç bir de öyküsü var: Yüksek kapasiteli bilgisayarlara ulaşma imkânı olmayan ekip, kendi ürettikleri yazılımlar ile bir paralelleme metodu oluşturdu ve INTEL firması ile temasa geçti. İngiltere'deki sistemini ödünç veren firma, çalışanlarının tatilde olduğu bir hafta sisteme Ankara'dan erişim sağladı. Hafta boyu süren aralıksız çalışma, rekoru da beraberinde getirdi.
Prof. Dr. Levent Gürel'in liderliğini yaptığı ve doktora öğrencisi Özgür Ergül ile Tahir Malas'tan oluşan BİLCEM ekibi, uzun süredir proje üzerine çalışıyordu. Kendi hazırladıkları yazılımlarla çok çekirdekli birden fazla bilgisayarı bir araya getirdiklerini kaydeden Levent Gürel, yaklaşık 250 gigabyte'lık bir hafıza kapasitesine ulaştıklarını dile getirdi. Bu kadar büyük hafızaya sahip bilgisayarların milyonlarca dolarlık maliyeti olduğunu hatırlatan ekip başkanı, kendi kullandıkları sistemin sadece 150 bin dolar değerinde olduğunu ifade etti.
Türk mühendisler tarafından geliştirilen çalışma, bilim dünyasında karşılaşılan büyük problemlere çözüm olabilecek nitelikte. Sistemin öncelikli olarak savunma ve sağlık sektörlerinde kullanılması hedefleniyor. Yüksek seviyeli elektromanyetik modelleme sistemi ile uçakların gelişmiş radar çözümlemeleri yapılabilecek, radara yakalanmayan uçak ve gemiler tasarlanabilecek.
Nano optik görüntüleme ile çok küçük partiküllerin incelenmesi sağlanabilecek. Çalışmanın en önemli amaçlarından biri ise cep telefonunun insan sağlığı üzerindeki etkilerini tespit edebilmek.
Bilkent Üniversitesi Elektrik Elektronik Mühendisliği Bölümü Başkan Yardımcısı Prof. Dr. Ergin Atalar da çözülen denklemin çok önemli olduğunu belirterek askerî ve sağlık alanında yapacağı katkılara dikkat çekti. Radar sistemlerinin bu çözümle daha detaylı bilgiler verebileceğini anlatan Atalar, "Uçağın büyüklüğünü ve modelini bile tespit edebilirler." diye konuştu. Projenin tıpta da kullanımının mümkün olduğunun altını çizen Prof. Dr. Ergin Atalar, cep telefonunun insan beynini kaç dakikada ne kadar ısıttığı ve bunun ne derece zararlı olduğu bilgisinin elde edilebileceğini dile getirdi.
7.sınıf öğrencisinden matematikte bir ilk
7. sınıf öğrencisi Mesut Şahin ardışık iki sayının karesini kullanarak ardışık 3. sayının karesinin hesaplanmasında geliştirdiği yöntemle ilgili hazırladığı proje Benim Eserim adlı proje yarışmasına kabul edildi.
Erzurum Kültür Kurumu İlköğretim Okulu 7. sınıf öğrencisi Mesut Şahin ardışık iki sayının karesini kullanarak ardışık 3. sayının karesinin hesaplanmasında geliştirdiği yöntemle ilgili hazırladığı proje Milli Eğitim Bakanlığının TÜBİTAK ile ortak yürüttüğü Benim Eserim adlı proje yarışmasına kabul edildi.
Şahin sayı karelerinin sırrı adlı projesinde 2 ardışık sayısının karesini kullanarak bu iki sayıdan sonra gelen üçüncü sayının karesinin bulunmasında yeni yöntem geliştirdi.
Proje danışmanı ve matematik öğretmeni İbrahim Baltacı öğrencisinin geliştirdiği yönteminin matematik literatüründe bulunmadığını ifade ederek Öğrencimiz başarılı bir çalışmaya imza attı. Onunla gurur duyuyoruz dedi.
Yarışmaya kabul edilen projenin önce bölge yarışmasına katılacağını anlatan Baltacı Proje bölge yarışmasında başarılı olursa ülke genelinde düzenlenecek yarışmaya katılmaya hak kazanacak diye konuştu.
Babası sınıf öğretmeni annesi ev hanımı olan Şahin rakamları çok sevdiğini belirterek Rakamlarla uğraşırken karelerinin bulunmasında yeni bir yöntem geliştirdim. Bununla ilgili proje hazırladım ve yarışmaya girdim dedi.
Doktor olmayı hedefleyen Şahin yaptığı çalışmayı şöyle anlattı;
Ardışık iki sayısın karelerini birbirinden çıkardıktan sonra iki ekliyoruz. Bu sayıyı iki ardışık sayıdan büyüğünün karesi topluyor 3. ardışık sayının karesini bulabiliyoruz. 3 ve 4 haneli rakamlarda da aynı işlemi yaptım ve başarılı oldum. Tüm pozitif sayılarda bu yöntem kullanılabilir.
Dünya matematik yarışmasında birinci Türkler oldu
Kocaeli'nde eğitim veren Özel Erkul İlköğretim Okulu öğrencileri, 180 bin yarışmacının katıldığı Dünya Matematik Olimpiyatı'nda altın madalya almayı başardı.
Ahmet Güneri, İrem Narman ve Kadir Aslantaş'tan oluşan matematik olimpiyat takımı Türkiye'ye madalya kazandırmış olmanın mutluluğunu yaşıyor. 6. sınıftan itibaren bu yarışmaya hazırlanan öğrenciler yoğun bir çalışma programının ardından gelen birinciliğin sevincini şu sözlerle dile getiriyor: "3 yıldır birlikte aynı takım arkadaşları ile çalışıyoruz. 6. sınıfta başladığımız olimpiyatların 3 yıl sonra karşılığını alıyoruz.
Hedefimiz geleceğin bilim adamları olmak ve Amerika'da aldığımız bu başarıya paralel NASA gibi bir kurumun Türkiye'de bulunmasını sağlamak ve ülkemizde bu çalışmaları yapmaktır." Amerika'nın dışında Singapur 6, Kanada 5, Çin 2, Honk Kong 1, Filipinler 1 ve Guam Adaları 1 madalya kazandı. Amerika Birleşik Devletleri'nde bulunan Nebraska Üniversitesi tarafından yapılan ve dünyanın en prestijli yarışması olarak kabul edilen İlköğretim Okulları Dünya Matematik Olimpiyatı'nın (AMC-8) bu yıl 22'ncisi düzenlendi. İnternet üzerinde yapılan yarışmaya dünya genelinde 180 bin öğrenci katıldı. Türkiye'den de çok sayıda öğrencinin katıldığı yarışma sonuçlandı. Sonuçlara göre Türkiye'de bir tek Özel Erkul İlköğretim Okulu altın madalya aldı. Okulun başarısını kutlayanlar arasında Milli Eğitim Bakanı Hüseyin Çelik de yer aldı. Altın madalya alan öğrenci ve öğretmenleri dün makamında kabul eden Çelik, "Geleceğin Türkiye'sini kuracak olan siz değerli gençlerin bilgiyi uygulamaya dökmenizi istiyorum." dedi.
Bu yıl 22.si düzenlenen AMC-8'de okul puanları, yarışmaya katılan 3 öğrencinin doğru cevap toplamına göre hesaplanıyor. Öğrencilere 25 adet soru soruluyor ve 66 ile 75 puan arasındaki okullara ödül veriliyor. Türkiye'den yarışmaya katılan okullar arasında Özel Erkul İlköğretim Okulu öğrencileri, 66 puanı bularak altın madalya almayı başardı.
Özel Erkul İlköğretim Okulu Matematik Olimpiyatı koordinasyon sorumlusu Kıvanç Yanık, öğrencilerle uzun süredir olimpiyatlara hazırlandıklarını söyledi. Alınan bu başarının kendilerine yeni başarı yolunda güç vereceğini ifade eden Yanık, "Öğrencilerimiz 6. sınıfta ilköğretim müfredatını bitirdiler, 7. sınıfta ise lise müfredatını bitirdiler ve ilköğretimde çıkmış olimpiyat sorularını çözdüler. Bundan sonra da ulusal ve uluslararası düzeydeki yarışmalarda öğrencilerimizin başarısı için yoğun bir çalışma programı ile hazırlıklarımız devam edecektir." dedi.
Erkekler matematikte kızlardan iyi değilmiş!
Science dergisinde yayınlanan bir haber, matematikte erkeklerin kızlardan daha iyi olduğuna dair genel kanıyı yalanladı.Oldukça yaygın bir kanaat olan kadınların çoğunun bilim ve teknoloji alanlarında kariyer yapacak donanımlarının olmadığı kanısının aksine, ikinci sınıftan on birinci sınıfa kadar 7 milyondan fazla öğrenciden edinilen test sonuçlarının analizine göre kız ve erkek öğrencilerin matematik puanları arasında herhangi belirgin bir farka rastlanmadı.
Bu çalışma aynı zamanda erkeklerin matematik dehası olmaya kızlardan daha yatkın oldukları varsayımını da sarstı. Araştırma sonuçlarına göre, en yüksek puana ulaşan yüzde 5'lik grupta erkek öğrenciler kadar kızlar da yer aldı.
Araştırmayı yöneten Wisconsin üniversitesinden Psikolog Janet Hyde "Hem aileler hem de öğretmenler matematikte erkeklerin kızlardan daha iyi olduğu yargısını taşımaya devam ediyor." dedi ve ekledi: "Bence bu yargı tam olarak doğru değil."
Hyde ve meslektaşları 2005 ve 2007 yılları arasındaki matematik testlerinin sonuçlarını ayrıntılı olarak incelediler.
Araştırmacılar, California ve diğer dokuz eyaletteki kızlar ve erkeklerin ortalama puanlarını karşılaştırarak hiç bir eyalette kızların ya da erkeklerin belirgin bir üstünlüğü olmadığı sonucuna vardılar.
Sorular karmaşık muhakeme yeteneklerini ölçmeye yönelik tasarlanmış olduğu halde, cinsiyetler arasındaki farklılıklar ihmal edilebilir düzeyde kaldı.
Araştırmaya katılmamış olan Claremont McKenna College'dan psikoloji profesörü Diane Halpern " Bu verilerde kızların matematikte başarılı olamayacağına dair hiçbir şey yok". diye konuştu. Halpern, ayrıca kızların ders müfradatından elde edilmiş testlerde daha iyi puanlar aldığını belirtti.
Doksanlı yıllarda yapılan çalışmalarda erkek ve kız öğrencilerin ilk okulda matematik testlerinde eşit puanlar alırken liseye gelindiğinde erkeklerin kompleks problemler içeren testlerde kızları geride bırakmaya başladığı tespit edilmişti.
Hyde, seçkin üniversitelere girebilme kaygısının kızları üst düzey matematik dersleri almaya itmiş olmasını, doksanlı yıllarlada yapılmış testler ile günümüzde yapılan testlerin sonuçları arasında ortaya çıkan bu farklılığın bir sebebi olabileceğini düşünüyor.
Pi Sayısı 6. basamakta değişiyor, 15. basamakta kendisini takip ediyor.
Türk Matematikçi Kerim Sarılar; "Pi Sayısı 6. basamakta değişiyor. 15. basamakta kendisini takip ediyor" dedi.
Matematik ve Geometri Teorisyeni Kerim Sarılar, Elektronik Haber Ajansı (e-ha)'ya; Pi Sayısı ile ilgili İlginç açıklamalarda bulundu. Pi Sayısı 6. basamakta değişiyor. 15. basamakta kendisini takip ediyor.
Çemberin Çevresinin Çapına Oranı 6. basamakta değişiyor mu? 15. basamaktan sonra kendini mi takip ediyor?
"3,1415930986402531415930986403"
Dairenin çevresinin çapına bölümü ile elde edilen ve bu gün dünyaca kabul gören Pi sayısının 6. basamakta değiştiğini ifade eden SARILAR;."Biz 2004 yılında test işlemlerini tamamlayarak ürettiğimiz Süper Çizim ve Süper Ölçüm Programı ile ilgili 2004 yılında TÜBİTAK ve Ondokuz Mayıs Üniversitesinden "Gözlem Raporu" talep ettik.
"Süper Çizim ve Süper Ölçüm" programımız üzerinde bu gün dünyaca kabul gören Pi sayısını kullandık. Ancak daha sonra yazılım kodlarından bazılarını kaldırarak hesaplamalarımızı yapmaya çalıştık ve ürettiğimiz yatay elipsin, dikey elipsin çevresinin çapına bölümü ile elde edilen Pi sayısının 6. basamakta değiştiğine şahit olduk.
Yatay Elips İçin;
Pi = Çember veya Yatay Elipsin Çevresi. / (AB + ( AB * (Alan oranı)))
Dikey Elips İçin;
Pi = Çember veya Dikey Elipsin Çevresi. / (AB + ( AB / (Alan oranı)))
formüllerimizde elde ettiğimiz 3,1415930986404421169999999999 sayı Orta Doğu Teknik Üniversitesinin 20.11.2007 tarih ve B.30.2.ODT.0.13.00.00/211/07/3021 - 016814 sayılı yazısı ve eki raporda da yer aldığı üzere; "Eserde elektronik çizim ve hesaplama yöntemlerinden yararlanıldığı anlaşılmaktadır. Bu tür yöntemlerin ve bu yöntemlerin uygulandığı cihazların irrasyonel sayısal sayılarla işlem yapmaları mümkün olmadığından belli bir "yaklaşıklık kabulü" ile işlem yapmaları kaçınılmazdır. Nitekim, elde edilen sayıya da bu minval yol takip edilerek ulaşıldığı." İfade edilmişti.
Ancak AR - GE çalışmalarına devam ettim. Ar - Ge çalışmalarımızda önce yaklaşık değer olarak kabul ettiğim : 3,14159309864025 ve sonra 3,1415930986402531415930986403 sayıya ulaşarak Pi sayısının 15. basamaktan itibaren kendini takip ettiğine şahit olduk. Ancak yatay elipsin çevresinin çapına bölümü ile elde edilen 3,14159309864025 sayı kalıcı kök teşkil etti. Çünkü hafıza kodu bu sayıya kadar işlem yapıyordu.
Kendisinin bulduğu bu üç farklı sayının yazılım dilinde işlem yaparken kullandığı hafıza kodlarından kaynaklandığını ifade eden Türk Matematikçi Kerim SARILAR; bütün Pi sayısı tariflerinde çemberin çevresinin çapına bölümü ile elde edilen sayı olarak tanımlanmaktadır. Oysa bizim ürettiğimiz yatay ve dikey elips formüllerinde de görüleceği üzere dikey elipsin çevresinin çapına, yatay elipsin çevresinin çapına oranı da diyebiliriz dedi.
Eser ve AR - GE çalışmalarının ülkemizde desteklenmediğini ifade eden SARILAR; bunun nedeninin de eser ve Ar - Ge çalışmalarının desteklenmesi ile ilgili yönetmeliklerin fikri mülkiyet kanunu dahilinde hazırlanmaması ve çıkartılmaması olduğunu ifade etti. Ülkemizin bazı Üniversitelerinde eser üretme ile ilgili fikri mülkiyet kanununa göre hazırlanmış politikaların bulunmadığına işaret eden Türk Matematikçi Sayın Kerim SARILAR; "Bu alanda büyük bir boşluk bulunmaktadır. Öncelikle üretilmiş bir eseri inceleyen Öğretim Üyelerine belli bir ücret ödenmelidir. Öğretim üyesine incelediği eserle ilgili gerek teknik ve gerekse hukuka uygunluğu yönünden yükselmede ek puan verilmelidir. Devletin bu işlemleri yapması dahi eserin desteklenmesine katkı sağlar. Ülkemizin önü açılır" dedi.
Pi = Çember veya Yatay Elipsin Çevresi. / (AB + ( AB * (Alan oranı)))
Pi = Çember veya Yatay Elipsin Çevresi. / (AB + ( AB * (2 * çevre oranı - 1)))
Yine kendi geliştirdiği Pi bulma formülü ile de Pi = 3,14159309864025 sayısına ulaştı.
Pi = ((Çember veya Yatay Elipsin Çevresi. / (( AB + AB* Alan oranı )))
Alan Oranı = 1 olduğunda çember; Alan Oranı < 1 olduğunda Yatay elipstir.
Pi = ((Yatay Elipsin Çevresi. / (( AB + AB* Alan oranı )))
Pi = ((395,84073042867189584073042868 / (( 70 + 70 * 0,8)))
Pi = 3,1415930986402531415930986403
Alan oranı = 1
Yarıçap = AB = 100
Çembere Girilen Açı = 60
AD = 50
DC = 86,6025403784439
Pi = 3,14159309864025
Kosinüs değeri = AD * 180 / (AB * Açı * Pi)
Kosinüs değeri = 50 * 180 / (100 * 60 * 3,14159309864025 )
Kosinüs değeri = 0,477464761636137
Sinüs değeri = DC * 180 / ( AB * Alan oranı * Açı * Pi)
Sinüs değeri = 86,6025403784439 * 180 / ( 100 * 1 * 60 * 3,14159309864025)
Sinüs değeri = 0,826993225977552
Ç Cos A = (Kosinüs değeri * Açı * Pi) / 180
Ç Cos A = (0,477464761636137 * 60 * 3,14159309864025 ) / 180
Ç Cos A = 0,5
Ç Sin A = (Sinüs değeri * Açı * Pi ) / 180
Ç Sin A = (0,826993225977552 * 60 * 3,14159309864025 ) / 180
Ç Sin A = 0,866025403784439
Pi = (Ç Cos A * 180) / (Kosinüs değeri * Açı)
Pi = (0,5 * 180) / (0,477464761636137 * 60 )
Pi = 3,14159309864025
Pi = (Ç Sin A * 180 ) / (Sinüs değeri * Açı )
Pi = (0,866025403784439 * 180 ) / (0,826993225977552 * 60)
Pi = 3,141593098640